【PyTorch学习笔记】8.对抗生成网络

根据龙良曲Pytorch学习视频整理，视频链接：
【计算机-AI】PyTorch学这个就够了！
(好课推荐)深度学习与PyTorch入门实战——主讲人龙良曲

52.GAN简介

生成式对抗网络(Generative Adversarial Nets)是一种无监督深度学习模型，通过生成模型（Gererative Model）和判别模型（Discriminative Model）的互相博弈学习产生相当好的输出。一般捕获数据分布的G和估计样本来自训练数据概率的D都是深度神经网络。判别模型需要输入变量，通过某种模型来预测。生成模型是给定某种隐含信息，来随机产生观测数据。

53.画家的成长历程

GAN 主要包括了两个部分，即生成器G (generator)与判别器D (discriminator)

1. G通过接收一个随机噪声z生成图片，记作G(z)。G主要用来学习真实图像分布从而让自身生成的图像更加真实，以骗过判别器
2. D的输入参数是x，输出D(x)代表x为真实图片的概率。判别器则需要对接收的图片进行真假判别

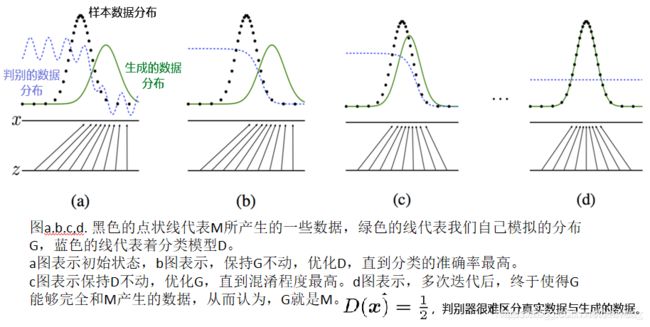
对于给定的真实图片（real image），判别器要为其打上标签 真1；对于给定的生成图片（fake image），判别器要为其打上标签 假0；对于生成器传给辨别器的生成图片，生成器希望辨别器打上标签 1。随着时间推移，生成器和判别器不断地进行对抗，最终两个网络达到了一个动态均衡：生成器生成的图像接近于真实图像分布，而判别器识别不出真假图像，对于给定图像的预测为真的概率基本接近 0.5（相当于随机猜测类别），即$D(G(z))=0.5$。

损失函数
$mi{n}_{G}ma{x}_L(D,G)=E_{x\sim p_r(x)}[logD(x)]+E_{z\sim p_z(z)}[log(1-D(G(z)))]$
$=E_{x\sim p_r(x)}[logD(x)]+E_{x\sim p_g(x)}[log(1-D(x))]$

54.纳什均衡

首先介绍一下KL散度、JS散度和交叉熵。三者都是用来衡量两个概率分布之间的差异性的指标。

KL散度（Kullback–Leibler Divergence）：又称KL距离，相对熵。当概率分布P(x)和Q(x)的相似度越高，KL散度越小。KL散度主要有两个性质：

1. 不对称性：尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即$D(P||Q)\ne D(Q||P)$
2. 非负性：相对熵的值是非负值，即$D(P||Q)>0$
   $$D_{KL}(p||q)={\int }_{x}p(x)log\frac{p(x)}{q(x)}dx$$

JS散度（Jensen-Shannon Divergence）：又称JS距离，是KL散度的一种变形。不同于KL主要有两方面：

1. 值域范围：JS散度的值域范围是[0,1]，相同则是0，相反为1。相较于KL，对相似度的判别更确切了
2. 对称性：即 $JS(P||Q)=JS(Q||P)$
   $$D_{JS}(p||q)=\frac{1}{2}{D}_{KL}(p||\frac{p+q}{2}+\frac{1}{2}{D}_{KL}(q||\frac{p+q}{2})$$

交叉熵（Cross Entropy）：在神经网络中交叉熵可作为损失函数，因为它可以衡量P和Q的相似性$$H(P,Q)=\sum P(x)log\frac{1}{Q(x)}$$

交叉熵和相对熵的关系：$$D(P||Q)=H(P,Q)-H(P)$$

54.1纳什均衡-D

Q1. Where will D converge, given fixed G?

54.2纳什均衡-G

Q2, Where will G converge, after optimal D?

训练最好的情况时$p_r=p_g$，此时$L(G,D^{\ast })=2log2$

55.JS散度的弊端

通常GAN在训练的时候会出现不稳定，因为在大多数情况，$P_G$和$P_{data}$是不重叠的（overlapped）:

1. The nature of data：Both $P_G$ and $P_{data}$ are low-dimanifold in high-dim space. The overlap can be ignored.
2. Sampling：Even though $P_G$ and $P_{data}$ have overlap. If you do not have enough sampling…

如果$P_G$和$P_{data}$不重叠，$D_{KL}=+\infty$, $D_{JS}=log2$

Gradient Vanishing

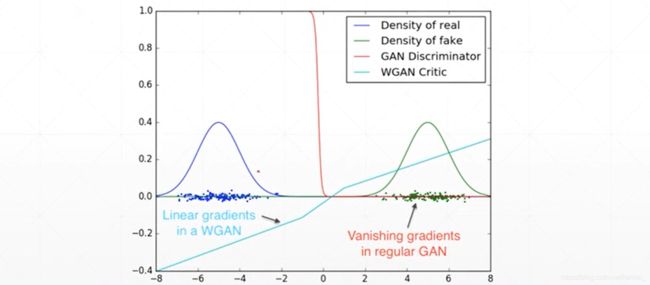
Traing Progress Invisible

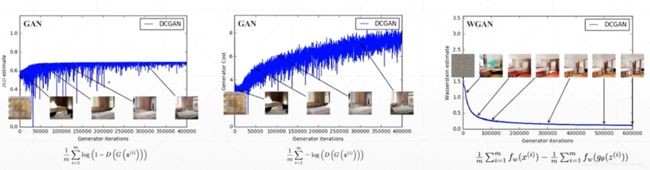
56.EM距离

WGAN可以解决以上问题，其引入了EM距离

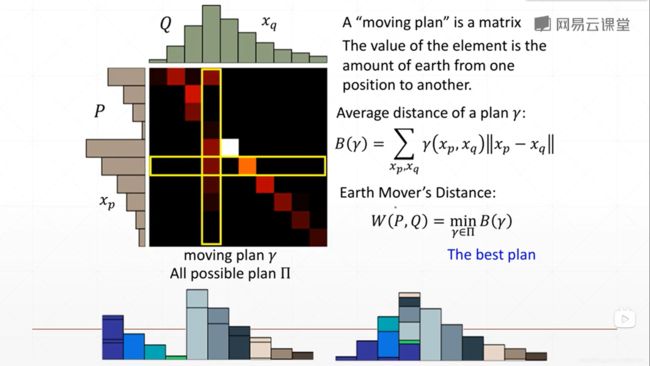
How to compute Wasserstein Distance?

离散情况下Wasserstein Distance可以很好解决overlapped问题，连续情况如果f函数满足1-Lipschitz function，Discriminator就能模拟Wasserstein Distance，训练就会稳定。Weight Clipping是实现1-Lipschitz function的一种方式：

57.WGAN与WGAN-GP

WGAN-GP可以很好解决1-Lipschitz function问题

事实证明WGAN-GP可以训练更稳定，虽然DCGAN的训练结果更好，但是DCGAN需要精心设计网络和参数等，相较来说WGAN-GP是最佳选择

58.实战

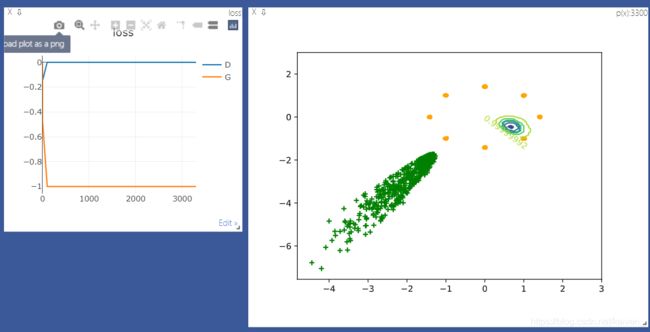
58.1GAN

import torch
from torch import nn, optim, autograd
import numpy as np
import visdom
import random
import matplotlib.pyplot as plt

h_dim = 400
batchsz = 512
viz = visdom.Visdom()

class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()

        self.net = nn.Sequential(
            # z:[b, 2] => [b, 2]
            nn.Linear(2, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, 2),
        )

    def forward(self, z):
        output = self.net(z)
        return output

class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()

        self.net = nn.Sequential(
            nn.Linear(2, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, 1),
            nn.Sigmoid()
        )

    def forward(self, x):
        output = self.net(x)
        return output.view(-1)

def data_generator():
    """
    8-gaussian mixture models
    :return:
    """
    scale = 2
    centers = [
        (1, 0),
        (-1, 0),
        (0, 1),
        (0, -1),
        (1. / np.sqrt(2), 1. / np.sqrt(2)),
        (1. / np.sqrt(2), -1. / np.sqrt(2)),
        (-1. / np.sqrt(2), 1. / np.sqrt(2)),
        (-1. / np.sqrt(2), -1. / np.sqrt(2))
    ]
    centers = [(scale * x, scale * y) for x, y in centers]

    while True:
        dataset = []
        for i in range(batchsz):
            point = np.random.randn(2) * 0.02
            center = random.choice(centers)
            # N(0, 1) + center x1/x2
            point[0] += center[0]
            point[1] += center[1]
            dataset.append(point)

        dataset = np.array(dataset).astype(np.float32)
        dataset /= 1.414
        yield dataset

def generate_image(D, G, xr, epoch):
    """
    Generates and saves a plot of the true distribution, the generator, and the critic
    :param D:
    :param G:
    :param xr:
    :param epoch:
    :return:
    """
    N_POINTS = 128
    RANGE = 3
    plt.clf()   # 清除当前 figure 的所有axes，但是不关闭这个 window，所以能继续复用于其他的 plot。

    points = np.zeros((N_POINTS, N_POINTS, 2), dtype='float32')
    points[:, :, 0] = np.linspace(-RANGE, RANGE, N_POINTS)[:, None]
    points[:, :, 1] = np.linspace(-RANGE, RANGE, N_POINTS)[None, :]
    print('p:', points.shape)   # p: (128, 128, 2)
    points = points.reshape((-1, 2))
    print('p:', points.shape)   # # (16384, 2)

    # draw contour
    with torch.no_grad():
        points = torch.Tensor(points).cuda()    # [16384, 2]
        disc_map = D(points).cpu().numpy()      # [16384, ]
    x = y = np.linspace(-RANGE, RANGE, N_POINTS)
    cs = plt.contour(x, y, disc_map.reshape((len(x), len(y))).transpose())
    plt.clabel(cs, inline=1, fontsize=10)    

    # draw samples
    with torch.no_grad():
        z = torch.randn(batchsz, 2).cuda()  # [b, 2]
        samples = G(z).cpu().numpy()    # [b, 2]
    plt.scatter(xr[:, 0], xr[:, 1], c='orange', marker='.')
    plt.scatter(samples[:, 0], samples[:, 1], c='green', marker='+')

    viz.matplot(plt, win='contour', opts=dict(title='p(x):%d'%epoch))


def main():
    torch.manual_seed(23)
    np.random.seed(23)

    data_iter = data_generator()
    x = next(data_iter)
    # [b, 2]
    # print(x.shape)  # (512, 2)

    G = Generator().cuda()
    D = Discriminator().cuda()
    # print(G)
    # print(D)
    optim_G = optim.Adam(G.parameters(), lr=5e-4, betas=(0.5, 0.9))
    optim_D = optim.Adam(D.parameters(), lr=5e-4, betas=(0.5, 0.9))

    viz.line([[0, 0]], [0], win='loss', opts=dict(title='loss', legend=['D', 'G']))

    for epoch in range(50000):
        # 1. train Discrimator firstly
        for _ in range(5):
            # 1.1 train on real data
            xr = next(data_iter)
            xr = torch.from_numpy(xr).cuda()
            # [b, 2] => [b, 1]
            predr = D(xr)
            # max predr
            lossr = -predr.mean()

            # 1.2 train on fake data
            # [b, ]
            z = torch.randn(batchsz, 2).cuda()
            xf = G(z).detach()  # tf.stop_gradient()
            predf = D(xf)
            lossf = predf.mean()

            # aggregate all
            loss_D = lossr + lossf

            # optimize
            optim_D.zero_grad()
            loss_D.backward()
            optim_D.step()

        # 2. train Generator
        z = torch.randn(batchsz, 2).cuda()
        xf = G(z)
        predf = D(xf)
        # max gredf.mean()
        loss_G = -predf.mean()

        # optimize
        optim_G.zero_grad()
        loss_G.backward()
        optim_G.step()

        if epoch % 100 == 0:
            viz.line([[loss_D.item(), loss_G.item()]], [epoch], win='loss', update='append')

            print(loss_D.item(), loss_G.item())

            generate_image(D, G, xr.cpu(), epoch)


if __name__ == '__main__':
    main()

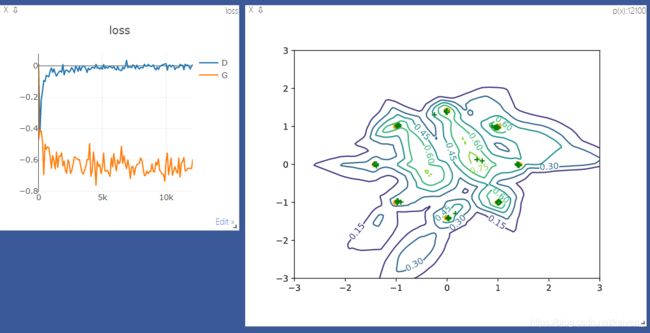
58.2WGAN

def gradient_penalty(D, xr, xf):
    """
    :param D:
    :param xr: [b, 2]
    :param xf: [b, 2]
    :return:
    """
    # [b, 1]
    t = torch.rand(batchsz, 1).cuda()
    # [b, 1] => [b, 2]
    t = t.expand_as(xr)
    # interpolation
    mid = t * xr + (1 - t) * xf
    # set it requires gradient
    mid.requires_grad_()

    pred = D(mid)
    grads = autograd.grad(outputs=pred, inputs=mid,
                          grad_outputs=torch.ones_like(pred),
                          create_graph=True, retain_graph=True, only_inputs=True)[0]

    gp = torch.pow(grads.norm(2, dim=1) - 1, 2).mean()
    return gp

...

			# 1.3 gradient penalty
            gp = gradient_penalty(D, xr, xf.detach())

            # aggregate all
            loss_D = lossr + lossf + 0.2*gp