PYthon 教你怎么选择SVM的核函数kernel及案例分析
关注微信公共号:小程在线
![]()
关注CSDN博客:程志伟的博客
4种核函数的适用场景
接上文可以选在非线性核函数,可以将数据明显的区别开
clf = SVC(kernel = "rbf").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
H:\Anaconda3\lib\site-packages\sklearn\svm\base.py:193: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
"avoid this warning.", FutureWarning)
#################探索核函数在不同数据集上的表现################
1. 导入所需要的库和模块
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
2. 创建数据集,定义核函数的选择
n_samples = 100
datasets = [
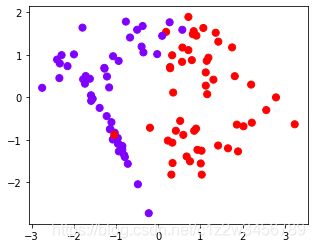
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
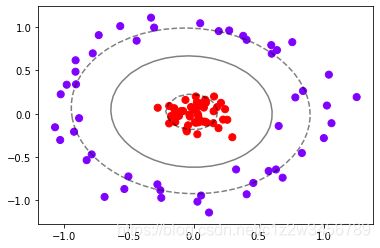
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_blobs(n_samples=n_samples, centers=2, random_state=5),
make_classification(n_samples=n_samples,n_features =
2,n_informative=2,n_redundant=0, random_state=5)
]
Kernel = ["linear","poly","rbf","sigmoid"]
for X,Y in datasets:
plt.figure(figsize=(5,4))
plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
以上4张图分别是月牙形,环形,杂乱性,对称形
我们总共有四个数据集,四种核函数,我们希望观察每种数据集下每个核函数的表现。以核函数为列,以图像分布
为行,我们总共需要16个子图来展示分类结果。而同时,我们还希望观察图像本身的状况,所以我们总共需要20
个子图,其中第一列是原始图像分布,后面四列分别是这种分布下不同核函数的表现
3. 构建子图
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(20,16))
4. 开始进行子图循环
#第一层循环:在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
#在图像中的第一列,第一个,放置原数据的分布
#zorder=10表示画布的层级,edgecolors表示边缘额颜色
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data")
ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
ax.set_xticks(())
ax.set_yticks(())
#第二层循环:在不同的核函数中循环
#从图像的第二列开始,一个个填充分类结果
for est_idx, kernel in enumerate(Kernel):
#定义子图位置,从第一列,第二个开始
ax = axes[ds_cnt, est_idx + 1]
#建模
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
score = clf.score(X, Y)
#绘制图像本身分布的散点图
ax.scatter(X[:, 0], X[:, 1], c=Y
,zorder=10
,cmap=plt.cm.Paired,edgecolors='k')
#绘制支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=50,
facecolors='none', zorder=10, edgecolors='k')
#绘制决策边界
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
#np.mgrid,合并了我们之前使用的np.linspace和np.meshgrid的用法
#一次性使用最大值和最小值来生成网格
#表示为[起始值:结束值:步长]
#如果步长是复数,则其整数部分就是起始值和结束值之间创建的点的数量,并且结束值被包含在内
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
#np.c_,类似于np.vstack的功能
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
#填充等高线不同区域的颜色
ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
#绘制等高线
ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
levels=[-1, 0, 1])
#设定坐标轴为不显示
ax.set_xticks(())
ax.set_yticks(())
#将标题放在第一行的顶上
if ds_cnt == 0:
ax.set_title(kernel)
#为每张图添加分类的分数
ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
, size=15
, bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
#为分数添加一个白色的格子作为底色
, transform=ax.transAxes #确定文字所对应的坐标轴,就是ax子图的坐标轴本身
, horizontalalignment='right' #位于坐标轴的什么方向
)
plt.tight_layout()
plt.show()
__main__:53: UserWarning: No contour levels were found within the data range.
可以观察到,线性核函数和多项式核函数在非线性数据上表现会浮动,如果数据相对线性可分,则表现不错,如果
是像环形数据那样彻底不可分的,则表现糟糕。在线性数据集上,线性核函数和多项式核函数即便有扰动项也可以
表现不错,可见多项式核函数是虽然也可以处理非线性情况,但更偏向于线性的功能。
Sigmoid核函数就比较尴尬了,它在非线性数据上强于两个线性核函数,但效果明显不如rbf,它在线性数据上完全
比不上线性的核函数们,对扰动项的抵抗也比较弱,所以它功能比较弱小,很少被用到。rbf,高斯径向基核函数基本在任何数据集上都表现不错,属于比较万能的核函数。
#########################探索核函数的优势和缺陷###########################
通过绘制SVC在不同核函数下的决策边界并计算SVC在不同核函数下分类准确率来观察核函数的效用
1. 导入所需要的库和模块
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from time import time
import datetime
data = load_breast_cancer()
X = data.data
y = data.target
X.shape
Out[3]: (569, 30)
np.unique(y)
Out[4]: array([0, 1])
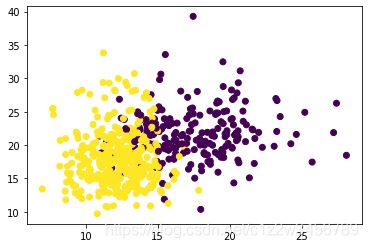
plt.scatter(X[:,0],X[:,1],c=y)
plt.show()
from sklearn.decomposition import PCA
X_dr = PCA(2).fit_transform(X)
X_dr.shape
Out[6]: (569, 2)
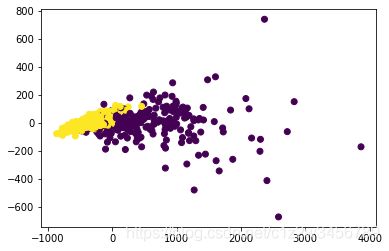
plt.scatter(X_dr[:,0],X_dr[:,1],c=y)
plt.show()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
#下面的代码运行不出来
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
# , degree = 1
, cache_size=5000 #内存
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
模型一直停留在线性核函数之后,就没有再打印结果了。这证明,多项式核函数此时此刻要消耗大量的时间,运算非常的缓慢
#时间戳
time()
Out[9]: 1585731238.5509906
now = time()
datetime.datetime.fromtimestamp(now).strftime("%Y-%m-%d,%H:%M:%S:%f")
Out[10]: '2020-04-01,16:56:35:263156'
在循环中去掉多项式核函数
Kernel = ["linear","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
# , degree = 1
, cache_size=5000 #内存
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
The accuracy under kernel linear is 0.929825
00:00:926657
The accuracy under kernel rbf is 0.596491
00:00:084060
The accuracy under kernel sigmoid is 0.596491
00:00:010509
乳腺癌数据集是一个线性数据集,线性核函数跑出来的效果很好。rbf和sigmoid两个擅长非线性的数据从效果上来看完全不可用。其次,线性核函数的运行速度远远不如非线性的两个核函数。如果数据是线性的,那如果我们把degree参数调整为1,多项式核函数应该也可以得到不错的结果。
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
, degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
The accuracy under kernel linear is 0.929825
00:00:823586
The accuracy under kernel poly is 0.923977
00:00:157116
The accuracy under kernel rbf is 0.596491
00:00:078048
The accuracy under kernel sigmoid is 0.596491
00:00:010008
多项式核函数的运行速度立刻加快了,并且精度也提升到了接近线性核函数的水平,rbf在线性数据上也可以表现得非常好,那在这里,为什么跑出来的结果如此糟糕呢?其实,这里真正的问题是数据的量纲问题。回忆一下我们如何求解决策边界,如何判断点是否在决策边界的一边?是靠计算”距离“,虽然我们不能说SVM是完全的距离类模型,但是它严重受到数据量纲的影响。让我们来探索一下乳腺癌数据集的量纲
import pandas as pd
data = pd.DataFrame(X)
data.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T
Out[13]:
count mean std ... 90% 99% max
0 569.0 14.127292 3.524049 ... 19.530000 24.371600 28.11000
1 569.0 19.289649 4.301036 ... 24.992000 30.652000 39.28000
2 569.0 91.969033 24.298981 ... 129.100000 165.724000 188.50000
3 569.0 654.889104 351.914129 ... 1177.400000 1786.600000 2501.00000
4 569.0 0.096360 0.014064 ... 0.114820 0.132888 0.16340
5 569.0 0.104341 0.052813 ... 0.175460 0.277192 0.34540
6 569.0 0.088799 0.079720 ... 0.203040 0.351688 0.42680
7 569.0 0.048919 0.038803 ... 0.100420 0.164208 0.20120
8 569.0 0.181162 0.027414 ... 0.214940 0.259564 0.30400
9 569.0 0.062798 0.007060 ... 0.072266 0.085438 0.09744
10 569.0 0.405172 0.277313 ... 0.748880 1.291320 2.87300
11 569.0 1.216853 0.551648 ... 1.909400 2.915440 4.88500
12 569.0 2.866059 2.021855 ... 5.123200 9.690040 21.98000
13 569.0 40.337079 45.491006 ... 91.314000 177.684000 542.20000
14 569.0 0.007041 0.003003 ... 0.010410 0.017258 0.03113
15 569.0 0.025478 0.017908 ... 0.047602 0.089872 0.13540
16 569.0 0.031894 0.030186 ... 0.058520 0.122292 0.39600
17 569.0 0.011796 0.006170 ... 0.018688 0.031194 0.05279
18 569.0 0.020542 0.008266 ... 0.030120 0.052208 0.07895
19 569.0 0.003795 0.002646 ... 0.006185 0.012650 0.02984
20 569.0 16.269190 4.833242 ... 23.682000 30.762800 36.04000
21 569.0 25.677223 6.146258 ... 33.646000 41.802400 49.54000
22 569.0 107.261213 33.602542 ... 157.740000 208.304000 251.20000
23 569.0 880.583128 569.356993 ... 1673.000000 2918.160000 4254.00000
24 569.0 0.132369 0.022832 ... 0.161480 0.188908 0.22260
25 569.0 0.254265 0.157336 ... 0.447840 0.778644 1.05800
26 569.0 0.272188 0.208624 ... 0.571320 0.902380 1.25200
27 569.0 0.114606 0.065732 ... 0.208940 0.269216 0.29100
28 569.0 0.290076 0.061867 ... 0.360080 0.486908 0.66380
29 569.0 0.083946 0.018061 ... 0.106320 0.140628 0.20750
[30 rows x 13 columns]
数据存在严重的量纲不一的问题。我们来使用数据预处理中的标准化的类,对数据进行标准化
from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X)
data = pd.DataFrame(X)
data.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T
Out[14]:
count mean std ... 90% 99% max
0 569.0 -3.162867e-15 1.00088 ... 1.534446 2.909529 3.971288
1 569.0 -6.530609e-15 1.00088 ... 1.326975 2.644095 4.651889
2 569.0 -7.078891e-16 1.00088 ... 1.529432 3.037982 3.976130
3 569.0 -8.799835e-16 1.00088 ... 1.486075 3.218702 5.250529
4 569.0 6.132177e-15 1.00088 ... 1.313694 2.599511 4.770911
5 569.0 -1.120369e-15 1.00088 ... 1.347811 3.275782 4.568425
6 569.0 -4.421380e-16 1.00088 ... 1.434288 3.300560 4.243589
7 569.0 9.732500e-16 1.00088 ... 1.328412 2.973759 3.927930
8 569.0 -1.971670e-15 1.00088 ... 1.233221 2.862418 4.484751
9 569.0 -1.453631e-15 1.00088 ... 1.342243 3.209454 4.910919
10 569.0 -9.076415e-16 1.00088 ... 1.240514 3.198294 8.906909
11 569.0 -8.853492e-16 1.00088 ... 1.256518 3.081820 6.655279
12 569.0 1.773674e-15 1.00088 ... 1.117354 3.378079 9.461986
13 569.0 -8.291551e-16 1.00088 ... 1.121579 3.021867 11.041842
14 569.0 -7.541809e-16 1.00088 ... 1.123053 3.405812 8.029999
15 569.0 -3.921877e-16 1.00088 ... 1.236492 3.598943 6.143482
16 569.0 7.917900e-16 1.00088 ... 0.882848 2.997338 12.072680
17 569.0 -2.739461e-16 1.00088 ... 1.117927 3.146456 6.649601
18 569.0 -3.108234e-16 1.00088 ... 1.159654 3.834036 7.071917
19 569.0 -3.366766e-16 1.00088 ... 0.904208 3.349301 9.851593
20 569.0 -2.333224e-15 1.00088 ... 1.535063 3.001373 4.094189
21 569.0 1.763674e-15 1.00088 ... 1.297666 2.625885 3.885905
22 569.0 -1.198026e-15 1.00088 ... 1.503553 3.009644 4.287337
23 569.0 5.049661e-16 1.00088 ... 1.393000 3.581882 5.930172
24 569.0 -5.213170e-15 1.00088 ... 1.276124 2.478455 3.955374
25 569.0 -2.174788e-15 1.00088 ... 1.231407 3.335783 5.112877
26 569.0 6.856456e-16 1.00088 ... 1.435090 3.023359 4.700669
27 569.0 -1.412656e-16 1.00088 ... 1.436382 2.354181 2.685877
28 569.0 -2.289567e-15 1.00088 ... 1.132518 3.184317 6.046041
29 569.0 2.575171e-15 1.00088 ... 1.239884 3.141089 6.846856
[30 rows x 13 columns]
再次运行核函数
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
, degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
The accuracy under kernel linear is 0.976608
00:00:016012
The accuracy under kernel poly is 0.964912
00:00:006004
The accuracy under kernel rbf is 0.970760
00:00:013005
The accuracy under kernel sigmoid is 0.953216
00:00:007990
量纲统一之后,可以观察到,所有核函数的运算时间都大大地减少了,尤其是对于线性核来说,而多项式核函数居
然变成了计算最快的。其次,rbf表现出了非常优秀的结果。经过我们的探索,我们可以得到的结论是:
1. 线性核,尤其是多项式核函数在高次项时计算非常缓慢
2. rbf和多项式核函数都不擅长处理量纲不统一的数据集
选取与核函数相关的参数:degree & gamma & coef0
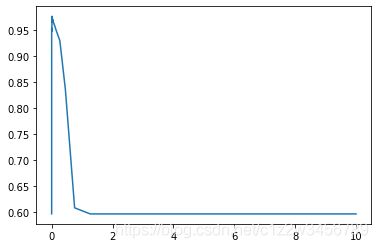
对于高斯径向基核函数,调整gamma的方式其实比较容易,那就是画学习曲线。我们来试试看高斯径向基核函数
rbf的参数gamma在乳腺癌数据集上的表现
score = []
gamma_range = np.logspace(-10, 1, 50) #返回在对数刻度上均匀间隔的数字
for i in gamma_range:
clf = SVC(kernel="rbf",gamma = i,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), gamma_range[score.index(max(score))])
plt.plot(gamma_range,score)
plt.show()
0.9766081871345029 0.012067926406393264
通过学习曲线,很容就找出了rbf的最佳gamma值。但我们观察到,这其实与线性核函数的准确率一模一样之前的
准确率。我们可以多次调整gamma_range来观察结果,可以发现97.6608应该是rbf核函数的极限了。
但对于多项式核函数来说,一切就没有那么容易了,因为三个参数共同作用在一个数学公式上影响它的效果,因此
我们往往使用网格搜索来共同调整三个对多项式核函数有影响的参数。依然使用乳腺癌数据集
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV
time0 = time()
gamma_range = np.logspace(-10,1,20)
coef0_range = np.linspace(0,5,10)
param_grid = dict(gamma = gamma_range
,coef0 = coef0_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=420)
grid = GridSearchCV(SVC(kernel = "poly",degree=1,cache_size=5000),
param_grid=param_grid, cv=cv)
grid.fit(X, y)
print("The best parameters are %s with a score of %0.5f" % (grid.best_params_,grid.best_score_))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
The best parameters are {'coef0': 0.0, 'gamma': 0.18329807108324375} with a score of 0.96959
00:16:152746
网格搜索为我们返回了参数coef0=0,gamma=0.18329807108324375,但整体的分数是0.96959,虽然比调参前略有提高,但依然没有超过线性核函数核rbf的结果。可见,如果最初选择核函数的时候,就发现多项式的结果不如rbf和线性核函数