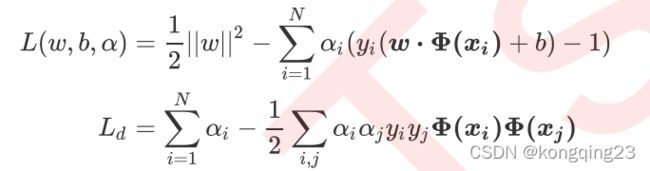机器学习sklearn-支持向量机2

目录

非线性SVM和核函数

如何选择最佳核函数

SVC在乳腺癌数据上的表现

---

非线性SVM和核函数

非线性 SVM 的损失函数的初始形态为：

同理，非线性 SVM 的拉格朗日函数和拉格朗日对偶函数也可得：

这种变换非常巧妙，但也带有一些实现问题。 首先，我们可能不清楚应该什么样的数据应该使用什么类型的映射函数来确保可以在变换空间中找出线性决策边界。极端情况下，数据可能会被映射到无限维度的空间中，这种高维空间可能不是那么友好，维度越多，推导和计算的难度都会随之暴增。其次，即使已知适当的映射函数，我们想要计算类似于点积，计算量可能会无比巨大，要找出超平面所付出的代价是非常昂贵的。

而解决这些问题的数学方式，叫做 “ 核技巧”(Kernel Trick)，是一种能够使用数据原始空间中的向量计算来表示升维后的空间中的点积结果的数学方式。具体表现为

 而这个原始空间中的点积函数 ，就被叫做“核函数”(Kernel Function)。

 

 

可以看出，除了选项 "linear" 之外，其他核函数都可以处理非线性问题。多项式核函数有次数 d ，当 d 为 1 的时候它就是再处理线性问题，当d 为更高次项的时候它就是在处理非线性问题。我们之前画图时使用的是选项 “linear" ，自然不能处理环形数据这样非线性的状况。

如何选择最佳核函数

我们通过一个例子，来探索一下不同数据集上核函数的表现。我们现在有一系列线性或非线性可分的数据，我们希望通过绘制SVC 在不同核函数下的决策边界并计算 SVC 在不同核函数下分类准确率来观察核函数的效用。

 以上4张图分别是月牙形，环形，杂乱性，对称形

我们总共有四个数据集，四种核函数，我们希望观察每种数据集下每个核函数的表现。以核函数为列，以图像分布为行，我们总共需要16个子图来展示分类结果。而同时，我们还希望观察图像本身的状况，所以我们总共需要20个子图，其中第一列是原始图像分布，后面四列分别是这种分布下不同核函数的表现。

 

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles,make_moons,make_blobs,make_classification

n_samples=100
#生成4种不同类型数据 月牙形 环形 杂乱形 对称形
data=[
    make_moons(n_samples=n_samples,noise=0.2,random_state=0),
    make_circles(n_samples=n_samples,noise=0.2,factor=0.5,random_state=1),
    make_blobs(n_samples=n_samples,centers=2,random_state=2),
    make_classification(n_samples=n_samples,n_features=2,n_informative=2,#特征数 带特征的有两个
                        n_redundant=0,random_state=3) #不带特征的0个 即不存在需要舍去的特征
]

#核函数列表
Kernel = ["linear","poly","rbf","sigmoid"]
# #查看4个数据集分布
# for X,Y in data:
#     plt.figure(figsize=(5,4))
#     plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
#     plt.xticks([])
#     plt.yticks([])

#构建子图
nrows=len(data)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(20,16))
#子图循环
#第一层循环：在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(data):
    # 在图像中的第一列，放置原数据的分布
    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Input data")
    ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired, edgecolors='k')#zorder指定层级
    ax.set_xticks(())
    ax.set_yticks(())

    # 第二层循环：在不同的核函数中循环
    # 从图像的第二列开始，一个个填充分类结果
    for est_idx, kernel in enumerate(Kernel):
        #定义子图位置 从每一行从1列到4列
        ax=axes[ds_cnt, est_idx+1]
        #建模
        clf=svm.SVC(kernel=kernel,gamma=2).fit(X, Y)
        score=clf.score(X, Y)

        #绘制图像散点图
        ax.scatter(X[:, 0], X[:, 1], c=Y, zorder = 10,
                   cmap = plt.cm.Paired, edgecolors = 'k')
        #绘制支持向量
        ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=50,
                   facecolors = 'none', zorder = 10, edgecolors = 'k') #facecolor表示透明 避免覆盖
        #绘制决策边界
        #加减0.5 避免点落在边界上
        x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
        y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
        # np.mgrid，合并了我们之前使用的np.linspace和np.meshgrid的用法
        # 一次性使用最大值和最小值来生成网格
        # 表示为[起始值：结束值：步长]
        # 如果步长是复数，则其整数部分就是起始值和结束值之间创建的点的数量，并且结束值被包含在内
        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        # np.c_，类似于np.vstack的功能
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
        # 填充等高线不同区域的颜色
        ax.pcolormesh(XX, YY, Z > 0, shading='auto',cmap=plt.cm.Paired)
        # 绘制等高线
        ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
                   levels = [-1, 0, 1])

        # 设定坐标轴为不显示
        ax.set_xticks(())
        ax.set_yticks(())
        # 将标题放在第一行的顶上
        if ds_cnt == 0:
            ax.set_title(kernel)

        # 为每张图添加分类的分数
        ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0'), #0.95 0.06横纵坐标 lstrip表示不显示0
                size = 15, bbox = dict(boxstyle='round',
                alpha=0.8, facecolor='white'),
        # 为分数添加一个白色的格子作为底色
        transform = ax.transAxes, # 确定文字所对应的坐标轴，就是ax子图的坐标轴本身
        horizontalalignment = 'right',)  # 位于坐标轴的什么方向


plt.tight_layout()#自动调整子图大小
plt.show()

SVC在乳腺癌数据上的表现

from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime

data = load_breast_cancer()
X = data.data
y = data.target
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

Kernel = ["linear","rbf","sigmoid"] #多项式核函数跑不出来
for kernel in Kernel:
    time0=time()
    clf=SVC(kernel=kernel,gamma='auto',cache_size=5000).fit(Xtrain,Ytrain) #cache_size 为内存 MB
    print("The accuracy under kernel {} is {}".format(kernel, clf.score(Xtest,Ytest)))
    print(datetime.datetime.fromtimestamp(time() - time0).strftime("%M:%S:%f")) #分 秒 微秒

尝试对数据进行标准化后 

from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime

data = load_breast_cancer()
X = data.data
y = data.target
X = StandardScaler().fit_transform(X)#标准化数据
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

Kernel = ["linear","poly","rbf","sigmoid"] #多项式核函数跑不出来
for kernel in Kernel:
    time0=time()
    clf=SVC(kernel=kernel,gamma='auto',cache_size=5000).fit(Xtrain,Ytrain) #cache_size 为内存 MB
    print("The accuracy under kernel {} is {}".format(kernel, clf.score(Xtest,Ytest)))
    print(datetime.datetime.fromtimestamp(time() - time0).strftime("%M:%S:%f")) #分 秒 微秒

量纲统一之后，可以观察到，所有核函数的运算时间都大大地减少了，尤其是对于线性核来说，而多项式核函数居然变成了计算最快的。其次，rbf 表现出了非常优秀的结果。经过我们的探索，我们可以得到的结论是：

1. 线性核，尤其是多项式核函数在高次项时计算非常缓慢

2. rbf 和多项式核函数都不擅长处理量纲不统一的数据集

幸运的是，这两个缺点都可以由数据无量纲化来解决。因此， SVM 执行之前，非常推荐先进行数据的无量纲化！