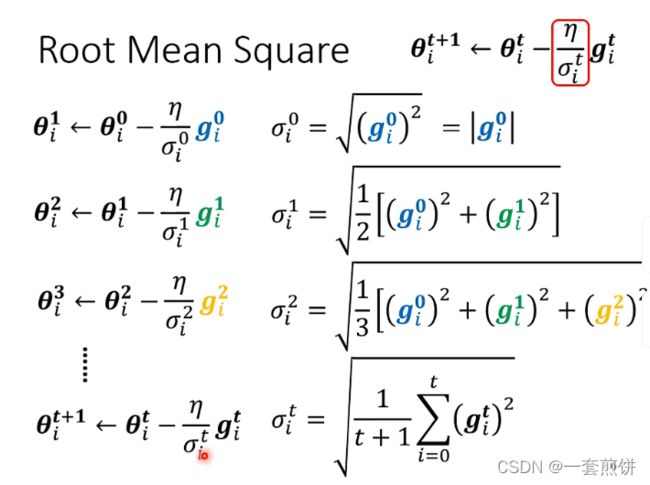（10）-3类神经网络训练不起来怎么办？

critical point 不一定是训练当中最大的障碍，今天讲的是Adaptive Learning Rate（自适应学习率）的技术。

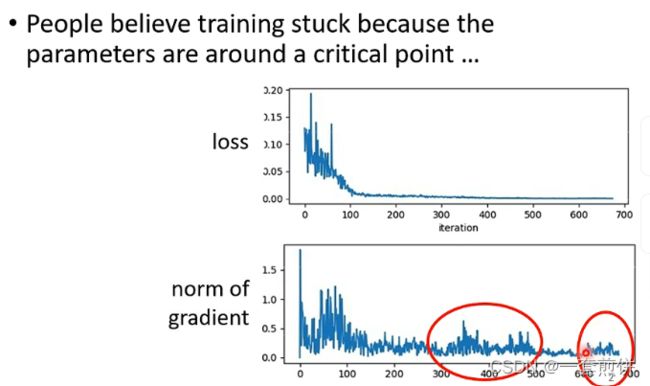
当loss函数随着参数的更新的时候，遇到critical point时loss不再更新，此时的gradient非常小，但是有确认过当loss不在下降的时候，gradient真的很小吗？

从上面的这个图可以看出虽然loss不在下降，但是gradient的大小没有真的变得很小，出现这样的情况的原因是什么呢？

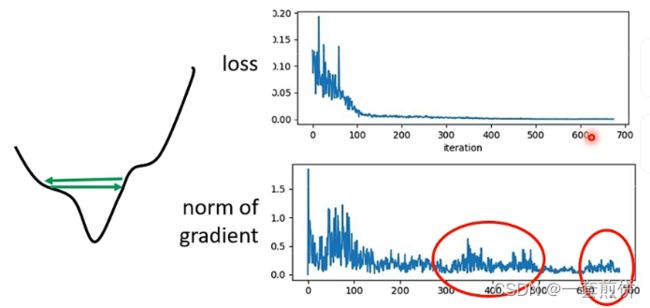
根据error surface可以知道，gradient在error surface山谷的两个谷壁之间来回的震荡，此时的loss不在下降，实际上卡到critical point吗？不是的，他的gradient仍然很大，只是loss不见得减小了。

总结来说：当loss随着参数的更新不再下降的时候，不一定是卡在critical point或者是local minima处。只是单纯的loss没有办法降下来。

为什么我们在训练的时候会卡住呢？排除掉不是critical point的原因。

举例说明：(如下图)

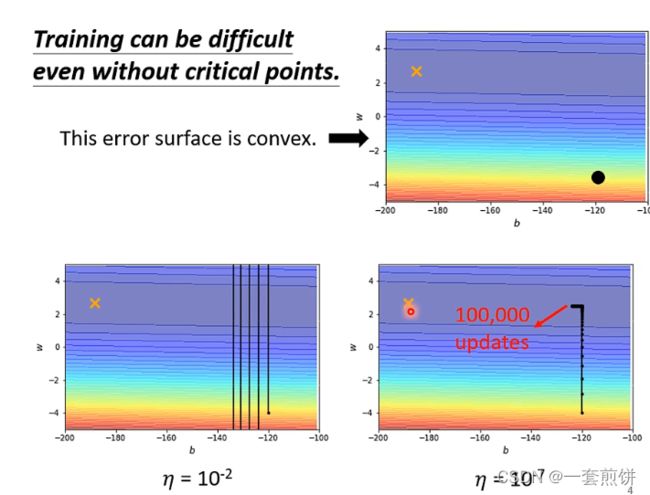
这个error surface是一个convex的形状，他的最低点再x点处。这个convex的形状是他的等高线是椭圆形状的，只是在横轴的地方他的gradient非常小，坡度变化的很小，非常的平滑，所以椭圆的长轴非常的长，短轴相对之下非常的短，纵轴的时候变化很大，error surface的坡度非常的陡峭。

现在我们从图中黑色的点（初始的点）来做gradient descent。

当learning rate是10的-2次方的时候，参数再峡谷的两端不断地震荡，loss就没办法下降，但是此时的gradient是很大的，learning rate大的话就是参数很大，所以loss就没法滑倒山谷里面，但是讲learning rate很小的时候，就不再震荡了，划到了山谷底，但是这个训练时走不到头的。是因为learning rate太小了。所以说即使是一个convex的error surface也是很难用gradient descent去训练的。

 我们现在怎么样把gradient descent做的更好呢？以前用的是将learning设的一样的值，但是这样做是远远不够的，learning rate要为每一个参数设不同的数值。不应该是一刀切的。

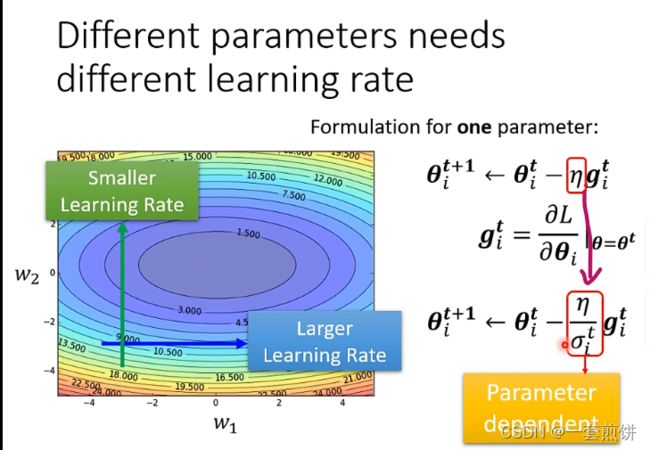
不同的参数需要不同的learning rate

如果在某一个方向上gradient的值很小，在某一个方向上非常的平缓，我们希望learning rate调大一点，如果在某一个方向上非常的陡峭，可以让learning rate小一点。那么learning rate如何根据gradient的大小做调整呢？我们要改一下gradient原来的式子。（现在只看一个参数的，但是可以推广到所有的参数）

 

现在我们看这个新的learning rate有什么常见的计算方式

root mean square

最常见的方式是计算gradient的root mean square（ 均方根）

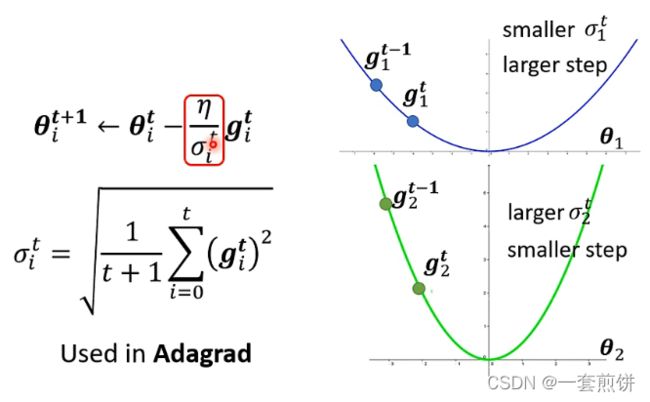
 上面的这个方法可以用在Adagrad中，

 在这个参数比较小的时候，计算的loss就比较小，那么gradient也是小的，因为和gradient有关系，所以也小，learning rate就大。反之，则小。（下面的这个绿色的图像）

所以有了这一项就可以根据gradient的大小来自动调整learning rate的大小。

但是上面的这个结论也不是最终我们想要的。

另一种方法是：

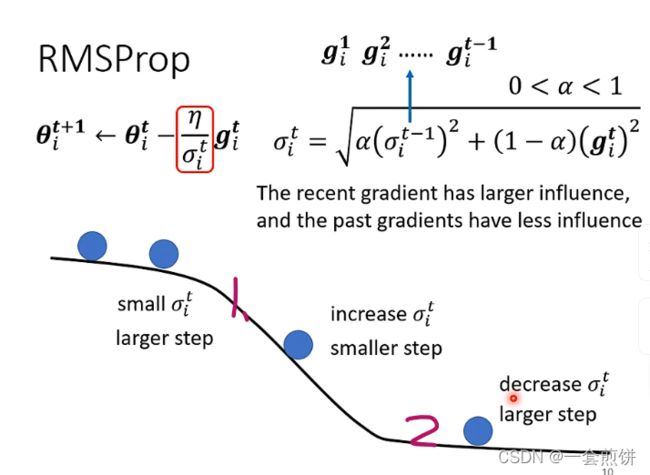
RMSProp

其中的是可以自己调整的

 

 从第一个蓝色的球到第二个蓝色的球，error surface很平坦，g就算出的很小，代表说很小，在更新参数的时候就迈出很大的一步，到第三个球，此时的gradient就变得很大了，如果我们用RMSProp的话，把设得小一点，此时的就增大了，那迈出的步伐就小一点，把Learing rate变小。

现在最常用的优化策略是：

Adam：RMSProp+Momentum

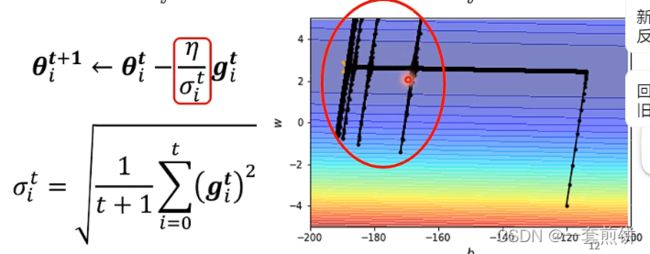
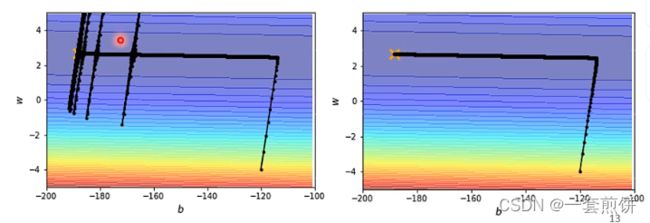
 现在用上面的这中方法来看一下：

 但是为什么会出现红圈当中爆炸的情况呢？

是因为在此之前积累了很多的gradient比较的小的数值，所以积累了一定的程度之后，gradient就会突然的爆炸，会出现暴增的情况，此时的gradient的值很大，但是gradient很大的时候，就会变得很大，learning rata就会变得很小，参数的更新的距离就会必须变小，暴增的部分就会被修正。

 怎么解决上面出现的情况？

Learning rata Scheduling（两种方法）

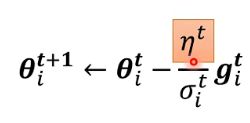是固定的值，但是是跟时间有关的，就是随着时间的不断进行，不断减小。此时的Learing rata就不断的减小。

第一种方法：learning rata decay

 

 为什么让learning rata减小呢？

因为一开始我们距离终点很远，随着参数的不断更新，我们距离终点越来越近，所以把Lear ing rata减小，让我们的参数有了一个急刹车。

 左边的情况加上一个learning ratadecay就会出现右边的情况，不会出现突然的暴增。

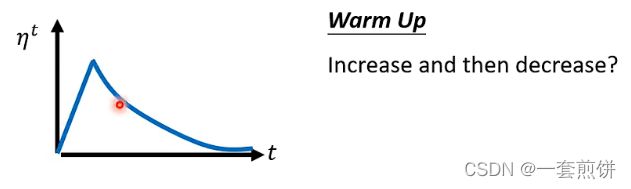
另一种方法是：Warm up

就是learning rata先变大后变小的情况

 先搜集的统计情况，在让learning rata慢慢的爬升

warm up 专门的文章：

总结：

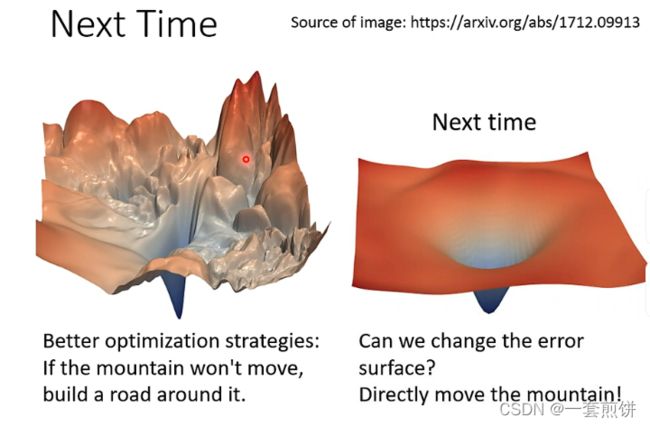
我们现在讲的问题是：当error surface特别崎岖的时候，我们需要比较好的方法去做优化问题

 借来将的问题是讲崎岖不平的error surface通过什么样的方法变平。