力扣解题思路:队列与栈 纠错记录
232. 用栈实现队列
思路:由于队列是先进先出,栈是先进后出,所以要用栈实现队列只能使用两个栈,因为执行一次出栈和入栈之后栈元素的顺序就会正好相反,所以再取出的peek就是队头啦~~
class MyQueue {
private Stack<Integer> in = new Stack<>();
private Stack<Integer> out = new Stack<>();
public void push(int x) {
in.push(x);
}
public int pop() {
in2out();
return out.pop();
}
public int peek() {
in2out();
return out.peek();
}
private void in2out() {
if (out.isEmpty()) {
while (!in.isEmpty()) {
out.push(in.pop());
}
}
}
public boolean empty() {
return in.isEmpty() && out.isEmpty();
}
}
只要out一直不为空,out中的值就一直是队头。
225. 用队列实现栈
思路:由于队列出队再入队之后队列中的元素也会是一样的顺序,所以用过两个队列来实现栈实属没必要,所以只用一个队列就可以啦。由于队列先出来的是队头元素, 那么如何获取队尾元素呢?我们可以把除队尾的其他元素出队再入队一遍,那么对尾不就是队头了么o(  ̄▽ ̄)ブ,悄咪咪说一句,其实LinkedList本身是可以既充当队列也充当栈的,但是初始化的时候需要写成LinkedList<> stack = new LinkedList<>()啦~
接下来我们看代码:
class MyStack {
private Queue<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) {
queue.add(x);
int cnt = queue.size();
while (cnt-- > 1) {
queue.add(queue.poll());
}
}
public int pop() {
return queue.remove();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}
是不是很简单~~
155. 最小栈
思路:这一题我一直认为是个比较简单的题,甚至比上面两个简单多了,用栈来实现栈还不简单吗?于是我使用两个栈,其中一个用来保存数据,另一个用来维护最小值:
class MinStack {
public Stack<Integer> a = new Stack<>();
public Stack<Integer> b = new Stack<>();
/** initialize your data structure here. */
public MinStack() {
}
public void push(int x) {
if(a.isEmpty()){
a.push(x);
b.push(x);
}else{
a.push(x);
if(x<=b.peek()){
b.push(x);
}
}
}
public void pop() {
if(a.peek().equals(b.peek())){
a.pop();
b.pop();
}else{
a.pop();
}
}
public int top() {
return a.peek();
}
public int getMin() {
return b.peek();
}
}
这里需要提醒的一点是,千万不要把a.peek().equals(b.peek())写成了a.peek() == b.peek(), 我枯了,一开始的时候我就写的a.peek() == b.peek()一直找不到错误在哪,后来才发现这个,记住==比较的是两个地址值!即使数值一样,地址值也是可能不一样的(对于Integer和int都是!),测试用例中有出现-1024、512等超过正常int数值范围的数值,因此转integer即自动装箱时会比较地址值而不是数值!!(正常范围时-128到127之间),所以要用equals比较值!
还有另外一个比较简单的方法,再用个min维护最小值,就不需要一直比较栈顶的值啦~
class MinStack {
private Stack<Integer> dataStack;
private Stack<Integer> minStack;
private int min;
public MinStack() {
dataStack = new Stack<>();
minStack = new Stack<>();
min = Integer.MAX_VALUE;
}
public void push(int x) {
dataStack.add(x);
min = Math.min(min, x);
minStack.add(min);
}
public void pop() {
dataStack.pop();
minStack.pop();
min = minStack.isEmpty() ? Integer.MAX_VALUE : minStack.peek();
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
还可以这样写,更容易理解:
public MinStack() {
stack = new Stack<Integer>();
}
public void push(int x) {
if(stack.isEmpty()){
stack.push(x);
stack.push(x);
}else{
int tmp = stack.peek();
stack.push(x);
if(tmp<x){
stack.push(tmp);
}else{
stack.push(x);
}
}
}
public void pop() {
stack.pop();
stack.pop();
}
public int top() {
return stack.get(stack.size()-2);
}
public int getMin() {
return stack.peek();
}
这样比较简单是因为两个栈总是同时入栈和出栈,能保持一致。ヾ(≧▽≦*)o
面试题 03.05. 栈排序
思路:
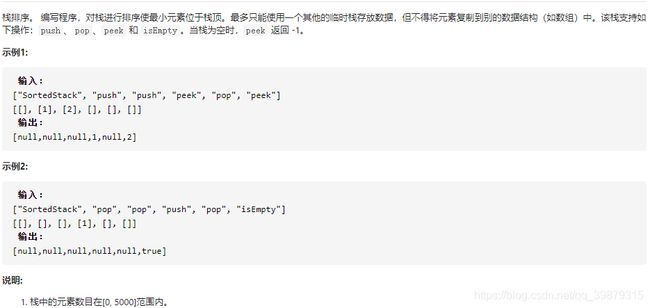
这题和 232. Implement Queue using Stacks 还有 implements stack using Queues 以及 Min Stack。 思考的切入角度都是一样的。 具体地, 就是采用增量法。就比如这题。 你假设你的 主stack已经是满足sorted stack 的 性質了。 我们需要思考的就是当你来一个新的元素的时候, 怎么借用辅助栈/队列,来维持这个性质,。 对于这个题目,就是你需要将比它大的元素先放到辅助栈中,然后把目标值存入主栈中, 然后 再把辅助栈的元素放回来(插入排序思想):
class SortedStack {
Deque<Integer> minStack; // 维护一个单调递增(sort in acending)/递减栈(sort in decending),栈顶最大
Deque<Integer> tempStack; // 辅助栈(栈能保证顺序,所以不可以用队列,不过如果是双端队列,那就当我没说)
public SortedStack() {
minStack = new LinkedList<>();
tempStack = new LinkedList<>();
}
public void push(int val) {
while (!minStack.isEmpty() && minStack.peek() < val) {
tempStack.push(minStack.pop());
}//找到比当前数val小的位置,在他上面放入val,再把临时保存在辅助栈中的元素放上来
minStack.push(val);
while (!tempStack.isEmpty()) {
minStack.push(tempStack.pop());
}
}
public void pop() {
if (isEmpty()) {
return;
}
minStack.pop();
}
public int peek() {
if (isEmpty()) {
return -1;
}
return minStack.peek();
}
public boolean isEmpty() {
return minStack.isEmpty();
}
}
剑指 Offer 59 - II. 队列的最大值
思路:
这个题目与上面类似,但是实际上不可以用最大栈的思想,先看我的错误代码吧:
class MaxQueue {
// 使用单调队列记录最大值即可
LinkedList<Integer> maxQ;
Queue<Integer> q;
public MaxQueue() {
maxQ = new LinkedList<Integer>();
q = new LinkedList<Integer>();
}
public int max_value() {
if (maxQ.isEmpty()) {
return -1;
}
return maxQ.peekLast();
}
public void push_back(int value) {
if(q.isEmpty()){
q.add(value);
maxQ.add(value);
}else{
q.add(value);
if(maxQ.peekLast()<value){
maxQ.add(value);
}else{
maxQ.add(maxQ.peekLast());
}
}
}
public int pop_front() {
if (q.isEmpty()) {
return -1;
}
int res = q.poll();
maxQ.poll();
return res;
}
}
举个例子,如果按照321入队列,那么此时maxQ应该是333,但是如果这是移除3,maxQ应该是33,那这就错了!!!!这是因为栈只有一个出入口,而队列则不是。
解决办法:
// 使用单调队列记录最大值即可
Deque<Integer> maxQ;
Queue<Integer> q;
public MaxQueue() {
maxQ = new LinkedList<Integer>();
q = new LinkedList<Integer>();
}
public int max_value() {
if (maxQ.isEmpty()) {
return -1;
}
return maxQ.peekLast();
}
public void push_back(int value) {
q.offer(value);
while ((!maxQ.isEmpty()) && maxQ.peekFirst() < value) {
maxQ.pollFirst();
}
maxQ.offerFirst(value);
}
public int pop_front() {
if (q.isEmpty()) {
return -1;
}
int res = q.poll();
if (res == maxQ.peekLast()) {
maxQ.pollLast();
}
return res;
}
另外一个队列采用头插法,如果对头比它小,就将对头出队直到遇到比它大的,然后入队,那我们每次返回的最大值就是队尾(队尾最大,整个队列从前往后是递增的)。那么poll时要检查poll出的元素是否是最大队列的尾部第一个(尾部第一个是最大的),如果是则尾部出队,如果不是证明该元素早就出队了,不可能还存在于最大队列中!!
如果做过剑指 Offer 59 - I. 滑动窗口的最大值
会发现其实这一题也可以用一样的思路,也就是往队尾添加元素,对头来保持最大元素:
class MaxQueue {//和上一题思路类似
// 使用单调队列记录最大值即可
Deque<Integer> maxQ;
Queue<Integer> q;
public MaxQueue() {
maxQ = new LinkedList<Integer>();
q = new LinkedList<Integer>();
}
public int max_value() {
if (maxQ.isEmpty()) {
return -1;
}
return maxQ.peekFirst();
}
public void push_back(int value) {
q.offer(value);
while ((!maxQ.isEmpty()) && maxQ.peekLast() < value) {
maxQ.pollLast();
}
maxQ.offer(value);
}
public int pop_front() {
if (q.isEmpty()) {
return -1;
}
int res = q.poll();
if (res == maxQ.peekFirst()) {
maxQ.poll();
}
return res;
}
}
224. 基本计算器
思路:实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式可以包含左括号 ( ,右括号 ),加号 + ,减号 -,非负整数和空格 。
输入: "(1+(4+5+2)-3)+(6+8)"
输出: 23
简单来说,这种带括号的基本上都会用到栈,这一题也是,关键在于我们栈中不仅要存储数值还有加减符号也要存,另外,遇到(时需要将之前算的结果入栈,而遇到)则将之前计算的结果出栈进行计算:
public int calculate(String s) {
Stack<Integer> stack = new Stack<Integer>();
// sign 代表正负
int sign = 1, res = 0;
int length = s.length();
for (int i = 0; i < length; i++) {
char ch = s.charAt(i);
if (Character.isDigit(ch)) {
int cur = ch - '0';
while (i + 1 < length && Character.isDigit(s.charAt(i + 1)))
cur = cur * 10 + s.charAt(++i) - '0';//读入的字符串数转化成数值
res = res + sign * cur;
} else if (ch == '+') {
sign = 1;
} else if (ch == '-') {
sign = -1;
} else if (ch == '(') {//遇到括号时,存入括号前的符号(正负号)以及括号之前算的res
stack.push(res);
res = 0;//存入后清0,也就是相当于接下来就是单独算括号内的数值之和
stack.push(sign);
sign = 1;
} else if (ch == ')') {//遇到反括号,取出括号之前的值,以及括号之前的符号,一并运算
res = stack.pop() * res + stack.pop();
}
}
return res;
}
227. 基本计算器 II
思路:实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式仅包含非负整数,+, - ,*,/ 四种运算符和空格 。 整数除法仅保留整数部分。
输入: " 3+5 / 2 "
输出: 5
这一题我想了一下不可以用上面那一题的模板,因为这里的*和/是有更高优先级的,所以不能遇到加减直接计算,而是需要看后面有没有*和/等,所以正确的方法应该是先把所有的*和/都先计算了,再把栈中的元素相加(遇到建好则存其相反数,栈中不存储符号):
public int calculate(String s) {
int res = 0, d = 0;//d表示每个数字及之前的符号的乘积,第一个数字之前的符号默认为+
char sign = '+';//初始默认符号
Stack<Integer> nums = new Stack<>();
for (int i = 0; i < s.length(); ++i) {
if (s.charAt(i) >= '0') {//加减乘除和空格ASCII码都小于'0'
d = d * 10 - '0' + s.charAt(i);//进位(先减法),每次只加一个字符而不是一个整数
}
if ((s.charAt(i) < '0' && s.charAt(i) != ' ') || i == s.length() - 1) {
if (sign == '+') {
nums.push(d);
} else if (sign == '-') {
nums.push(-d);
} else if (sign == '*' || sign == '/') {
int tmp = sign == '*' ? nums.pop() * d : nums.pop() / d;//这里觉得很奇怪,d好像并不是*或/后的数字(问题在于,sign并不是当前s.charAt(i),而是上一次s.charAt(i-1)的符号,这次的符号s.charAt(i)在最后才赋值)
//nums.pop();
nums.push(tmp);
}
sign = s.charAt(i); //保存当前符号(赋值当前符号)
d = 0;
}
}
for (; !nums.empty(); nums.pop()) {//将每个数字以及前面的符号的乘积入栈,最后加起来的时候一起出栈相加,与之前的方法不同,之前是括号内一步步算出来相加
res += nums.peek();
}
return res;
}