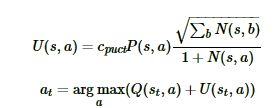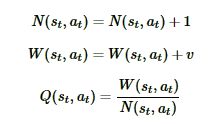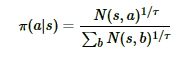用飞桨框架2.0造一个会下五子棋的AI模型——从小白到高手的训练之旅

点击左上方蓝字关注我们

【飞桨开发者说】洪伟，建筑行业BIM工程师、一级注册建造师，飞桨开发者，人工智能技术爱好者，相信“AI，正在让世界变得更美好”，感兴趣的方向有：强化学习（Reinforcement Learning）、图神经网络（Graph Neural Network）、图像处理。

还记得令职业棋手都闻风丧胆的“阿尔法狗”么？这里有“阿尔法狗”的小兄弟——AlphaZero-Gomoku-PaddlePaddle，即我用飞桨框架2.0从零开始训练自己的AI模型，在AI Studio上可随时随地开启五子棋小游戏。

五子棋游戏简介

五子棋是一种两人对弈的纯策略型棋类游戏，通常双方分别使用黑白两色的棋子，轮流下在棋盘竖线与横线的交叉点上，先形成五子连线者获胜。五子棋容易上手，老少皆宜，而且趣味横生，引人入胜。

项目简介

本项目是基于飞桨框架2.0对AlphaZero算法的一个实现，能够玩简单的棋盘游戏Gomoku（也称为五子棋），使用纯粹的自我博弈（Self-play）方式开始训练。

Gomoku游戏比围棋、象棋简单得多，因此我们可以专注于AlphaZero的训练。在一台PC机上，几个小时内就可以获得一个不可忽视的AI模型，因为一不留心，AI就可能战胜了你。

和围棋相比，五子棋的规则较为简单，落子空间也比较小，我没有用到AlphaGo Zero中大量使用的残差网络，只使用了卷积层和全连接层。也正是因为网络结构简单，只使用AI Studio的CPU环境也可以运行。不过，我还是建议使用GPU环境，程序会自动检测环境是否包含GPU，无需手动设置。本项目之前是用飞桨框架1.84版本写的，现在升级到飞桨框架2.0版本。

需要注意的是，AlphaZero是MuZero的“前辈”，了解AlphaZero有助于理解MuZero算法的来龙去脉。

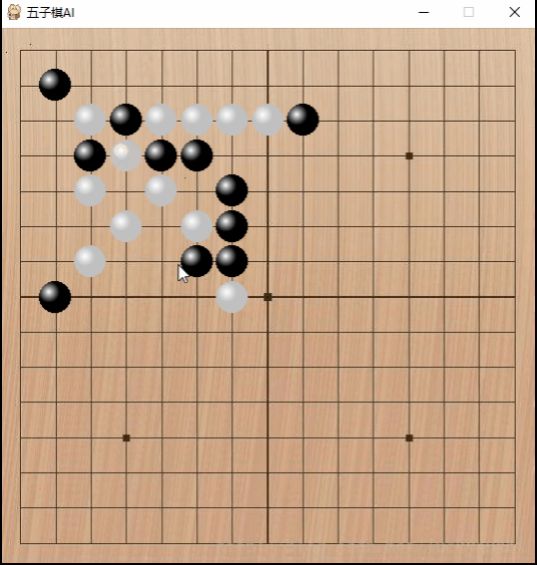
开始训练自己的AI模型时，请运行“python train.py”。开始人机对战或者AI互搏时，请运行“python human_play.py”。15x15棋盘左上角9x9范围下棋的效果展示：

让我们用飞桨框架2.0

打造一个会下五子棋的AI模型

首先，让我们开始定义策略价值网络的结构，网络比较简单，由公共网络层、行动策略网络层和状态价值网络层构成。

class Net(paddle.nn.Layer):
    def __init__(self,board_width, board_height):
        super(Net, self).__init__()
        self.board_width = board_width
        self.board_height = board_height
        # 公共网络层
        self.conv1 = nn.Conv2D(in_channels=4,out_channels=32,kernel_size=3,padding=1)
        self.conv2 = nn.Conv2D(in_channels=32,out_channels=64,kernel_size=3,padding=1)
        self.conv3 = nn.Conv2D(in_channels=64,out_channels=128,kernel_size=3,padding=1)
        # 行动策略网络层
        self.act_conv1 = nn.Conv2D(in_channels=128,out_channels=4,kernel_size=1,padding=0)
        self.act_fc1 = nn.Linear(4*self.board_width*self.board_height,
                                 self.board_width*self.board_height)
        self.val_conv1 = nn.Conv2D(in_channels=128,out_channels=2,kernel_size=1,padding=0)
        self.val_fc1 = nn.Linear(2*self.board_width*self.board_height, 64)
        self.val_fc2 = nn.Linear(64, 1)

    def forward(self, inputs):
        # 公共网络层 
        x = F.relu(self.conv1(inputs))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        # 行动策略网络层
        x_act = F.relu(self.act_conv1(x))
        x_act = paddle.reshape(
                x_act, [-1, 4 * self.board_height * self.board_width])

        x_act  = F.log_softmax(self.act_fc1(x_act))        
        # 状态价值网络层
        x_val  = F.relu(self.val_conv1(x))
        x_val = paddle.reshape(
                x_val, [-1, 2 * self.board_height * self.board_width])
        x_val = F.relu(self.val_fc1(x_val))
        x_val = F.tanh(self.val_fc2(x_val))

        return x_act,x_val

在定义好策略和价值网络的基础上，接下来实现PolicyValueNet类，该类主要定义：policy_value_fn()方法，主要用于蒙特卡洛树搜索时评估叶子节点对应局面评分、该局所有可行动作及对应概率，后面会详细介绍蒙特卡洛树搜索；另一个方法train_step()，主要用于更新自我对弈收集数据上策略价值网络的参数。

def policy_value_fn(self, board):
        """
        input: board
        output: a list of (action, probability) tuples for each available
        action and the score of the board state
        """
        legal_positions = board.availables
        current_state = np.ascontiguousarray(board.current_state().reshape(
                -1, 4, self.board_width, self.board_height)).astype("float32")

        current_state = paddle.to_tensor(current_state)
        log_act_probs, value = self.policy_value_net(current_state)
        act_probs = np.exp(log_act_probs.numpy().flatten())

        act_probs = zip(legal_positions, act_probs[legal_positions])

        return act_probs, value.numpy()
    def train_step(self, state_batch, mcts_probs, winner_batch, lr=0.002):
        """perform a training step"""
        # wrap in Variable
        state_batch = paddle.to_tensor(state_batch)
        mcts_probs = paddle.to_tensor(mcts_probs)
        winner_batch = paddle.to_tensor(winner_batch)

        # 参数的梯度归零
        self.optimizer.clear_gradients()
        # 设置学习率
        self.optimizer.set_lr(lr)


        # 前向运算
        log_act_probs, value = self.policy_value_net(state_batch)
        # 定义损失函数 = (z - v)^2 - pi^T * log(p) + c||theta||^2
        #注意: L2正则化项是在优化器创建的时候加入的
        value = paddle.reshape(x=value, shape=[-1])
        value_loss = F.mse_loss(input=value, label=winner_batch)
        policy_loss = -paddle.mean(paddle.sum(mcts_probs*log_act_probs, axis=1))
        loss = value_loss + policy_loss
        # 反向传播及优化
        loss.backward()
        self.optimizer.minimize(loss)
        # 计算交叉熵损失, 用于在训练过程中观察训练进度
        entropy = -paddle.mean(
                paddle.sum(paddle.exp(log_act_probs) * log_act_probs, axis=1)
                )
        return loss.numpy(), entropy.numpy()[0]    

在棋盘游戏中，玩家决定下一步怎么走的时候，往往会“多想几步”，AlphaZero也一样。我们用神经网络来选择最佳的下一步走法后，其余低概率的位置就被忽略了。

像Minimax这类传统的AI博弈树搜索算法，效率都很低。因为这些算法在做出最终选择前，需要穷尽每一种走法。即使是带有较少分支因子的游戏，也会使其博弈搜索空间变得像是脱缰的野马，让人难以驾驭。

分支因子就是游戏中所有可能走法的数量。这个数量会随着游戏的进行不断变化。因此，大家可以试着计算一个平均分支因子数，国际象棋的平均分支因子是35，而围棋则是250。这意味着，在国际象棋中，仅走两步就有1,225（35²）种可能的棋面，而在围棋中，这个数字会变成62,500（250²）。现在，神经网络将指导告诉我们哪些博弈路径值得探索，让大家避免被无用的搜索路径淹没。接着，蒙特卡洛树搜索算法即将登场啦！

蒙特卡洛树搜索

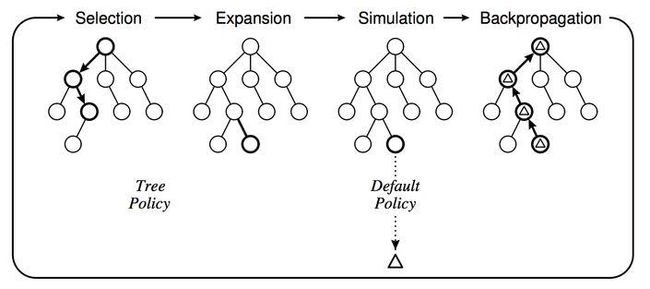
蒙特卡洛树搜索（Monte-Carlo Tree Search，以下简称MCTS），其具体做法如下：给定一个棋面，MCTS共进行N次模拟。主要的搜索阶段有4个——选择、扩展、仿真和回溯。

每个节点会记录4个值——N为记录节点的访问次数；u为节点的UCB值；Q为节点的价值；P为选择下一个动作的概率，策略p（s,a）。

第一步是选择（Selection）：这一步会从根节点开始，每次都选一个“最值得搜索的子节点”，一般使用UCT算法选择分数最高的节点，直到来到一个“存在未扩展子节点”的节点。

第二步是扩展（Expansion）：在这个搜索到且存在未扩展的子节点，加上一个没有历史记录的子节点，初始化子节点。

第三步是仿真（Simulation）：从上面这个没有试过的着法开始，用一个诸如快速走子策略（Rollout policy）的简单策略走到底，得到一个胜负结果。

第四步是回溯（Backpropagation）：将我们最后得到的胜负结果，回溯加到MCTS树结构上。大家要注意，除了之前的MCTS树要回溯外，新加入的节点也要加上一次胜负历史记录。

MCTS搜索完毕后，模型就可以在MCTS的根节点s基于以下公式选择行棋的MCTS分支了:

τ是用来控制探索的程度，τ的取值介于(0,1]之间。当τ越接近于1时，神经网络的采样越接近于MCTS的原始采样，当τ越接近于0时，神经网络的采样越接近于贪婪策略，即选择最大访问次数N所对应的动作。

因为在τ很小的情况下，直接计算访问次数N的τ次方根可能会导致数值异常。为了避免这种情况，在计算行动概率时，先将访问次数N加上一个非常小的数值（本项目是1e-10），取自然对数后乘上1/τ，再用一个简化的SoftMax函数将输出还原为概率，这和原始公式在数学上基本上是等效的。SoftMax()方法和get_move_probs()方法的代码分别如下：

def softmax(x):
            probs = np.exp(x - np.max(x))
            probs /= np.sum(probs)
return probs


    def get_move_probs(self, state, temp=1e-3):
        """按顺序运行所有播出并返回可用的操作及其相应的概率。
        state: 当前游戏的状态
        temp: 介于(0,1]之间的临时参数控制探索的概率
        """
        for n in range(self._n_playout):
            state_copy = copy.deepcopy(state)
            self._playout(state_copy)

        # 根据根节点处的访问计数来计算移动概率
        act_visits = [(act, node._n_visits)
                      for act, node in self._root._children.items()]
        acts, visits = zip(*act_visits)
        act_probs = softmax(1.0/temp * np.log(np.array(visits) + 1e-10))

        return acts, act_probs

关键点是什么？

• 通过每一次模拟，MCTS依靠神经网络，使用累计价值（Q）、神经网络给出的走法先验概率（P）以及访问对应节点频率的组合，沿着最有希望获胜的路径（也就是具有最高置信区间上界的路径）进行探索。

• 在每一次模拟中，MCTS会尽可能纵深地进行探索，直至遇到从未见过的盘面状态，在这种情况下，它会通过神经网络来评估该盘面状态的优劣。

具体代码可以自行查看项目文件。

训练算法介绍

AlphaZero的算法流程，概括来说就是通过自我对弈收集数据，并用于更新策略价值网络，更新后的策略价值网络又会被用于后续的自我对弈过程中，从而产生高质量的自我对弈数据，这样相互促进、不断迭代，实现稳定的学习和提升。

我们将训练流程定义为run()，会循环执行self.collect_selfplay_data()方法，从而收集自我对弈的数据，收集到的数据多于self.batch_size时，我们就调用self.policy_update()来更新策略价值网络。

def run(self):
        """开始训练"""
        root = os.getcwd()

        dst_path = os.path.join(root, 'dist')

        if not os.path.exists(dst_path):
            os.makedirs(dst_path)

        try:
            for i in range(self.game_batch_num):
                self.collect_selfplay_data(self.play_batch_size)
                print("batch i:{}, episode_len:{}".format(
                    i + 1, self.episode_len))
                if len(self.data_buffer) > self.batch_size:
                    loss, entropy = self.policy_update()
                    print("loss :{}, entropy:{}".format(loss, entropy))
                if (i + 1) % 50 == 0:
                    self.policy_value_net.save_model(os.path.join(dst_path, 'current_policy_step.model'))
                # 检查当前模型的性能，保存模型的参数
                if (i + 1) % self.check_freq == 0:
                    print("current self-play batch: {}".format(i + 1))
                    win_ratio = self.policy_evaluate()
                    self.policy_value_net.save_model(os.path.join(dst_path, 'current_policy.model'))
                    if win_ratio > self.best_win_ratio:
                        print("New best policy!!!!!!!!")
                        self.best_win_ratio = win_ratio
                        # 更新最好的策略
                        self.policy_value_net.save_model(os.path.join(dst_path, 'best_policy.model'))
                        if (self.best_win_ratio == 1.0 and
                                    self.pure_mcts_playout_num < 8000):
                            self.pure_mcts_playout_num += 1000
                            self.best_win_ratio = 0.0
        except KeyboardInterrupt:
            print('\n\rquit')

一些建议和技巧：

• 最好从6 * 6的棋盘、4子连成直线获胜开始训练。这样的话，我们可以在大约2个小时内，以500~1000局的自我博弈，获得一个不可忽视的模型。

• 对于 8 * 8 的棋盘、 5子连成直线获胜的情况, 大约需要2000~3000局的自我博弈，从而得到一个不可小视的模型。

• 在算力有限的情况下，如果想要尽快地收集对弈数据，可以将棋盘数据进行旋转和镜像翻转，并把得到的数据存入data buffer中。

最后再介绍下MuZero

MuZero是AlphaZero的后继者。与AlphaGo和AlphaZero相似，MuZero也使用MCTS汇总神经网络预测，并选择适合当前环境的动作。但MuZero不需要提供规则手册，只需通过自我试验，便能学会象棋围棋游戏和各种Atari游戏。除此以外，它还能通过考虑游戏环境的各个方面来评估局面是否有利以及策略是否有效，并可通过复盘游戏在自身错误中学习。

AlphaZero-五子棋-飞桨框架2.0版本：

https://aistudio.baidu.com/aistudio/projectdetail/1403398

极简MuZero算法实践-飞桨框架2.0版本：

https://aistudio.baidu.com/aistudio/projectdetail/1448859

相关论文：

1. AlphaZero: Mastering Chess and Shogi by Self-play with a General Reinforcement Learning Algorithm

2. AlphaGo Zero: Mastering the game of Go without human knowledge

可以参考的书籍：

• 郭宪，宋俊潇. 深入浅出强化学习编程实战 —— 电子工业出版社2020

• 邹伟. 强化学习 ——清华大学出版社 2020

如在使用过程中有问题，可加入官方QQ群进行交流：778260830。

如果您想详细了解更多飞桨的相关内容，请参阅以下文档。

·飞桨官网地址·

https://www.paddlepaddle.org.cn/

·飞桨开源框架项目地址·

GitHub: https://github.com/PaddlePaddle/Paddle 

Gitee: https://gitee.com/paddlepaddle/Paddle

????长按上方二维码立即star！????

飞桨(PaddlePaddle)以百度多年的深度学习技术研究和业务应用为基础，是中国首个开源开放、技术领先、功能完备的产业级深度学习平台，包括飞桨开源平台和飞桨企业版。飞桨开源平台包含核心框架、基础模型库、端到端开发套件与工具组件，持续开源核心能力，为产业、学术、科研创新提供基础底座。飞桨企业版基于飞桨开源平台，针对企业级需求增强了相应特性，包含零门槛AI开发平台EasyDL和全功能AI开发平台BML。EasyDL主要面向中小企业，提供零门槛、预置丰富网络和模型、便捷高效的开发平台；BML是为大型企业提供的功能全面、可灵活定制和被深度集成的开发平台。

END