基于遗传算法的南昌周边城市旅游规划研究（Python实现）

当前，国民生活水平得到大幅提升，人均汽车拥有量越来越多，自驾周边城市游也成为越来越多家庭节假日期间的选择，旅游路径规划成为研究热点。旅游路径规划问题是基于经典旅行商问题( TSP) 演变而来的，目前主要应用于物流路径规划领域。规模小的旅行商问题易计算解决，但规模较大情况下，传统计算方法无法解决，而遗传算法作为新兴智能优化算法，求解能力较强。通过建立旅行商模型，使用遗传算法寻求江西省南昌市周边共9个省会城市总距离最短的旅游路径，结果表明该方法有效且实用。
关键词: 旅行商问题；遗传算法；旅游路径规划
一、引言
（一）研究背景
随着科技的进步，人民生活品质的提升，用户对旅游的需求日益增加。尤其是旅游路线规划方面的需求，为用户设计满足个性化需求的旅行路线，提升游客的游玩体验变得越来越迫切。目前，随着互联网的普及，使得越来越多的游客对于从繁杂的旅游信息中找到满足自己需求的数据感到十分疲惫。其次，国内针对自助旅游路线规划系统或者网站的开发发展是缓慢的，无法贴合用户的实际需求。因此，整合旅游资源，挖掘出有价值的旅游信息，研究旅游路线规划问题是非常有意义的，具有潜在的开发空间和社会效益。
（二）研究意义
旅行商问题(Traveling Salesman Problem，TSP)称之为货担郎问题，TSP问题是一个经典组合优化的NP（Non-deterministic Polynomial）完全问题。组合优化问题是对存在组合排序或者搭配优化问题的一个概括，也是现实诸多领域相似问题的简化形式。在日常生活中，交通问题和物流运输安排无处不与日常生活相关的NP完全问题，除此之外，工业生产上的计算机网络通信工程、集成电路部署线路以及众多工业产品的加工排序调度都可以转化成TSP问题。因此，TSP问题依然具有很高的研究和应用价值，对于其求解的高效也至关重要。
（三）国内外研究现状
1.国外研究现状
国外旅游业发展较早，关于旅游路线规划的研究较早。1977年，Gunn对旅游规划中的TSP问题进行研究，利用启发式算法解决TSP规划过程中过早收敛和低速问题。2009年Schilde等人通过多目标定向算法，解决城市旅游中多目标旅游路线规划问题。针对每个游客有不同的旅游偏好，应用帕累托蚁群优化算法设计出使游客满意的个性化旅游路线。2011 年，Alhanjouri利用遗传算法和蚁群算法解决初始化参数设置对旅行商最佳路线的影响。2016年，Amith AL通过启发式的最短路径算法解决复杂旅游路线优化问题，并且路线规划效果良好。2017 年，Cenamor等人推出了Plan Tour，这是一种旅游社交推荐系统，它可以根据收集到的社交网络热门旅游信息，利用聚类算法，根据旅行时间，为用户推荐旅游路线。但是这种推荐的旅游路线是固定的，一般推荐的游玩路线，旅游周期较长。2018年Hasuike等人利用改进的动态Dijkstra算法，建立数学模型，求解基于时间限制的旅游路线规划问题。
2.国内研究现状
近些年来，国内关于旅游线路规划深层次的研究也是很多的。邹时林等人以庐山景区为例，结合景区知名度以及景区停留时间，利用最短路径算法，通过改进GIS中的最短路径，为游客推荐庐山一日游路线。曹旭利用改良圈算法建立 TSP问题的旅游线路优化设计模型。李迎利用推荐算法求解多目标路径规划问题，最后得到基于地理位置的路径推荐，经测试该推荐方法在推荐的精确率方面效果较优。王晓婷利用改进蚁群算法提高全局最优解的质量，将景区中道路因子、等待因子、兴趣因子为影响因子建立数学模型，以游客满意度作为评价标准，分析了蚁群算法在路径规划中的应用，结果证明改进后的蚁群算法求解基于游客满意度的路线图，较之前游客满意度效果确实显著。目前，一种广泛的求解旅游路线规划问题的方法是利用遗传算法或者基于遗传算法和其他智能优化算法的混合算法。陆青结合多智能体技术和交互式遗传算法，通过改进遗传算法，用来缓解用户在旅游评价过程中的疲劳问题。黄腾基于TSP模型的研究，利用遗传算法和蚁群算法分别对方案进行优化，有效规划湖南省景区旅游路线。
近十年来，学者们针对遗传算法求解TSP问题的改进主要集中在种群初始化、操作算子和算法融合方面。宋丹在遗传算法的基础上，针对TSP问题，提出顶端培育和分阶段策略，用来加强种群多样性。陶丽华等人通过将遗传算法和蚁群算法动态融合，并在遗传算法中改进重插入子代操作，应用于TSP问题，有较好的寻优能力、算法稳定性。吴兴健在算法初期，通过添加Delaunay三角剖分的策略缩小所求问题的搜索范围，引入云关联规则，帮助交叉变异操作可以实现自适应调节，实验显示改进后的算法性能较强，结果更优。
3.小结
文章基于目前研究状况，以江西省南昌市为中心，距离最短为目标函数，通过经度、纬度来研究其周边共9个省会城市或直辖市(上海、南京、合肥、武汉、长沙、南昌、广州、泉州、杭州) 出行旅游最短路径，并且利用遗传算法对其进行求解，结果证明遗传算法在解决周边游路径规划问题方面具有较高的实用性。
二、旅行商（TSP）问题的概述
（一）TSP问题的定义
19 世纪初，旅行商问题（TSP）被提出，随后经过众多学者研究的深入研究，被广泛应用于各个领域。旅行商问题的基本思想是：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路，TSP问题的目标就是最终求解出所旅行的所有可能行程中最短行程。它是组合优化中的一个多项式复杂程度的非确定性问题（NP完全问题），在运筹学和理论计算机科学中非常重要。
（二）TSP问题的描述
旅行商问题利用图论中的知识可以描述为在一个正权图 G=(V,E ,r)中，遍历G中每一个节点并且形成简单的回路，使各边权重相加之和最小，其中顶点集合为 V={1,2,…,n}，表示被访问的城市；边集合E是连接V中两个不同点之间的边集；r表示两个城市之间的权重即距离。旅行商问题就是在一个由顶点V和边集E组成的一个闭合无交叉连同无向图的Hamiltion回路，且需要该无向图的权值最小。面对点集合的数据猛增，对于这样一个满足Hamiltion回路的可能组合也会成指数级增长。由此，旅行商问题也属于NP-Hard完全问题，因而能够很快精确求出近似最优解也变得意义重大。其数学模型定义如下：


（三）TSP问题的处理算法
1.穷举法
TSP的描述虽然简单，解决起来却很困难，最简单思路是用穷举法把所有可能的巡回路径全部列出来，最短的一个就是最优解，这种方法就是枚举法，又称穷举法，它的解是多维的、多局部极值的、趋于无穷大的复杂解的空间，搜索空间是n个点的所有排列的集合。但这种处理方法只能处理很小规模的问题，不能在多项式时间内求解。如果有n座城市，那么巡游路径共有 条，计算的时间和成正比。
2.分支限界法
分枝限界法是由达金和多伊格在上世纪60年代初提出的。 为了避免盲目搜索，人们提出了改进的分枝限界方法—LC分枝限界法，它是一种应用范围很广的搜索算法，其通过有效约束界限来控制搜索进程，使之能向着状态空间树上有最优解的分支推进，以便尽快找出一个最优解，该方法的基本思想是：根据智能化的判定函数，只产生解的部分状态空间树，从而加速搜索过程， 即通过计算一小部分可行解即可以找到最优解。
3.模拟退火算法
1982年Patrick K 将退火思想引入组合优化领域提出一种求解大规模组合优化问题的算法。模拟退火算法（Simulated Annealing‚简称SA）的核心是模拟物理中固体物质的退火过程‚它的基本思想是：用热力学系统来模拟求解的优化问题‚把系统的能量看成是优化问题的目标函数‚用系统逐步降温以达到最低能量状态的退火过程去模拟优化过程。它从一定初始解开始‚从邻域中随机产生另一个解接受准则允许目标函数在有限范围内变坏。
4.遗传算法
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，按照适者生存和优胜劣汰原理，逐代演化产生出越来越好的近似解。在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。 这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。
三、遗传算法模型构建
（一）概念定义
遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。

（三）实现过程
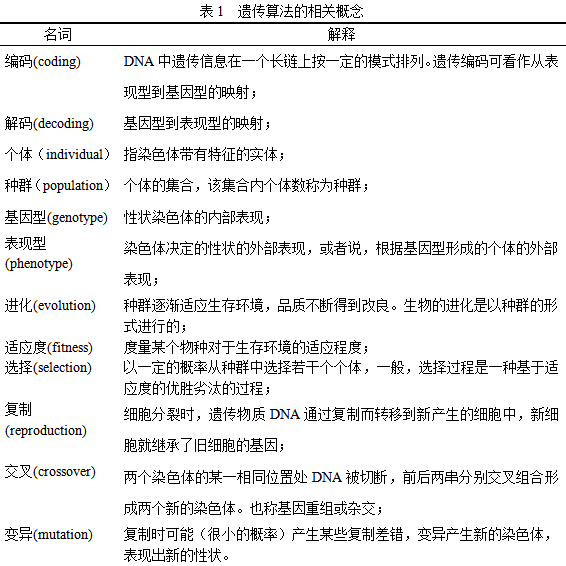
遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。
染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码。
初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。
（四）一般步骤
1.编码
随机产生一个初始种群，寻找一种合适的编码方案对种群中的个体进行编码，初始化各个运行参数，并对初始种群里的个体进行编码；
2.选择
根据适应度函数对种群中的每个个体进行适度值计算，保留适应度值较大的个体，以此不断淘汰适应度低的个体；
3.复制、交叉和变异
将保留下的个体分别进行复制、交叉和变异等算子进行操作，产生出子代；
4.循环迭代
所有种群个体均执行完所有操作，再根据迭代次数或解的阈值决定是否继续执行算法，最终输出最优个体。

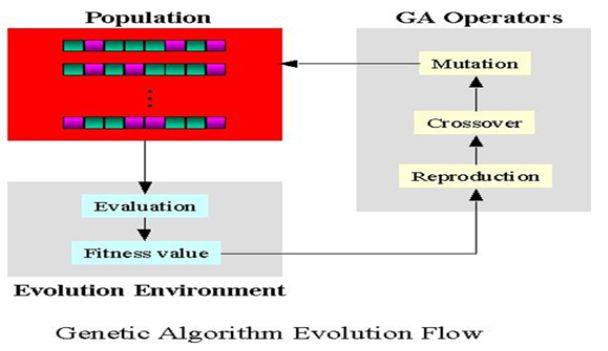
图1 遗传算法的一般步骤




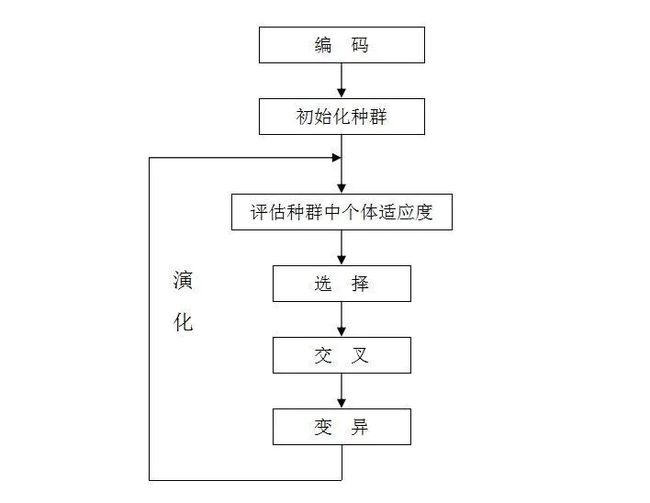
图2 遗传算法流程图
四、实验结果及分析
根据上面所构建的模型和具体的遗传算法步骤，文章基于 Python 语言对遗传算法进行代码实现，利用遗传算法对模型求解。首先获取9个省会城市或直辖市(上海、南京、合肥、武汉、长沙、南昌、广州、泉州、杭州) 的地理位置坐标，分布如图3所示。

图3 南昌及周边省会城市分布散点图
通过对地理位置的转化求解9个城市先后游玩的最短距离。在设定的参数以及算法收敛原则情况下得到最优结果为30.562636997125463，具体路径为南昌—合肥—南京—上海—杭州—福州—广州—长沙—武汉—南昌，具体路线图如下图4所示。图5给出了该算法的收敛曲线图，也可直观地看出该算法具有较强的收敛性能。

图4 最短路径图

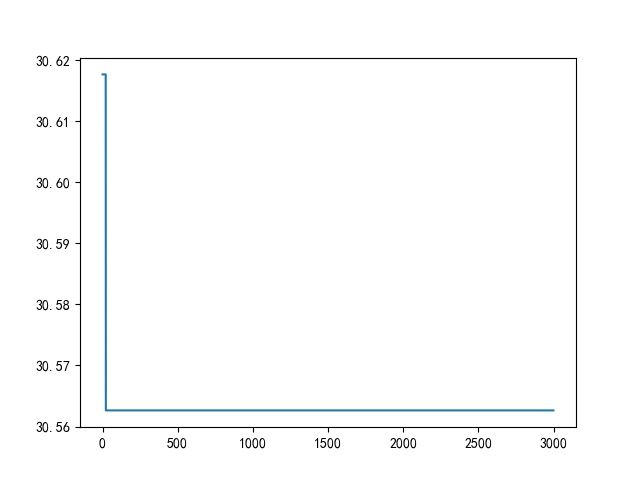
图5 路径收敛曲线
综上所述，南昌周边9个省会城市旅游最短路径得以解决，可见遗传算法对于解决南昌城市周边游路径规划问题效果显著，对上述九个城市居民采取周边游都具有很好的建议；但是论文仍有不足，第一，各城市数据采取的地理经纬度导致最终距离很小，这与真实地图数据有点差距，但是整体结果符合真实地图；第二，本实验中是将遗传算法中各参数固定，但是对于不同的参数可能会出现不同情况，综上这些不足在未来实验中可以继续改进。
参考文献
[1]葛海明. 改进的遗传算法求解TSP问题的应用与研究[D].江西理工大学,2016.
[2]于莹莹,陈燕,李桃迎.改进的遗传算法求解旅行商问题[J].控制与决策,2014,29(08):1483-1488.DOI:10.13195/j.kzyjc.2013.0598.
[3]孙娴.关于旅行商问题的数学模型[J].科学技术创新,2019(17):19-20.
[4]徐伟华,魏传祥,张根瑞,赵彩梅,熊坚.基于K-近邻域搜索的遗传算法求解旅行商问题[J].昆明理工大学学报(自然科学版),2022,47(01):139-146.DOI:10.16112/j.cnki.53-1223/n.2022.01.481.
[5]吴军,严丽娜.基于改进的遗传算法求解旅行商问题[J].中小企业管理与科技(下旬刊),2017(03):96-98.
[6]闫茹. 基于改进遗传算法的旅游路线优化研究与应用[D].北方民族大学,2021.DOI:10.27754/d.cnki.gbfmz.2021.000094.
[7]李振业,陈婷,陈静.基于遗传算法的旅游最优路径探究[J].电脑知识与技术,2018,14(34):181-183+188.DOI:10.14004/j.cnki.ckt.2018.4038.
[8]高珩,鲍鹏.旅行商问题求解算法综述[J].软件导刊,2009,8(11):67-68.
[9]王剑文,戴光明,谢柏桥,张全元.求解TSP问题算法综述[J].计算机工程与科学,2008(02):72-74+155.
[10]张立毅,高杨,费腾,王玉婧.求解旅行商问题的搜寻者遗传算法[J].数学的实践与认识,2019,49(07):115-122.
[11]程荣.遗传算法求解旅行商问题[J].科技风,2017(16):40+51.DOI:10.19392/j.cnki.1671-7341.201716037.
[12]尹艺珂. 城市物流配送路径优化算法研究与应用[D].西安石油大学,2021.DOI:10.27400/d.cnki.gxasc.2021.000607.
[13]王雪兵. 基于遗传算法的Y物流公司配送路径优化研究[D].中北大学,2021.DOI:10.27470/d.cnki.ghbgc.2021.000075.
[14]孙树栋, 遗传算法原理与应用. 陕西省,西北工业大学,2005-05-12.
[15]李少波,宋启松,李志昂,张星星,柘龙炫.遗传算法在机器人路径规划中的研究综述[J].科学技术与工程,2020,20(02):423-431.
附录
（一）Python代码
基于Python的遗传算法解决TSP问题

import numpy as np
import matplotlib.pyplot as plt
import math
import random

# 种群数
population_num = 300
# 改良次数
improve_count = 1000
# 进化次数
iter_count = 3000
# 设置强者的概率，种群前30%是强者，保留每代的强者
retain_rate = 0.3
# 设置弱者的存活概率
live_rate = 0.5
# 变异率
mutation_rate = 0.1
# 起始点
origin = 5

'''
载入数据
'''
def read_data():
    city_name = []
    city_position = []
    with open("demo_9.txt", 'r') as f:
        lines = f.readlines()
        for line in lines:
            line = line.split('\n')[0]
            line = line.split('\t')
            city_name.append(line[0])
            city_position.append([float(line[1]), float(line[2])])
    city_position = np.array(city_position)

    plt.scatter(city_position[:, 0], city_position[:, 1])
    plt.savefig("城市散点图.jpg")
    plt.show()

    return city_name, city_position

'''
计算距离矩阵
'''
def distance_Matrix(city_name, city_position):
    global city_count, distance_city
    city_count = len(city_name)
    distance_city = np.zeros([city_count, city_count])
    for i in range(city_count):
        for j in range(city_count):
            distance_city[i][j] = math.sqrt((city_position[i][0] - city_position[j][0]) ** 2 + (city_position[i][1] - city_position[j][1]) ** 2)
    return city_count, distance_city

'''
获取一条路径的总距离
'''
def get_distance(path):
    distance = 0
    distance += distance_city[origin][path[0]]
    for i in range(len(path)):
        if i == len(path) - 1:
            distance += distance_city[origin][path[i]]
        else:
            distance += distance_city[path[i]][path[i + 1]]
    return distance

'''
改良
'''
def improve(path):
    distance = get_distance(path)
    for i in range(improve_count):    # 改良迭代
        u = random.randint(0, len(path) - 1)  # 在[0, len(path)-1]中随机选择交换点下标
        v = random.randint(0, len(path) - 1)
        if u != v:
            new_path = path.copy()
            t = new_path[u]
            new_path[u] = new_path[v]
            new_path[v] = t
            new_distance = get_distance(new_path)
            if new_distance < distance:  # 保留更优解
                distance = new_distance
                path = new_path.copy()

'''
杰出选择
先对适应度从大到小进行排序，选出存活的染色体，再进行随机选择，选出适应度小但是存活的个体
'''
def selection(population):
    # 对总距离进行从小到大排序
    graded = [[get_distance(path), path] for path in population]
    graded = [path[1] for path in sorted(graded)]
    # 选出适应性强的染色体
    retain_length = int(len(graded) * retain_rate)
    parents = graded[: retain_length]   # 保留适应性强的染色体
    for weak in graded[retain_length:]:
        if random.random() < live_rate:
            parents.append(weak)
    return parents

'''
交叉繁殖
'''
def crossover(parents):
    # 生成子代的个数，以此保证种群稳定
    children_count = population_num - len(parents)
    # 孩子列表
    children = []
    while len(children) < children_count:
        male_index = random.randint(0, len(parents) - 1)  # 在父母种群中随机选择父母
        female_index = random.randint(0, len(parents) - 1)
        if male_index != female_index:
            male = parents[male_index]
            female = parents[female_index]
            left = random.randint(0, len(male) - 2)   # 给定父母染色体左右两个位置坐标
            right = random.randint(left + 1, len(male) - 1)
            # 交叉片段
            gen1 = male[left : right]
            gen2 = female[left : right]
            # 通过部分匹配交叉法获得孩子
            # 将male和female中的交叉片段移到末尾
            male = male[right:] + male[:right]
            female = female[right:] + female[:right]
            child1 = male.copy()
            child2 = female.copy()

            for o in gen2:   # 移除male中存在于gen2交换片段上的基因
                male.remove(o)
            for o in gen1:   # 移除female中存在于gen1交换片段上的基因
                female.remove(o)

            # 直接替换child上对应的基因片段
            child1[left:right] = gen2
            child2[left:right] = gen1

            # 调整交换片段两侧的基因
            child1[right:] = male[0: len(child1) - right]  # 将原male交叉片段右侧长度对应的现male片段给child
            child1[:left] = male[len(child1) - right: ] # 将现male靠后的片段是原male的左侧片段

            child2[right:] = female[0: len(child2) - right]
            child2[:left] = female[len(child2) - right:]

            children.append(child1)
            children.append(child2)
    return children

'''
变异: 随机选取两个下标交换对应的城市
'''
def mutation(children):
    for i in range(len(children)):
        if random.random() < mutation_rate:  # 变异
            child = children[i]
            u = random.randint(0, len(child) - 2)
            v = random.randint(u + 1, len(child) - 1)
            tmp = child[u]
            child[u] = child[v]
            child[v] = tmp

'''
返回种群的最优解
'''
def get_result(population):
    graded = [[get_distance(path), path] for path in population]
    graded = sorted(graded)
    return graded[0][0], graded[0][1]  # 返回种群的最优解

'''
遗传算法
'''
def GA_TSP():
    city_name, city_position = read_data()
    city_count, distance_city = distance_Matrix(city_name, city_position)
    list = [i for i in range(city_count)]
    list.remove(origin)
    population = []
    for i in range(population_num):
        # 随机生成个体
        path = list.copy()
        random.shuffle(path)
        improve(path)
        population.append(path)
    every_gen_best = []  # 存储每一代最好的
    distance, result_path = get_result(population)
    for i in range(iter_count):
        # 选择繁殖个体群
        parents = selection(population)
        # 交叉繁殖
        children = crossover(parents)
        # 变异
        mutation(children)
        # 更新种群，采用杰出选择
        population = parents + children

        distance, result_path = get_result(population)
        every_gen_best.append(distance)

    print("最佳路径长度为：", distance)
    result_path = [origin] + result_path + [origin]
    print("最佳路线为：")
    for i, index in enumerate(result_path):
        print(city_name[index] + "(" + str(index) + ")", end=' ')
        if i % 9 == 0:
            print()

    X = []
    Y = []
    for i in result_path:
        X.append(city_position[i, 0])
        Y.append(city_position[i, 1])

    plt.figure()
    plt.rcParams['font.sans-serif'] =                                                                                                                                                                                                                                                                                                                                                                                         ['SimHei']  # 用来正常显示中文标签
    # plt.subplot(2,1,1)
    plt.plot(X, Y, '-o')
    plt.xlabel('经度')
    plt.ylabel('纬度')
    plt.title("GA_TSP")
    for i in range(len(X)):
        plt.annotate(city_name[result_path[i]], xy=(X[i], Y[i]), xytext=(X[i] + 0.1, Y[i] + 0.1))  # xy是需要标记的坐标，xytext是对应的标签坐标

    # plt.subplot(2,1,2)
    # plt.plot(range(len(every_gen_best)), every_gen_best)
    plt.savefig("路径规划图.jpg")
    plt.show()


if __name__ == '__main__':
    GA_TSP()

（二）南昌及周边省会城市经纬度