TensorFlow笔记之单变量线性回归

---

前言

记录使用TensorFlow1.x和TensorFlow2.x完成单变量线性回归的过程。

---

一、数据集生成

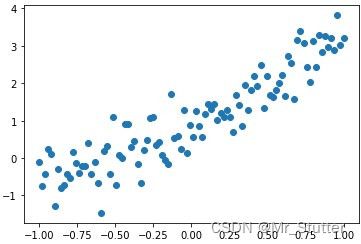
生成带标准正态分布噪声的y=2x+1数据集

import numpy as np
import matplotlib.pyplot as plt
#数据集生成
x_data = np.linspace(-1, 1, 100)
#引入随机数噪声
np.random.seed(0)
y_data = 2 * x_data + 1 + 0.5 * np.random.randn(x_data.shape[0])
plt.scatter(x_data, y_data)

二、TensorFlow1.x

1.定义模型

import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
#创建变量
x = tf.placeholder('float', name='x')
y = tf.placeholder('float', name='y')
w = tf.Variable(0.0, name='w')
b = tf.Variable(0.0, name='b')
#构建模型
def model(x, w, b):
    return w * x + b
#预测节点
pred = model(x, w, b)

2.训练模型

#训练参数:训练轮数,学习率
train_epoch = 10
learning_rate = 0.01
#显示损失函数
step = 0
display_step = 5
loss_list = []
loss_function = tf.reduce_mean(tf.square(y - pred))
#定义优化器,给定学习率,以最小化损失函数为目的
optimizer = tf.train.GradientDescentOptimizer(learning_rate)\
    .minimize(loss_function)
#变量初始化
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
#迭代训练
for epoch in range(train_epoch):
    for xi, yi in zip(x_data, y_data):#按第一维度拼接
        #权重更新
        _, loss = sess.run([optimizer, loss_function], feed_dict={x:xi, y:yi})
        #显示训练过程
        step = step + 1
        if step%display_step == 0:
            loss_list.append(loss)
    print('w=',sess.run(w),'b=',sess.run(b))
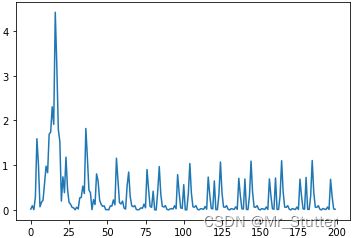
plt.plot(loss_list)

权重更新趋于稳定

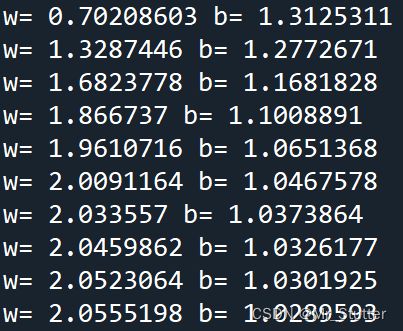
随机梯度下降，每次使用一个样本进行训练，损失函数整体上逐渐减小，受单个数据点的影响产生波动

3.模型预测

x_test = np.linspace(1, 10, 100)
y_test = 2 * x_test + 1
y_pred = sess.run(pred, feed_dict={x:x_test})
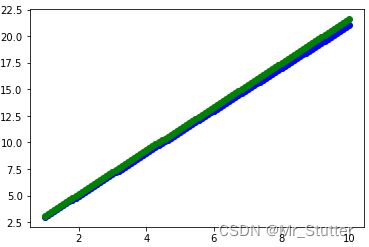
plt.scatter(x_test, y_test, c='b')
plt.scatter(x_test, y_pred, c='g')
sess.close()

三、TensorFlow2.x

1.定义模型

import tensorflow as tf
#创建变量
w = tf.Variable(np.random.randn(), tf.float32)
b = tf.Variable(np.random.randn(), tf.float32)
#建立模型
def model(x, w, b):
    return w * x + b

2.训练模型

#定义超参数
train_epoch = 50
learning_rate = 0.1
#显示损失函数
step = 0
display_step = 1
loss_list = []
def loss_function(x, y, w, b):
    pred = w * x + b
    loss = tf.reduce_mean(tf.square(y - pred))
    return loss
#迭代训练
for epoch in range(train_epoch):
    #自动求导
    with tf.GradientTape() as tape:
        loss = loss_function(x_data, y_data, w, b)
        grad_w, grad_b = tape.gradient(loss, [w, b])
    #显示训练过程
    step = step + 1
    if step % display_step == 0:
        print('w=', w.numpy(), 'b=', b.numpy())
        loss_list.append(loss.numpy())
    #权重更新
    w.assign_sub(grad_w * learning_rate)
    b.assign_sub(grad_b * learning_rate)
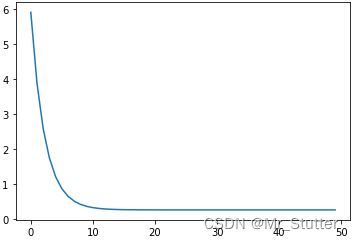
plt.plot(loss_list)

批量梯度下降，每次使用整个数据集进行训练，受单个数据点的影响较小，由于权重更新频率降低，需要适当增加学习率与训练轮数

3.模型预测

x_test = np.linspace(1, 10, 100)
y_test = 2 * x_test + 1
y_pred = w * x_test + b
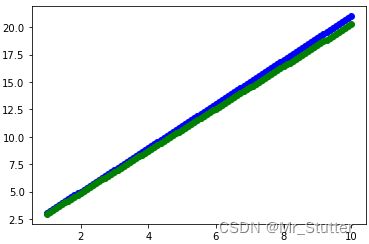
plt.scatter(x_test, y_test, c='b')
plt.scatter(x_test, y_pred, c='g')

---

总结

TensorFlow1.x使用梯度下降优化器进行权重更新，而TensorFlow2.x使用求导工具进行权重更新。1.x向2.x切换时需要退出控制台以重启命令式编程。随机梯度下降每次使用一个样本进行权重更新，计算量小，受单个数据点的影响较大；批量梯度下降每次使用所有样本进行权重更新，受单个数据点的影响较小，需要迭代的次数增加，计算量大；随机梯度下降每次使用部分样本进行权重更新，介于两者之间，当样本量和样本间差异较大可以选用。