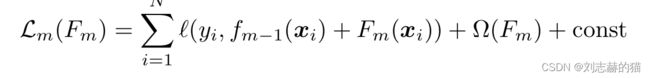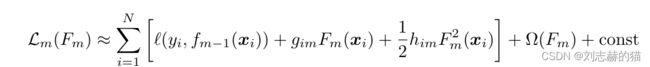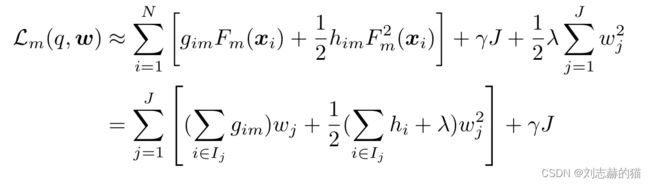CART、ensemble、XGB
这篇笔记记录一些树模型的基本概念和高阶话题,内容包括:
内容
- 1. CART
-
- 1.1 创建树
- 1.2 修剪树
- 2. 集成方法
-
- 2.1stacking
- 2.2bagging
- 2.3 RF
- 2.4boosting
- 3.实现
1. CART
1.1 创建树
树模型是一类常用分类、回归模型。通过将特征空间划分为 R 1 , . . . , R J R_1,...,R_J R1,...,RJ,每一类特征空间 R j R_j Rj设置对应的权重 w j w_j wj,利用加权平均对未知数据进行预测,

举一个例子。
假设有数据集 D \mathcal{D} D,通过一些特征信息(年龄、有无工作等),决定是否为其办理业务,label是真实标签:
| ID | 年龄 | 有工作 | 有房子 | 收入 | label |
|---|---|---|---|---|---|
| 1 | 32 | 有 | 无 | 1000 | 否 |
| 2 | 35 | 有 | 有 | 4000 | 是 |
| 3 | 66 | 无 | 有 | 3000 | 是 |
| 4 | 38 | 有 | 无 | 1000 | 否 |
| 5 | 22 | 有 | 有 | 4000 | 是 |
| 6 | 45 | 无 | 有 | 3000 | 是 |
| 7 | 27 | 有 | 无 | 1000 | 否 |
| 8 | 35 | 有 | 有 | 4000 | 是 |
| 9 | 46 | 无 | 有 | 3000 | 是 |
用树模型进行分类的流程如下:
于是需要确定问题是:
①每次依据哪个特征进行划分(特征选择, j ∗ j^* j∗)
②每次划分以哪个特征值为准(特征值选择, t ∗ t^* t∗)
首先,选择的特征要使划分后数据集有明显区分,比如有无房子的特征,每个样本的取值都是有,那么选择有无房子作为特征去划分样本集就没什么意义,因为所有的数据都会被划分到同一类。所以,选择的特征应该使得数据集的不确定性降低。
为了求解模型参数,转化为优化问题:

上述离散不可微的目标函数 L \mathcal{L} L,找到最优树是NP难的问题,因此常采用贪婪算法,每一步保证最优:
一般在每次划分节点时,尝试用每个特征、每个数据集该特征的值作为特征值,遍历找到解:
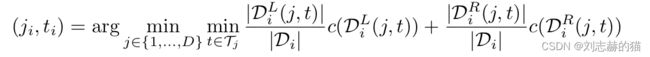
特征值连续时: D i L ( j , t ) = { ( x ( n ) , y n ) ∈ N i : x ( n ) < t } \mathcal{D}_i^L(j,t)=\{(x^{(n)},y_n)\in N_i:x^{(n)}
特征值离散时: D i L ( j , t ) = { ( x ( n ) , y n ) ∈ N i : x ( n ) = t } \mathcal{D}_i^L(j,t)=\{(x^{(n)},y_n)\in N_i:x^{(n)}=t\} DiL(j,t)={(x(n),yn)∈Ni:x(n)=t}
常用的损失函数 c c c有均方、信息熵、基尼指数等等。
1.2 修剪树
树模型的一个缺点是,当所有特征划分完成形成树后,整个模型有可能过拟合。这时主要采用剪枝的策略,将冗余的部分剪掉。
2. 集成方法
树模型的另一个缺点是不稳定,当数据集发生微小变动,预测结果会变化,对此,常采用集成方法,多次预测取平均或者多次预测取多数人的结果。

为什么这样的多人投票是有效的?假设一个模型的准确率是 θ \theta θ, Y m ∈ { 0 , 1 } Y_m\in\{0,1\} Ym∈{0,1}是第m个模型, S = ∑ m = 1 M Y m S=\sum_{m=1}^M Y_m S=∑m=1MYm是模型预测1的次数,如果是多人表决的原则,那么最终预测结果为1的概率
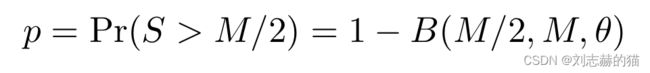
B是二项分布。
2.1stacking
2.2bagging
若用放回抽样形成M个样本集训练M个学习器,这样的思想叫bagging。
2.3 RF
若在每次特征划分时都只用随机的一部分数据,这样的思想叫随机森林。
2.4boosting
boosting是针对加法模型的求解方法,加法模型:

优化问题即最小化损失函数:

设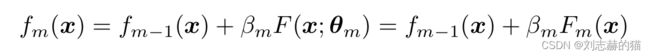
则
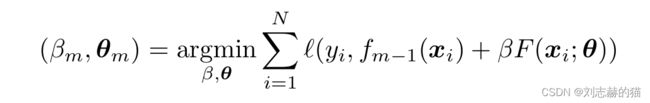
示例:
least square boosting
l ( y , , y ^ ) = ( y − y ^ ) 2 l(y,,\hat{y})=(y-\hat y)^2 l(y,,y^)=(y−y^)2
gradient boosting
以上是根据损失函数的角度区分不同的boosting方法,而更一般的视角是用函数空间, f m = f m − 1 − β m g m f_m=f_{m-1}-\beta_m g_m fm=fm−1−βmgm