机器学习实战——关联分析

1 关联分析介绍

关联分析又称关联挖掘，就是在交易数据、关系数据或其他信息载体中，查找存在于项目集合或对象集合之间的频繁模式、关联、相关性或因果结构。下面介绍关联分析中几个常用的概念：
项集：商品构成的集合，集合含有几个商品就称为几项集，如 {啤酒、尿布} 为二项集。
关联规则：商品间具有 $X\to Y$ 的形式，左侧的 $X$ 为先决条件，右侧的 $Y$ 为相应的关联结果。
频繁项集：某一项集的支持度大于规定的支持度阈值。
支持度：在所有项集中 $\{X,Y\}$ 出现的可能性，即项集中同时出现 $X,Y$ 的概率，其形式为：

$$Support(X\to Y)=P(X,Y)$$

置信度：关联规则的先决条件 $X$ 发生的条件下，$Y$ 发生的概率，其形式为：

$$Confidence(X\to Y)=P(Y|X)=\frac{P(X,Y)}{P(X)}$$

提升度：含有 $X$ 的条件下同时含有 $Y$ 的概率与所有项集中含有 $Y$ 的概率之比，其形式为：

$$Lift(X\to Y)=\frac{P(Y|X)}{P(Y)}=\frac{Confidence(X\to Y)}{P(Y)}$$

当提升度等于 1 时，X 与 Y 是相互独立的，即 X 的出现对 Y 无提升作用，表明 $X\to Y$ 是无效的强关联规则；大于 1（值越大） 时，即 X 的出现对 Y 有较大的提升作用，表明 X\rightarrow Y 是有效的强关联规则。在强关联规则的发现中，需要设定最小的支持度、置信度，而提升度是置信度的互补指标。
目前，比较常用的关联分析方法主要有 Apriori 算法、FP-Tree 算法。

1.1 Apriori 算法

Apriori 算法的基本思想是：利用最小支持度，从 1 项集开始不断的查找频繁项集直到找到最大的 k 项频繁项集，例如：找到符合支持度的频繁项集为 $A,B$ 与 $A,B,C$ ，则最终查找的频繁项集为 $A,B,C$ 。在 Apriori 算法中，若某个项集是频繁的，那么它的所有子集（同数学集合中的概念）也是频繁的；若项集是非频繁的，则其所有超集（所有包括该项集的集合）也是非频繁的。其查找频繁项集的流程如下：
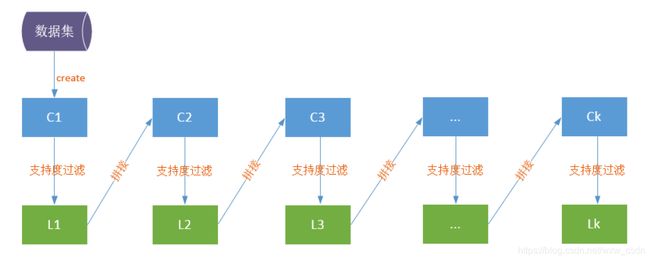以下表中的商品列表中 9 条商品为例对上述流程进行说明。

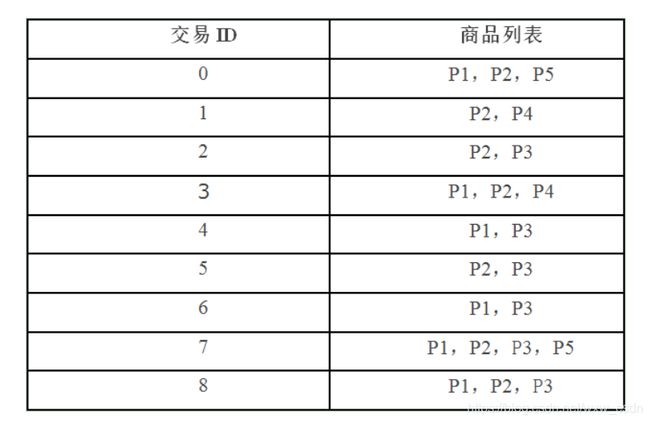
Apriori 算法发现频繁项集的具体流程如下：

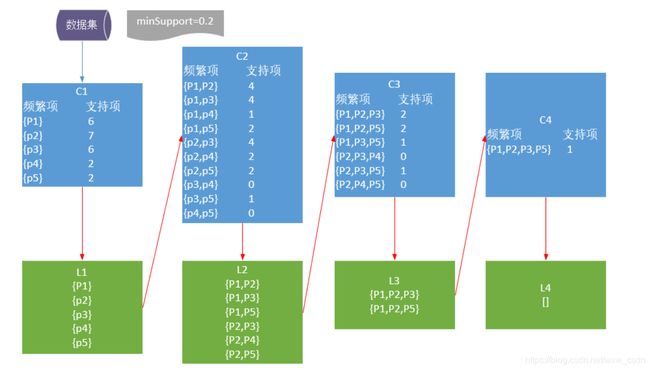
则 Apriori 算法的数学流程可以表述成如下的形式：
输入：数据集合 D，支持度阈值 $\alpha$
输出：最大的频繁 k 项集
1）扫描整个数据集，得到所有出现过的数据，作为候选频繁 1 项集。k=1，频繁 0 项集为空集。
2）挖掘频繁 k 项集：扫描数据计算候选频繁 k 项集的支持度；去除候选频繁 k 项集中支持度低于阈值的数据集,得到频繁 k 项集，若得到的频繁 k 项集为空，则直接返回频繁 k-1 项集的集合作为算法结果，算法结束，若得到的频繁 k 项集只有一项，则直接返回频繁 k 项集的集合作为算法结果，算法结束。基于频繁 k 项集，连接生成候选频繁 k+1 项集。
3） 令 k=k+1，转入步骤 2。
从算法的步骤可以看出，Apriori 算法每轮迭代都要扫描数据集，因此在数据集很大，数据种类很多的时候，算法效率很低。

1.2 FP-Growth 算法

FP-Growth 算法（也称 FP-Tree 算法），只需要扫描两次数据集，大大提高了算法运行的效率。

FP-Growth 算法工作流程如下：

1 构建 FP 树：第一遍扫描数据，对所有元素 1 项集出现的次数进行计数(如果某元素不频繁，那么该元素的超集也不频繁)，记录所有的 1 项频繁集出现的次数，并按照次数降序排列。
2 第二遍扫描，利用 FP 树挖掘频繁项集。
下面以刘建平博客中的例子对 FP-Growth 算法进行介绍

该例子中共有 10 条数据，其情况如下：
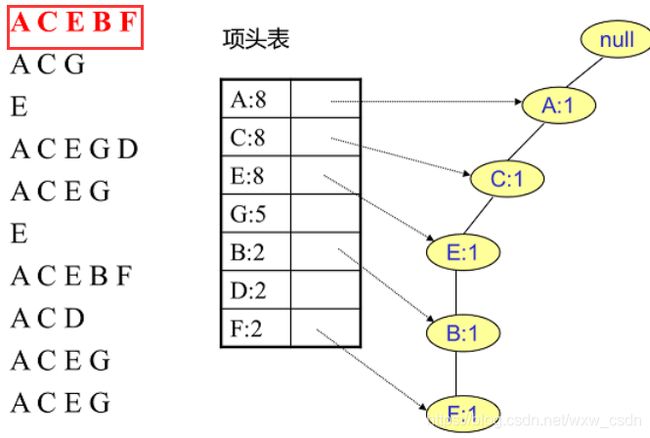
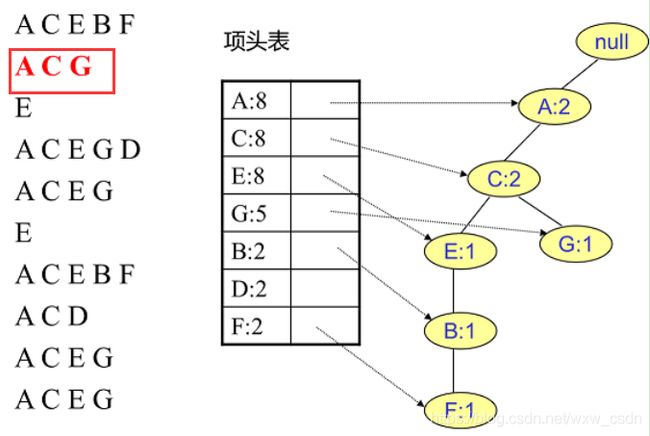
1 根据设定的支持度阈值筛选频繁 1 项集，构建项头表，然后对原始数据集去除非频繁 1 项集，并按照项头表顺序排列各项。

2 构建 FP-Tree：按照排序之后的数据集逐条构建

最后构建的树结构如下：

3 根据树结构，挖掘频繁项集

1 从 FP 树中获得条件模式基
2 利用条件模式基，构建一个条件 FP 树
3 迭代重复步骤 (1) 和步骤 (2)，直到树包含一个元素项为止

条件模式基：介于所查找项头表中的元素项与根节点之间的所有节点构成的链表，且各节点的个数设置为所查找元素的个数。
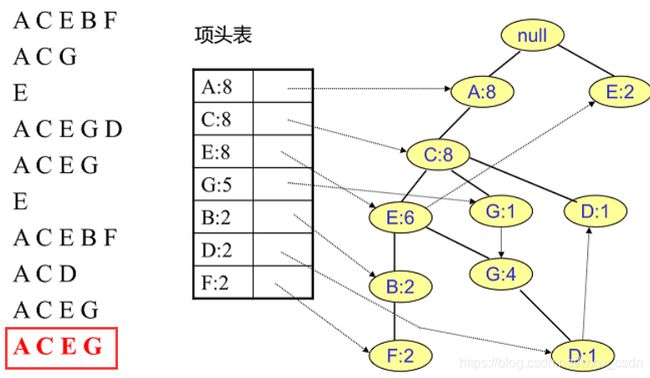
只有一个条件模式基的情况，可以根据条件模式基较容易的构建频繁 k 项集，如下图先构建 F 的频繁 2 项集 {A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}；然后构建频繁三项集 {A:2,C:2,F:2}，{A:2,E:2,F:2} 等，直到构建最大的频繁 5 项集 {A:2,C:2,E:2,B:2,F:2}。

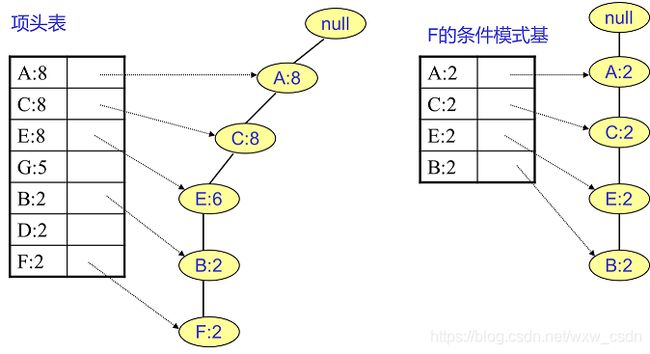
不止一个条件模式基的情况，如下图 D 有两个条件模式基 {A:1,C:1,E:1,G:1} 与 {A:1,C:1}，通过构建条件 FP 树剔除非频繁项集，最终构建的条件模式基为 {A:2,C:2}，再利用挖掘的条件模式基构建频繁项集。

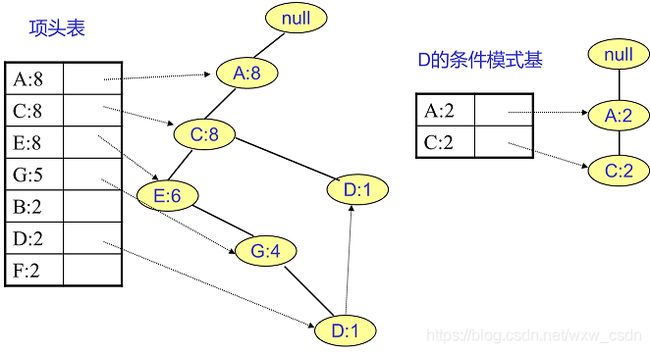
对于上例中的 A 来说，其条件模式基为空，至此频繁项集挖掘结束。

2 python中的实现

由于常用的机器学习库 Sklearn 中没有关联分析可以直接调用的模块，在 python 中 Apriori 算法的具体实现可以参考Eastmount大神的博文，修改之后 python3 的代码如下：

def loadDataSet():
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

dataSet = loadDataSet()
# 获取候选1项集，dataSet为事务集。返回一个list，每个元素都是set集合
def createC1(dataSet):
    C1 = []   # 元素个数为1的项集（非频繁项集，因为还没有同最小支持度比较）
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()  # 这里排序是为了，生成新的候选集时可以直接认为两个n项候选集前面的部分相同
    # 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在，所以要将候选1项集的每一个元素都转化为一个单独的集合。
    return list(map(frozenset, C1))   #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合（frozenset，Python中的数据结构）
    
# 找出候选集中的频繁项集
# dataSet为全部数据集，Ck为大小为k（包含k个元素）的候选项集，minSupport为设定的最小支持度
def scanD(dataSet, Ck, minSupport):
    ssCnt = {}   # 记录每个候选项的个数
    for tid in dataSet:
        for can in Ck:
            if can.issubset(tid):
                ssCnt[can] = ssCnt.get(can, 0) + 1   # 计算每一个项集出现的频率
    numItems = float(len(dataSet))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            retList.insert(0, key)  #将频繁项集插入返回列表的首部
        supportData[key] = support
    return retList, supportData   #retList为在Ck中找出的频繁项集（支持度大于minSupport的），supportData记录各频繁项集的支持度

# 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。
def aprioriGen(Lk, k):
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            # 前k-1项相同时，才将两个集合合并，合并后才能生成k+1项
            L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]   # 先把不可变的集合转换成列表，再取出两个集合的前k-1个元素
            L1.sort(); L2.sort()
            if L1 == L2:
                retList.append(Lk[i] | Lk[j]) #集合中的并集运算
    return retList

# 获取事务集中的所有的频繁项集
# Ck表示项数为k的候选项集，最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集，supK为其支持度，Lk和supK由scanD()函数通过Ck计算而来。
def apriori(dataSet, minSupport=0.5):
    C1 = createC1(dataSet)  # 从事务集中获取候选1项集
    D = list(map(set, dataSet))  # 将事务集的每个元素转化为集合
    L1, supportData = scanD(D, C1, minSupport)  # 获取频繁1项集和对应的支持度
    L = [L1]  # L用来存储所有的频繁项集
    k = 2
    while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集
        Ck = aprioriGen(L[k-2], k)   # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集
        Lk, supK = scanD(D, Ck, minSupport)  # Lk表示项数为k的频繁项集，supK为其支持度
        L.append(Lk);supportData.update(supK)  # 添加新频繁项集和他们的支持度
        k += 1
    return L, supportData

dataSet = loadDataSet()  # 获取事务集。每个元素都是列表
# C1 = createC1(dataSet)  # 获取候选1项集。每个元素都是集合
# D = list(map(set, dataSet))  # 转化事务集的形式，每个元素都转化为集合。
# L1, suppDat = scanD(D, C1, 0.5)
# print(L1,suppDat)

L, suppData = apriori(dataSet,minSupport=0.7)
print(L,suppData)

在 python 中 FP-Growth 算法的具体实现可以参考这篇文章。

# FP树类
class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue  #节点元素名称，在构造时初始化为给定值
        self.count = numOccur   # 出现次数，在构造时初始化为给定值
        self.nodeLink = None   # 指向下一个相似节点的指针，默认为None
        self.parent = parentNode   # 指向父节点的指针，在构造时初始化为给定值
        self.children = {}  # 指向子节点的字典，以子节点的元素名称为键，指向子节点的指针为值，初始化为空字典

    # 增加节点的出现次数值
    def inc(self, numOccur):
        self.count += numOccur

    # 输出节点和子节点的FP树结构
    def disp(self, ind=1):
        print(' ' * ind, self.name, ' ', self.count)
        for child in self.children.values():
            child.disp(ind + 1)

# =======================================================构建FP树==================================================
# 对不是第一个出现的节点，更新头指针块。就是添加到相似元素链表的尾部
def updateHeader(nodeToTest, targetNode):
    while (nodeToTest.nodeLink != None):
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode

# 根据一个排序过滤后的频繁项更新FP树
def updateTree(items, inTree, headerTable, count):
    if items[0] in inTree.children:
        # 有该元素项时计数值+1
        inTree.children[items[0]].inc(count)
    else:
        # 没有这个元素项时创建一个新节点
        inTree.children[items[0]] = treeNode(items[0], count, inTree)
        # 更新头指针表或前一个相似元素项节点的指针指向新节点
        if headerTable[items[0]][1] == None:  # 如果是第一次出现，则在头指针表中增加对该节点的指向
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:
            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])

    if len(items) > 1:
        # 对剩下的元素项迭代调用updateTree函数
        updateTree(items[1::], inTree.children[items[0]], headerTable, count)

# 主程序。创建FP树。dataSet为事务集，为一个字典，键为每个事物，值为该事物出现的次数。minSup为最低支持度
def createTree(dataSet, minSup=1):
    # 第一次遍历数据集，创建头指针表
    headerTable = {}
    for trans in dataSet:
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
    # 移除不满足最小支持度的元素项
    keys = list(headerTable.keys()) # 因为字典要求在迭代中不能修改，所以转化为列表
    for k in keys:
        if headerTable[k] < minSup:
            del(headerTable[k])
    # 空元素集，返回空
    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0:
        return None, None
    # 增加一个数据项，用于存放指向相似元素项指针
    for k in headerTable:
        headerTable[k] = [headerTable[k], None]  # 每个键的值，第一个为个数，第二个为下一个节点的位置
    retTree = treeNode('Null Set', 1, None) # 创建只包含空集的根节点
    # 第二次遍历数据集，创建FP树
    for tranSet, count in dataSet.items():
        localD = {} # 记录频繁1项集的全局频率，用于排序
        for item in tranSet:
            if item in freqItemSet:   # 只考虑频繁项
                localD[item] = headerTable[item][0] # 注意这个[0]，因为之前加过一个数据项
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] # 排序
            updateTree(orderedItems, retTree, headerTable, count) # 更新FP树
    return retTree, headerTable

# =================================================查找元素条件模式基===============================================

# 直接修改prefixPath的值，将当前节点leafNode添加到prefixPath的末尾，然后递归添加其父节点。
# prefixPath就是一条从treeNode（包括treeNode）到根节点（不包括根节点）的路径
def ascendTree(leafNode, prefixPath):
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)

# 为给定元素项生成一个条件模式基（前缀路径）。basePet表示输入的频繁项，treeNode为当前FP树中对应的第一个节点
# 函数返回值即为条件模式基condPats，用一个字典表示，键为前缀路径，值为计数值。
def findPrefixPath(basePat, treeNode):
    condPats = {}  # 存储条件模式基
    while treeNode != None:
        prefixPath = []  # 用于存储前缀路径
        ascendTree(treeNode, prefixPath)  # 生成前缀路径
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count  # 出现的数量就是当前叶子节点的数量
        treeNode = treeNode.nodeLink  # 遍历下一个相同元素
    return condPats

# =================================================递归查找频繁项集===============================================
# 根据事务集获取FP树和频繁项。
# 遍历频繁项，生成每个频繁项的条件FP树和条件FP树的频繁项
# 这样每个频繁项与他条件FP树的频繁项都构成了频繁项集

# inTree和headerTable是由createTree()函数生成的事务集的FP树。
# minSup表示最小支持度。
# preFix请传入一个空集合（set([])），将在函数中用于保存当前前缀。
# freqItemList请传入一个空列表（[]），将用来储存生成的频繁项集。
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    # 对频繁项按出现的数量进行排序进行排序
    sorted_headerTable = sorted(headerTable.items(), key=lambda p: p[1][0])  #返回重新排序的列表。每个元素是一个元组，[（key,[num,treeNode],()）
    bigL = [v[0] for v in sorted_headerTable]  # 获取频繁项
    for basePat in bigL:
        newFreqSet = preFix.copy()  # 新的频繁项集
        newFreqSet.add(basePat)     # 当前前缀添加一个新元素
        freqItemList.append(newFreqSet)  # 所有的频繁项集列表
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])  # 获取条件模式基。就是basePat元素的所有前缀路径。它像一个新的事务集
        myCondTree, myHead = createTree(condPattBases, minSup)  # 创建条件FP树

        if myHead != None:
            # 用于测试
            print('conditional tree for:', newFreqSet)
            myCondTree.disp()
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)  # 递归直到不再有元素

# 生成数据集
def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat

# 将数据集转化为目标格式
def createInitSet(dataSet):
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1
    return retDict

minSup =3
simpDat = loadSimpDat()  # 加载数据集
initSet = createInitSet(simpDat)  # 转化为符合格式的事务集
myFPtree, myHeaderTab = createTree(initSet, minSup)  # 形成FP树
# myFPtree.disp()  # 打印树

freqItems = []  # 用于存储频繁项集
mineTree(myFPtree, myHeaderTab, minSup, set([]), freqItems)  # 获取频繁项集
print(freqItems)  # 打印频繁项集

目前在 Python 中，可以实现关联分析的包主要有：

• pymining：根据 Apriori 算法进行关联规则挖掘，目前不再维护；
• Orange3 的关联规则库：根据 FP-Growth 算法进行关联规则挖掘；
• fp_growth ：根据 FP-Growth 算法进行关联规则挖掘，但采用的是 Python2 的语法实现，具体可以参考这篇文章。

其中 Orange3 的关联规则输入支持布尔类型、字符串类型两种，主要包括三个函数的调用：

• frequent_itemsets()：获取频繁项集
• association_rules()：获取关联规则
• rules_stats()： 生成关联规则，并在内存中清除存储的关联规则结果。

各函数的主要参数如下：

fpgrowth.frequent_itemsets(X, min_support=0.2)

• X：代表输入的数据集，类型可以为：list or numpy.ndarray or scipy.sparse.spmatrix or iterator；
• min_support：类型为 0-1 间的数或者大于1的整数，代表关联规则设置的最小支持度，默认为 0.2；
• 返回频繁项集（itemset (frozenset)）与支持度（support (int) ）。

fpgrowth.association_rules(itemsets, min_confidence, itemset=None)

• itemsets：频繁项集
• min_confidence：最小置信度
• itemset：关联规则的初始值
• 返回关联规则、支持度、置信度

fpgrowth.rules_stats(rules, itemsets, n_examples)

• rules:关联规则
• itemsets：频繁项集
• n_examples：事例的总数目
  返回关联规则、支持度、置信度、支持度等关联规则评价指标，最后清空存储的关联规则。

import orangecontrib.associate.fpgrowth as ftp

#事例总条数，并生成布尔型数组
N = 30
X = np.random.random((N, 50)) > 0.9
# 获取频繁项集
itemsets = dict(ftp.frequent_itemsets(X, 0.1))
# 获取关联规则
rules = ftp.association_rules(itemsets, 0.6)
# 生成关联规则并清空rules
list(ftp.rules_stats(rules, itemsets, N))

3 参考资料

例子参考博客：https://www.cnblogs.com/bigmonkey/p/7405555.html