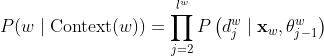基于分层softmax的CBoW模型详解
入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。
✨word2vector系列展示✨
一、CBOW
1、朴素CBOW模型
word2vector之CBoW模型详解_tt丫的博客-CSDN博客
2、基于分层softmax的CBOW模型
本篇
3、基于高频词抽样+负采样的CBOW模型
基于高频词抽样+负采样的CBOW模型_tt丫的博客-CSDN博客
二、Skip_Gram
word2vector之Skip_Gram模型详解_tt丫的博客-CSDN博客
（关于Skip_Gram的分层softmax和负采样，与CBOW类似）
目录
一、朴素CBoW模型介绍及代码实现
二、使用分层softmax改进CBoW模型的原因
三、背景知识——哈夫曼树和逻辑回归Sigmoid函数
1、哈夫曼树
2、逻辑回归Sigmoid函数
四、改进后的网络分析
1、改进后的网络结构图（与朴素CBoW模型进行对比）
2、层次级结构内容分析
3、细说OUTPUT的这棵哈夫曼树
五、分层softmax下的梯度计算
1、例子下的问题描述
2、利用sigmoid函数模拟走到正负类的概率
3、符号定义预先说明
4、二分类问题下的目标函数
5、梯度求解
六、采用分层softmax的缺点
一、朴素CBoW模型介绍及代码实现
word2vector之CBoW模型详解_tt丫的博客-CSDN博客
二、使用分层softmax改进CBoW模型的原因
CBoW模型是用上下文X来预测中间词Y，那么其输出层（输出是1 ∗ V的向量）有V个神经元，我们对这V个神经元一开始是等同对待的，但是如果V的数值非常大，等同对待，会导致效率过低，计算量过大。
三、背景知识——哈夫曼树和逻辑回归Sigmoid函数
1、哈夫曼树
python数据结构之树（3）—— 哈夫曼树_tt丫的博客-CSDN博客
2、逻辑回归Sigmoid函数
Sigmoid函数公式为：
图像：
特点
（1）当x趋近于正无穷时，g(x)趋近于1；当x趋近于负无穷时，g(x)趋近于0；
（2）
推导过程：
四、改进后的网络分析
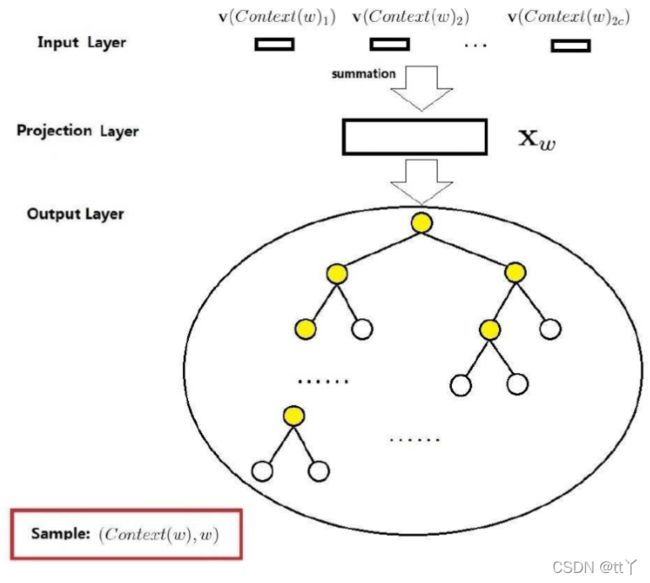
1、改进后的网络结构图（与朴素CBoW模型进行对比）
上图为改进后的网络结构图，下图为朴素CBoW模型网络结构图（图片来源于网络，侵权立删）
注：图中的2c相当于我接下来说的C
2、层次级结构内容分析
INPUT：C个词的词向量（没变）
Projection：将输入层的C个向量做求和累加，即
OUTPUT：去掉前面的隐藏层，对应替换成一棵哈夫曼树。
3、细说OUTPUT的这棵哈夫曼树
原本CBoW模型中输出层最后不是有对1 ∗ V的向量做softmax处理嘛。
这里就是为了避免要计算所有词（V个）的softmax概率，采取了用哈夫曼树来代替从隐藏层到输出softmax层的映射。
这样看来，哈夫曼树的所有内部节点就像之前神经网络Hidden Layer中的神经元。
哈夫曼树以对应Projection的输出词向量为根节点，以这V个词（即类似于之前神经网络softmax输出层的神经元）为叶子结点，以各词在语料中出现的词频当权重。
那么根据哈夫曼树的性质：越靠近根节点的地方，词频（权重）越高，我们可以更快的使用到这个词，相反的越靠近叶节点的地方，词频越低；这样就提高了训练的效率。
在霍夫曼树中，隐藏层到输出层的softmax映射不是一下子完成的，而是沿着霍夫曼树一步步完成的，因此这种softmax取名为”Hierarchical softmax”，即分层softmax。
五、分层softmax下的梯度计算
替换成哈夫曼树后的P(w|Context(w))该如何定义呢？
1、例子下的问题描述
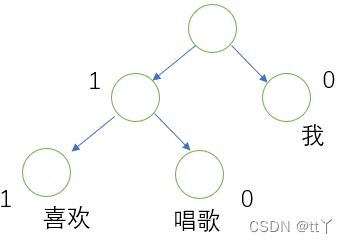
比如说这棵树长这样：
那么以“唱歌”为例子。
从根节点到“唱歌”，需要经历2次分支，每一次分支的经历都可以看作是进行了一次二分类。
既然是二分类问题，我们需要给每个非叶子结点的左右孩子结点指定一个类别（正类负类）。这里我们采用二元逻辑回归的方法——即规定沿左子树走是负类(哈夫曼编码1)，沿右子树走是正类(哈夫曼编码0)。
2、利用sigmoid函数模拟走到正负类的概率
判别正类和负类的方法是使用sigmoid函数，如下所示：
其中 
是当前内部节点的词向量，而 θ 则是我们需要从训练样本中求出的逻辑回归的模型参数
3、符号定义预先说明
接下来我们先说一下一些符号的定义：
：从根结点出发到达词w对应的叶子结点的路径
：路径
：路径
：表示路径
4、二分类问题下的目标函数
因为每次分支的选择都是一个二分类问题，所以得到以下公式：
简单来说：它的意义就是那种从根节点走到“唱歌”这个结点的概率
即根节点出来后走1的概率再乘上从当前1结点走到下面0结点的概率（1，0看上面的图）
又因为我们采用了二元逻辑回归的方法来定义这些个概率，所以有：
因此，对于一个输出词w来说，
5、梯度求解
这里我们使用了随机梯度上升法，即没有把所有样本的似然概率乘起来得到真正的训练集最大似然概率，仅仅每次只用一个样本来更新梯度，这样可以减少梯度计算量。
所以对上述公式左右取对数，得
我们需要更新的就是
以及模型参数 
对
由求导法则和sigmoid函数的性质得到以下求
那么
![\theta_{j-1}^{w}:=\theta_{j-1}^{w}+\eta\left[1-d_{j}^{w}-g\left(\mathbf{x}_{w}^{T} \theta_{j-1}^{w}\right)\right] \mathbf{x}_{w}](http://img.e-com-net.com/image/info8/c0aeddd807f646fa8eba6dbb1c0d3bd7.gif){kind=small}
对
同理可得：
而我们最终是要求词典 V 中每个词的词向量，这里的是Context(w)中各词词向量的累加。
因此我们对
进行更新
这样就完整完成了反向传播啦~
六、采用分层softmax的缺点
使用哈夫曼树来代替传统的神经网络，确实可以提高模型训练的效率。但是如果我们的训练样本里的中心词w是一个很生僻的词，那么就得在哈夫曼树中向下走很久了 ，就会很麻烦。
欢迎大家在评论区批评指正，谢谢啦~