python实现卷积操作

0. 前言

卷积神经网络与全连接神经网络类似, 可以理解成一种变换, 这种变换一般由卷积、池化、激活函数等一系列操作组合而成. 本文就“卷积”部分稍作介绍.

1. 卷积介绍

卷积可以看作是输入和卷积核之间的内积运算, 是两个实质函数之间的一种数学运算. 在卷积运算中, 通常使用卷积核将输入数据进行卷积运算得到的输出作为特征映射, 每个卷积核可获得一个特征映射.
如图所示, 一张大小为$5\times 5\times 3$的图片经过零填充后, 大小变为 $7\times 7\times 3$. 使用两个大小为$3\times 3\times 3$的卷积核进行步长为$1$的卷积运算, 最后得到一个大小为$3\times 3\times 2$的 feature map.

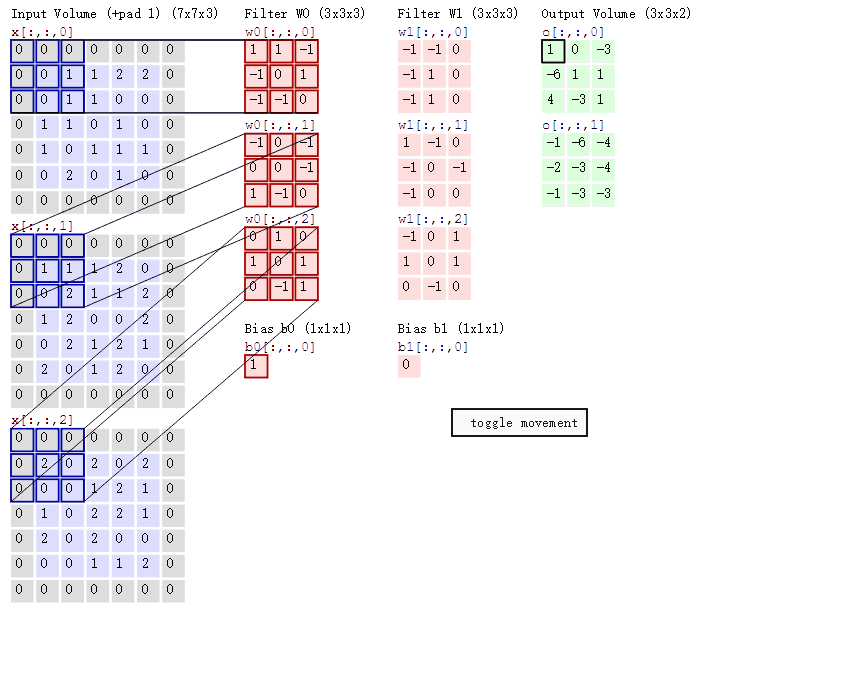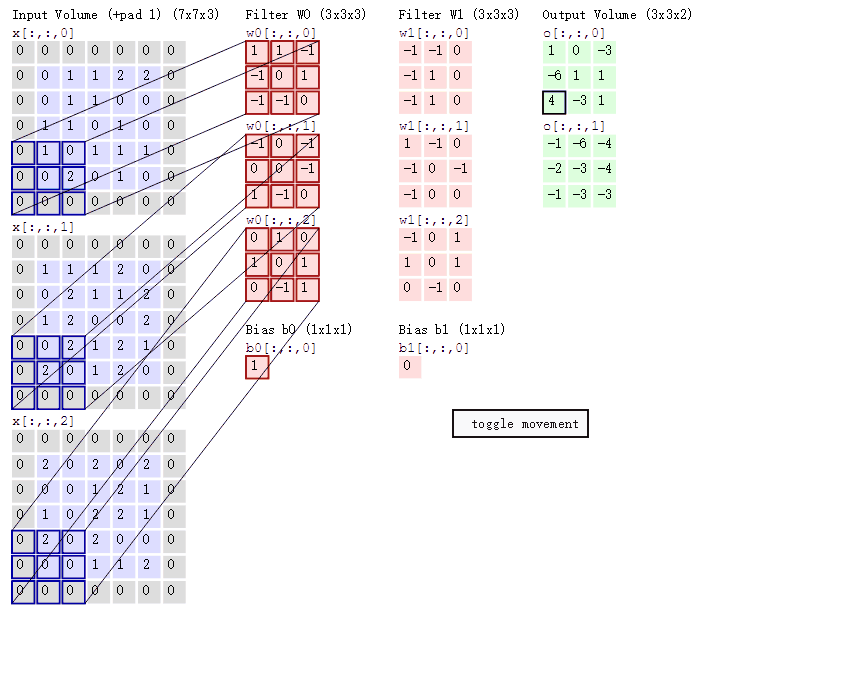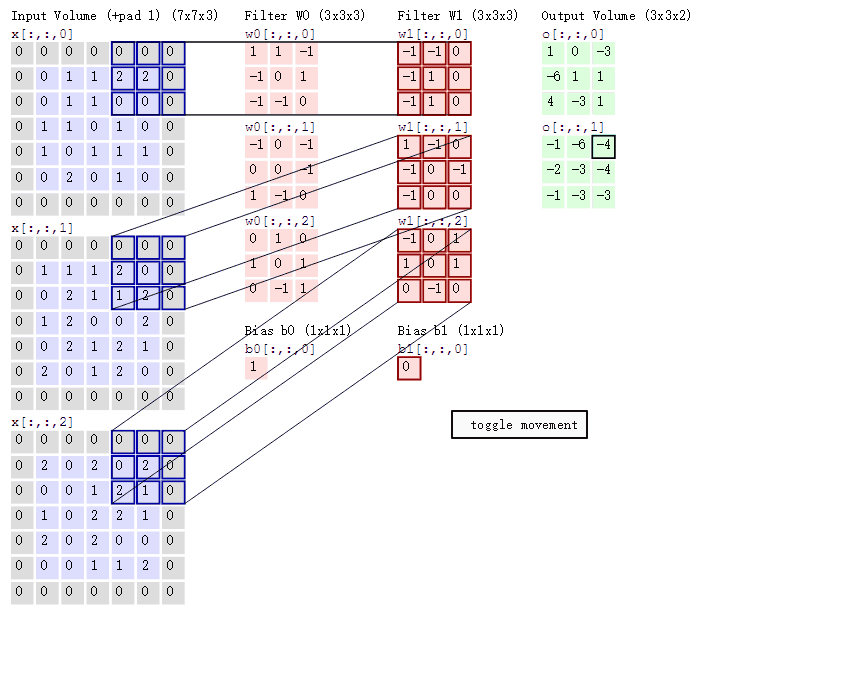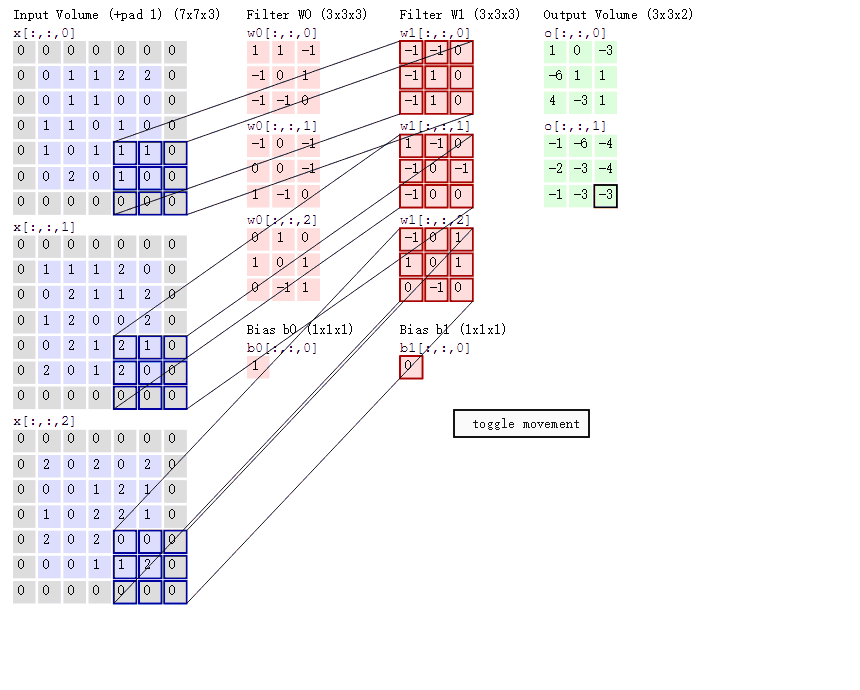
可以看到, 卷积核在图片所对应的矩阵中滑动. 每滑动到一个位置, 将对应数字相乘并求和, 得到一个特征图矩阵的元素.
注意, 卷积核每次滑动的步长为$1$, 才能滑动到矩阵的边缘部分.

1.1 卷积的三种模式:

1. FULL
   
   橙色部分为image, 蓝色部分为filter. full模式的意思是, 从filter和image刚相交开始做卷积, 白色部分为填0.

2. SAME
   
   当filter的中心与image的边角重合时, 开始做卷积运算.

3. VALID
   
   当filter全部在image里面的时候，进行卷积运算.

1.2 feature map 公式计算

首先定义如下参数,

• 输入大小 $B\times H\times W\times C$
• 卷积核大小 $b\times h\times w\times C$
• 步长 $S$

1.FULL:
输出大小 $B\times \lfloor \frac{H+h+1}{S}\rfloor \times \lfloor \frac{W+w+1}{S}\rfloor \times b$

2.SAME:
输出大小 $B\times \lfloor \frac{H}{S}\rfloor \times \lfloor \frac{W}{S}\rfloor \times b$

3.VALID:
输出大小 $B\times \lfloor \frac{H-h+1}{S}\rfloor \times \lfloor \frac{W-w+1}{S}\rfloor \times b$

Tensorflow中的卷积有“same”和“valid”两种模式
Pytorch中可以直接通过设置参数“padding"来控制零层的填充.

同样, 我们可以基于零层填充的圈数$P$, 得到我们的另一个计算公式:
输出大小 $B\times \lfloor \frac{H-h+2P}{S}+1\rfloor \times \lfloor \frac{W-w+2P}{S}+1\rfloor \times b$

2. 代码实现

import numpy as np
import math


class Conv2D():
    def __init__(self, inputShape, outputChannel, kernelSize, stride=1, method=""):
        self.height = inputShape[1]
        self.width = inputShape[2]
        self.inputChannel = inputShape[-1]
        self.outputChannel = outputChannel
        self.batchSize = inputShape[0]
        self.stride = stride
        self.kernelSize = kernelSize
        self.method = method

        # initial the parameters of the kernel, do not initial them as zero
        self.weights = np.random.standard_normal([self.inputChannel, kernelSize, kernelSize, self.outputChannel])
        self.bias = np.random.standard_normal(self.outputChannel)

        # the shape of the output
        """
        # This part has some problems
        
        if method == "FULL":
            self.output = np.zeros(inputShape[0],
                                   math.floor((inputShape[1] - kernelSize + 2 * (kernelSize - 1)) / self.stride) + 1,
                                   math.floor((inputShape[2] - kernelSize + 2 * (kernelSize - 1)) / self.stride) + 1,
                                   self.outputChannel)  
        """

        if method == "SAME":
            self.output = np.zeros(
                (self.batchSize, math.floor(self.height / self.stride), math.floor(self.width / self.stride),
                 self.outputChannel))

        if method == "VALID":
            self.output = np.zeros([self.batchSize, math.floor((self.height - kernelSize + 1) / self.stride),
                                    math.floor((self.width - kernelSize + 1) / self.stride),
                                    self.outputChannel])

    def forward(self, x):
        weights = self.weights.reshape([-1, self.outputChannel])  # shape: [(h*w),#]

        # Filling operation
        # Note that: x is 4-dimensional.
        """
        
        if self.method == "FULL":
            x = np.pad(x, (
                (0, 0), (self.kernelSize - 1, self.kernelSize - 1), (self.kernelSize - 1, self.kernelSize - 1),
                (0, 0)), 'constant', constant_values=0)

        """
        if self.method == "SAME":
            x = np.pad(x, (
                (0, 0), (self.kernelSize // 2, self.kernelSize // 2), (self.kernelSize // 2, self.kernelSize // 2),
                (0, 0)), 'constant', constant_values=0)

        convOut = np.zeros(self.output.shape)

        for i in range(self.batchSize):
            img_i = x[i]
            # img_i = x[i][np.newaxis, :, :, :]
            colImage_i = self.im2col(img_i, self.kernelSize, self.stride)
            convOut[i] = np.reshape(np.dot(colImage_i, weights) + self.bias, self.output[0].shape)
        return convOut

    # im2col function
    def im2col(self, image, kernelSize, stride):
        imageCol = []
        for i in range(0, image.shape[0] - kernelSize + 1, stride):
            for j in range(0, image.shape[1] - kernelSize + 1, stride):
                col = image[i:i + kernelSize, j:j + kernelSize, :].reshape([-1])
                # col = image[:, i:i + kernelSize, j:j + kernelSize, :].reshape([-1])  # Do not use .view([-1])
                imageCol.append(col)
        imageCol = np.array(imageCol)  # shape: [(h*w),(c*h*w)] kernel's height, width and channels
        return imageCol


# Test part

inputData = np.random.random((4, 5, 5, 3))
print("inputShape: ", inputData.shape)
kernel = list([3, 3, 32])
print("kernel size: ", kernel)
conv2d = Conv2D(inputShape=inputData.shape, outputChannel=kernel[2], kernelSize=kernel[0], stride=1, method='VALID')
outputData = conv2d.forward(inputData)
print("outputShape: ", outputData.shape)

本文形状的命名方式为$(\text{batchsize},\text{height},\text{width},\text{channels})$, 与Tensorflow中命名一致.
与Pytorch中的命名为$(\text{batchsize},\text{channels},\text{height},\text{width})$有所不同.

重点:
由于图片转换后得到的矩阵为4维矩阵, 我们在进行计算处理的过程中会对矩阵进行降维处理; 并且在进行矩阵乘法时, 也要注意两矩阵是否满足矩阵乘法的条件.

---

参考资料:
https://www.bilibili.com/video/BV1VV411478E
https://www.bilibili.com/video/BV1m34y1m7TD
https://zhuanlan.zhihu.com/p/63974249
https://blog.csdn.net/god_frey09/article/details/105188005
https://blog.csdn.net/v_JULY_v/article/details/51812459
https://www.jianshu.com/p/46b6615a7251
https://blog.csdn.net/dwyane12138/article/details/78449898