Faster R-CNN 学习

一、整体架构

参考https://www.cnblogs.com/wangyong/p/8513563.html
一文教你如何用PyTorch构建 Faster RCNN

二、网络结构

现在，通过上图开始逐层分析

2.1、Conv layers

Faster RCNN首先是支持输入任意大小的图片的，比如上图中输入的PQ，进入网络之前对图片进行了规整化尺度的设定，如可设定图像短边不超过600，图像长边不超过1000，我们可以假定MN=1000*600（如果图片少于该尺寸，可以边缘补0，即图像会有黑色边缘）

（1）13个conv层：kernel_size=3,pad=1,stride=1;

卷积公式：
所以，conv层不会改变图片大小（即：输入的图片大小=输出的图片大小）

（2）13个relu层：激活函数，不改变图片大小

（3）4个pooling层：kernel_size=2,stride=2；pooling层会让输出图片是输入图片的1/2
经过Conv layers，图片大小变成(M/16)(N/16)，即：6040(1000/16≈60,600/16≈40)；则，Feature Map就是6040512-d(注：VGG16是512-d,ZF是256-d)，表示特征图的大小为60*40，数量为512
把feature map的点映射回原图（参看：原始图片中的ROI如何映射到到feature map?）
如何计算CNN感受野
如果原图输入是224x224，对于conv5出来后的输出，是13x13x256的，可以理解成有256个这样的filte（空间金字塔滤波），每个filter对应一张13x13的activation map.如果像上图那样将activation map pooling成4x4 2x2 1x1三张子图，做max pooling后，出来的特征就是固定长度的(16+4+1)x256那么多的维度了.如果原图的输入不是224x224，出来的特征依然是(16+4+1)x256

2.2 RPN(Region Proposal Networks)

RPN网络代码实现说明Caffe

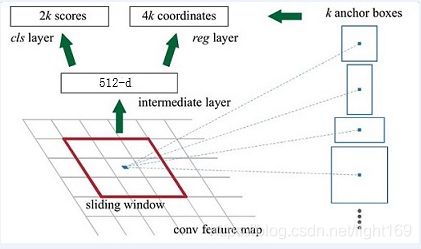
RPN的本质是 “ 基于滑窗的无类别obejct检测器 ”

上图4展示了RPN网络的具体结构。可以看到RPN网络实际分为2条线，上面一条通过softmax分类anchors获得positive和negative分类，下面一条用于计算对于anchors的bounding box regression偏移量，以获得精确的proposal。而最后的Proposal层则负责综合positive anchors和对应bounding box regression偏移量获取proposals，同时剔除太小和超出边界的proposals。其实整个网络到了Proposal Layer这里，就完成了相当于目标定位的功能。
Feature Map进入RPN后，先经过一次33的卷积，同样，特征图大小依然是6040,数量512，这样做的目的应该是进一步集中特征信息，接着看到两个全卷积,即kernel_size=1*1,p=0,stride=1;

如上图中标识：

① rpn_cls：60 * 40 * 512-d ⊕ 1 * 1 * 512 * 18 ==> 60 * 40 * 9 * 2
逐像素对其9个Anchor box进行二分类, 用于判定该proposal是前景还是背景。
说明1 * 1 * 512 为1X1X512 卷积核，512是上层输入的通道数。18为卷积核的个数，18个卷积核生成下一层的9*2=18个通道

② rpn_bbox：60 * 40 * 512-d ⊕ 1 * 1 * 512 * 36==>60 * 40 * 9 * 4
逐像素得到其9个Anchor box四个坐标信息（其实是偏移量，后面介绍）, 用于预测proposal的中心锚点对应的proposal的坐标x，y和宽高w，h；

如下图所示：

2.3 Anchors的生成规则

经过Conv layers后，图片大小变成了原来的1/16，令feat_stride=16，在生成Anchors时，我们先定义一个base_anchor，大小为1616的box(因为特征图(6040)上的一个点，可以对应到原图（1000600）上一个1616大小的区域)，源码中转化为[0,0,15,15]的数组，参数ratios=[0.5, 1, 2]scales=[8, 16, 32]

先看[0,0,15,15],面积保持不变，长、宽比分别为[0.5, 1, 2]是产生的Anchors box

如果经过scales变化，即长、宽分别均为 (168=128)、(1616=256)、(16*32=512)，对应anchor box如图

综合以上两种变换，最后生成9个Anchor box

所以，最终base_anchor=[0,0,15,15]生成的9个Anchor box坐标如下：

[[ -84.  -40.   99.   55.]
[-176.  -88.  191.  103.]
[-360. -184.  375.  199.]
[ -56.  -56.   71.   71.]
[-120. -120.  135.  135.]
[-248. -248.  263.  263.]
[ -36.  -80.   51.   95.]
[ -80. -168.   95.  183.]
[-168. -344.  183.  359.]]

特征图大小为6040，所以会一共生成6040*9=21600个Anchor box

源码中，通过width:(0_{60)*16,height(0}40)*16建立shift偏移量数组，再和base_ancho基准坐标数组累加，得到特征图上所有像素对应的Anchors的坐标值，是一个[216000,4]的数组

2.4 边界框回归原理与实现方法

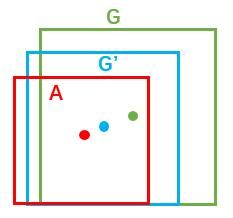
对于窗口一般使用四维向量 (x, y, w, h)表示，分别表示窗口的中心点坐标和宽高。对于图 11，红色的框A代表原始的Foreground Anchors，绿色的框G代表目标的GT，我们的目标是寻找一种关系，使得输入原始的anchor A经过映射得到一个跟真实窗口G更接近的回归窗口G’，即：

• 给定：$anchorA=(A_x,A_y,A_w,A_h)$ 和 $GT=[G_x,G_y,G_w,G_h]$

• 寻找一种变换$F$，使得： $F(A_x,A_y,A_w,A_h)=(G_x^{{}^{\prime }},G_y^{{}^{\prime }},G_w^{{}^{\prime }},G_h^{{}^{\prime }})$ 其中$(G_x^{{}^{\prime }},G_y^{{}^{\prime }},G_w^{{}^{\prime }},G_h^{{}^{\prime }})\approx (G_x,G_y,G_w,G_h)$
  那么经过何种变换F才能从anchor A变为G’呢？ 比较简单的思路就是:

先做平移

再做缩放

观察上面4个公式发现，需要学习的是 $d_x(A),d_y(A),d_w(A),d_h(A)$ 这四个变换。当输入的anchor A与GT相差较小时，可以认为这种变换是一种线性变换， 那么就可以用线性回归来建模对窗口进行微调（注意，只有当anchors A和GT比较接近时，才能使用线性回归模型，否则就是复杂的非线性问题了）。
接下来的问题就是如何通过线性回归获得 $d_x(A),d_y(A),d_w(A),d_h(A)$ 了。
线性回归就是给定输入的特征向量X, 学习一组参数W, 使得经过线性回归后的值跟真实值Y非常接近，即Y=WX。对于该问题，输入X是cnn feature map，定义为Φ；同时还有训练传入A与GT之间的变换量，即$(t_x,t_y,t_w,t_h)$。输出是$d_x(A),d_y(A),d_w(A),d_h(A)$四个变换。那么目标函数可以表示为：

其中Φ(A)是对应anchor的feature map组成的特征向量，w是需要学习的参数，d(A)是得到的预测值（*表示 x，y，w，h，也就是每一个变换对应一个上述目标函数）。为了让预测值$(t_x,t_y,t_w,t_h)$与真实值差距最小，设计损失函数：

函数优化目标为：

需要说明，只有在GT与需要回归框位置比较接近时，才可近似认为上述线性变换成立。
说完原理，对应于Faster RCNN原文，foreground anchor与ground truth之间的平移量 $(t_x,t_y)$与尺度因子 $(t_w,t_h)$ 如下：

对于训练bouding box regression网络回归分支，输入是cnn feature Φ，监督信号是Anchor与GT的差距 $(t_x,t_y,t_w,t_h)$，即训练目标是：
输入 Φ的情况下使网络输出与监督信号尽可能接近。

• 那么当bouding box regression工作时，再输入Φ时，回归网络分支的输出就是每个Anchor的平移量和变换尺度
  $(t_x,t_y,t_w,t_h)$，显然即可用来修正Anchor位置了。

2.5 损失函数

2.5.1 Fast R-CNN

Fast R-CNN网络有两个同级输出层（cls score和bbox_prdict层），都是全连接层，称为multi-task。

① clsscore层：用于分类，输出k+1维数组p，表示属于k类和背景的概率。对每个RoI（Region of Interesting）输出离散型概率分布

通常，p由k+1类的全连接层利用softmax计算得出。

② bbox_prdict层：用于调整候选区域位置，输出bounding box回归的位移，输出4*K维数组t，表示分别属于k类时，应该平移缩放的参数。

k表示类别的索引，$t_x^k,t_y^k$是指相对于objectproposal尺度不变的平移，$t_w^k,t_h^k$是指对数空间中相对于objectproposal的高与宽。

loss_cls层评估分类损失函数。由真实分类u对应的概率决定：

loss_bbox评估检测框定位的损失函数。比较真实分类对应的预测平移缩放参数
和真实平移缩放参数为
的差别：

其中，smooth L1损失函数为：

smooth L1损失函数曲线如下图9所示，作者这样设置的目的是想让loss对于离群点更加鲁棒，相比于L2损失函数，其对离群点、异常值（outlier）不敏感，可控制梯度的量级使训练时不容易跑飞。

图9 smoothL1损失函数曲线

最后总损失为（两者加权和，如果分类为背景则不考虑定位损失）：

规定u=0为背景类（也就是负标签），那么艾弗森括号指数函数[u≥1]表示背景候选区域即负样本不参与回归损失，不需要对候选区域进行回归操作。λ控制分类损失和回归损失的平衡。Fast R-CNN论文中，所有实验λ=1。

艾弗森括号指数函数为：

2.5.2 Faster R-CNN损失函数

参考：【Faster RCNN】损失函数理解
faster rcnn中 损失函数(一)——softmax,softmax loss.
遵循multi-task loss定义，最小化目标函数，FasterR-CNN中对一个图像的函数定义为：

i表示第i个anchor，当anchor是正样本时 $p_i^{\ast }$ =1 ，是负样本则=0 。 $t_i^{\ast }$表示 一个与正样本anchor 相关的ground true box 坐标 （每个正样本anchor 只可能对应一个ground true box： 一个正样本anchor 与某个grand true box对应，那么该anchor与ground true box 的IOU要么是所有anchor中最大，要么大于0.7）
x,y,w,h分别表示box的中心坐标和宽高，$x,x_a,x^{\ast }$分别表示 predicted box, anchor box, and ground truth box （y,w,h同理）, $t_i$表示predict box相对于anchor box的偏移，$t_i^{\ast }$表示ground true box相对于anchor box的偏移，学习目标自然就是让前者接近后者的值。

其中 $L_{reg}$ 是：

softmax

三 RPN训练

RPN通过反向传播（BP，back-propagation）和随机梯度下降（SGD，stochastic gradient descent）进行端到端（end-to-end）训练。依照FastR-CNN中的“image-centric”采样策略训练这个网络。每个mini-batch由包含了许多正负样本的单个图像组成。
如果每幅图的所有anchor都去参与优化loss function，那么最终会因为负样本过多导致最终得到的模型对正样本预测准确率很低。因此 在每幅图像中随机采样256个anchors去参与计算一次mini-batch的损失。正负比例1:1(如果正样本少于128则补充采样负样本)

3.1 采样

每一个mini-batch包含从一张图像中随机提取的256个anchor（注意，不是所有的anchor都用来训练），前景样本和背景样本均取128个，达到正负比例为1:1。如果一个图像中的正样本数小于128，则多用一些负样本以满足有256个Proposal可以用于训练。

3.2 初始化

新增的2层参数用均值为0，标准差为0.01的高斯分布来进行初始化，其余层（都是共享的卷积层，与VGG共有的层）参数用ImageNet分类预训练模型来初始化。

3.3 参数化设置（使用caffe实现）

在PASCAL数据集上：

前60k个mini-batch进行迭代，学习率设为0.001；

后20k个mini-batch进行迭代，学习率设为0.0001；

设置动量momentum=0.9，权重衰减weightdecay=0.0005。

3.4 训练

提取proposal的采用RPN，分类采用Fast R-CNN。如何把这两者放在同一个网络结构中训练出一个共享卷积的Multi-task网络模型。如果是分别训练两种不同任务的网络模型，即使它们的结构、参数完全一致，但各自的卷积层内的卷积核也会向着不同的方向改变，导致无法共享网络权重，论文作者提出了三种可能的方式：

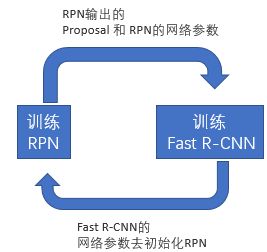
1. Alternating training：此方法其实就是一个不断迭代的训练过程，既然分别训练RPN和Fast-RCNN可能让网络朝不同的方向收敛，a)那么我们可以先独立训练RPN，然后用这个RPN的网络权重对Fast-RCNN网络进行初始化并且用之前RPN输出proposal作为此时Fast-RCNN的输入训练Fast R-CNN。b) 用Fast R-CNN的网络参数去初始化RPN。之后不断迭代这个过程，即循环训练RPN、Fast-RCNN

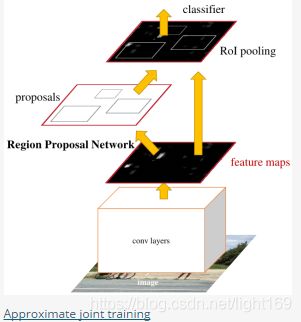
2. Approximate joint training：这里与前一种方法不同，不再是串行训练RPN和Fast-RCNN，而是尝试把二者融入到一个网络内，具体融合的网络结构如下图所示，可以看到，proposals是由中间的RPN层输出的，而不是从网络外部得到。需要注意的一点，名字中的"approximate"是因为反向传播阶段RPN产生的cls score能够获得梯度用以更新参数，但是proposal的坐标预测则直接把梯度舍弃了，这个设置可以使backward时该网络层能得到一个解析解（closed results），并且相对于Alternating traing减少了25-50%的训练时间。(此处不太理解： 每次mini-batch的RPN输出的proposal box坐标信息固定，让Fast R-CNN的regressor去修正位置？)
   

3. Non-approximate training：上面的Approximate joint training把proposal的坐标预测梯度直接舍弃，所以被称作approximate，那么理论上如果不舍弃是不是能更好的提升RPN部分网络的性能呢？作者把这种训练方式称为“ Non-approximate joint training”，但是此方法在paper中只是一笔带过，表示“This is a nontrivial problem and a solution can be given by an “RoI warping” layer as developed in [15], which is beyond the scope of this paper”，

作者发布的源代码里却用了另外一种叫做4-Step Alternating Training的方法，思路和迭代的Alternating training有点类似，但是细节有点差别：

第一步：用ImageNet模型初始化，独立训练一个RPN网络；
第二步：仍然用ImageNet模型初始化，但是使用上一步RPN网络产生的proposal作为输入，训练一个Fast-RCNN网络，至此，两个网络每一层的参数完全不共享；
第三步：使用第二步的Fast-RCNN网络参数初始化一个新的RPN网络，但是把RPN、Fast-RCNN共享的那些卷积层的learning
rate设置为0，也就是不更新，仅仅更新RPN特有的那些网络层，重新训练，此时，两个网络已经共享了所有公共的卷积层；
第四步：仍然固定共享的那些网络层，把Fast-RCNN特有的网络层也加入进来，形成一个unified network，继续训练，fine
tune Fast-RCNN特有的网络层，此时，该网络已经实现我们设想的目标，即网络内部预测proposal并实现检测的功能。

四 参考

[1]: Faster RCNN 学习笔记
[2]: Faster R-CNN理解、讨论
[3]: Faster R-CNN论文笔记——FR
[4]: