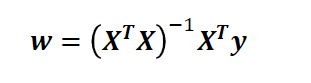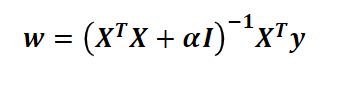机器学习应用——监督学习（上）（实例:人体运动状态预测&人体运动状态预测&房价与房屋尺寸关系的线性拟合与非线性拟合&交通流量预测）

前言

机器学习应用博客中，将核心介绍三大类学习，即：无监督学习、监督学习、强化学习。

本篇将简要介绍：
1.监督学习概念（最常应用场景：分类和回归）
2.分类——k近邻分类器、决策树、朴素贝叶斯（人体运动状态预测）、SVM（人体运动状态预测）
3.回归——线性回归（Linear Regression）（房价与房屋尺寸关系的线性拟合）；多项式回归（Polynomial Regression）（房价与房屋尺寸的非线性拟合）；岭回归(ridge regression）（交通流量预测）

一、监督学习

1.监督学习的目标

①利用一组带有标签的数据，学习从输入到输出的映射，然后将这种映射关系应用到未知数据上，达到分类或回归的目的
②分类：当输出是离散的，学习任务为分类任务
③回归：当输出是连续的，学习任务为回归任务

2.分类学习

（1）输入输出
①输入：一组有标签的训练数据（也称观察和评估），标签表明了这些数据（观察）的所属类别
②输出:分类模型根据这些训练数据,训练自己的模型参数,学习出一个适合这组数据的分类器,当有新数据(非训练数据)需要进行类别判断，就可以将这组新数据作为输人送给学好的分类器进行判断。

（2）分类学习–评价
1）训练集（training set）：顾名思义用来训练模型的已标注数据，用来建立模型，发现规律
2）测试集（testing set）：也是已标注数据，通常做法是将标注隐藏，输送给训练好的模型，通过结果与真实标注进行对比，评估模型的学习能力
3）训练集/测试集的划分方法:根据已有标注数据,随机选出一部分(70%）数据作为训练数据,余下的作为测试数据,此外还有交叉验证法,自助法用来评估分类模型。

（3）分类学习–评价标准

1）精确率:精确率是针对我们预测结果而言的,(以二分类为例）它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了，一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP)。
P = TP/(TP+FP)

2）召回率:是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能，一种是把原来的正类预测成正类（TP)，另一种就是把原来的正类预测为负类（FN）。
R = TP/(TP+FN)

（4）举例
①我们手上有60个正样本,40个负样本,我们要找出所有的正样本,分类算法查找出50个,其中只有40个是真正的正样本
②TP:将正类预测为正类数40;FN:将正类预测为负类数20;FP:将负类预测为正类数10;TN:将负类预测为负类数30。
③准确率(accuracy)=预测对的/所有 = (TP+TN)/(TP+TN+FN+FP) = 70%

（5）Sklearn vs. 分类
①与聚类算法被统一封装在sklearn.cluster模块不同,sklearn库中的分类算法并未被统一封装在一个子模块中，因此对分类算法的import方式各有不同。

②sklearn提供的分类函数
1）k近邻（knn）
2）朴素贝叶斯（naivebayes）
3）支持向量机（svm）
4）决策树（decision tree）
5）神经网络模型（Neural networks）
其中有线性分类器，也有非线性分类器

（6）分类算法的应用
①金融:贷款是否批准进行评估
②医疗诊断:判断一个肿瘤是恶性还是良性
③欺诈检测:判断一笔银行的交易是否涉嫌欺诈
④网页分类:判断网页的所属类别，财经或者是娱乐?

3.回归分析

（1）定义
①回归：统计学分析数据的方法,目的在于了解两个或多个变数间是否相关、研究其相关方向与强度,并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。

②回归分析可以帮助人们了解在自变量变化时因变量的变化量。一般来说,通过回归分析我们可以由给出的自变量估计因变量的条件期望。

（2）Sklearn vs. 回归

①Sklearn提供的回归函数主要被封装在两个子模块中,分别是sklearn.linear_model和sklearn.preprocessing。sklearn.linear_modlel封装的是一些线性函数。

②线性回归函数
1）普通线性回归函数（LinearRegression）
2）岭回归（Ridge）
3）Lasso（Lasso）

③非线性回归函数：多项式回归则通过调用sklearn.preprocessing子模块进行拟合。

（3）回归应用
①回归方法适合对一些带有时序信息的数据进行预测或者趋势拟合,常用在金融及其他涉及时间序列分析的领域。
②股票趋势预测
③交通流量预测

二、分类

1.人体运动状态预测–实例分析

（1）背景介绍
①可穿戴式设备的流行,让我们可以更便利地使用传感器获取人体的各项数据,甚至生理数据。
②当传感器采集到大量数据后,我们就可以通过对数据进行分析和建模,通过各项特征的数值进行用户状态的判断，根据用户所处的状态提供给用户更加精准、便利的服务。

（2）数据介绍
①我们现在收集了来自A,B,C,D,E5位用户的可穿戴设备上的传感器数据,每位用户的数据集包含一个特征文件(a.feature）和一个标签文件(a.label)。
②特征文件中每一行对应一个时刻的所有传感器数值,标签文件中每行记录了和特征文件中对应时刻的标记过的用户姿态,两个文件的行数相同,相同行之间互相对应。

（3）数据构成
①特征文件共包含41列特征,数据内容如下图。

②数据文件的各项特征
1）第一列：记录的时间戳
2）第二列：用户心率
3）3-15、16-28、29-41列：分别为3个姿态传感器的数据
4）文件中的问号代表缺失值

③传感器1的数据特征

1项温度数据、3项一型三轴加速度数据、3项二型三轴加速度数据、3面三轴陀螺仪数据和3项三轴磁场数据。

（4）数据详解
①人体的温度数据可以反映当前活动的剧烈程度,一般在静止状态时,体温趋于稳定在36.5度上下;当温度高于37度时,可能是进行短时间的剧烈运动，比如跑步和骑行。

②在数据中有两个型号的加速度传感器,可以通过互相印证的方式,保证数据的完整性和准确性。通过加速度传感器对应的三个数值,可以知道空间中x、y、z三个轴上对应的加速度,而空间上的加速度和用户的姿态有密切的关系，比如用户向上起跳时,z轴上的加速度会激增。

③陀螺仪是角运动检测的常用仪器,可以判断出用户佩戴传感器时的身体角度是水平、倾斜还是垂直。直观地,通过这些数值都是推断姿态的重要指标。

④磁场传感器可以检测用户周围的磁场强度和数值大小,这些数据可以帮助我们理解用户所处的环境。比如在一个办公场所,用户座位附近的磁场是大体上固定的,当磁场发生改变时,我们可以推断用户的位置和场景发生了变化。

（5）标签文件的介绍
①标签文件内容如图所示,每一行代表与特征文件中对应行的用户姿态类别。总共有0-24共25种身体姿态,如,无活动状态,坐态、跑态等。
②标签文件作为训练集的标准参考准则,可以进行特征的监督学习。

（6）任务介绍
①假设现在出现了一个新用户,但我们只有传感器采集的数据,那么该如何得到这个新用户的姿态呢?
②又或者对同一用户如果传感器采集了新的数据,怎么样根据新的数据判断当前用户处于什么样的姿态呢?
③在明确这是一个分类问题的情况下,我们可以选定某种分类模型(或者说是算法），通过使用训练数据进行模型学习,然后对每个测试样本给出对应的分类结果。

（7）机器学习的分类算法众多,在接下来的学习中我们将会详细介绍经典的分类算法,如K近邻、决策树和朴素贝叶斯的原理和实现。

2.基本分类模型——k近邻分类器

（1）k近邻分类器
①KNN:通过计算待分类数据点,与已有数据集中的所有数据点的距离。取距离最小的前K个点,根据“少数服从多数”的原则,将这个数据点划分为出现次数最多的那个类别。
②sklearn中的K近邻分类器：在sklearn库中，可使用sklearn.neighbors.KNeighborsClassifier创建一个K近邻分类器

主要参数：
1）n_neighbbors：用于指定分类器中K的大小（默认值Wie5，注意与kmeans的区别）
2）weights：设置选中的K个点对分类结果影响的权重（默认值为平均权重“uniform"，可以选择distance代表越近的点权重越高，或者传入自己编写的以距离为参数的权重计算函数）

3）algorithm:设置用于计算临近点的方法,因为当数据量很大的情况下计算当前点和所有点的距离再选出最近的k各点，这个计算量是很费时的，所以选项中有ball_tree、kd_tree和brute,分别代表不同的寻找邻居的优化算法，默认值为auto，根据训练数据自动选择。

（2）K近邻分类器的使用

①创建一组数据X和它对应的标签y
X = [[0],[1],[2],[3]]
y = [0,0,1,1]

②使用import语句导入K近邻分类器
from sklearn.neighbors import KNeighborsClassifier

③参数n neighbors设置为3,即使用最近的3个邻居作为分类的依据,其他参数保持默认值,并将创建好的实例赋给变量neigh。
neigh = KNeighborsClassifier(n_neighbors=3)

④调用fit（）函数，将训练数据X和标签y送入分类器进行学习
neigh.fix(X,y)

⑤调用predict(函数,对未知分类样本[1.1]分类,可以直接并将需要分类的数据构造为数组形式作为参数传入，得到分类标签作为返回值。
print(neigh.predict([[1,1]]))

⑥样例输出值是0,表示K近邻分类器通过计算样本[1.1]与训练数据的距离,取0,1,2这3个邻居作为依据,根据“投票法”最终将样本分为类别0。

from sklearn.neighbors import KNeighborsClassifier
X = [[0],[1],[2],[3]]
y = [0,0,1,1]
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X,y)
print(neigh.predict([[1.1]]))

（3）KNN的使用经验
①在实际使用时,我们可以使用所有训练数据构成特征X和标签y，使用fit(函数进行训练。
②在正式分类时,通过—次性构造测试集或者一个一个输人样本的方式,得到样本对应的分类结果。
③有关K的取值:
1）如果较大,相当于使用较大邻域中的训练实例进行预测,可以减小估计误差,但是距离较远的样本也会对预测起作用,导致预测错误。
2）相反地,如果K较小,相当于使用较小的邻域进行预测,如果邻居恰好是噪声点,会导致过拟合。
3）—般情况下,K会倾向选取较小的值,并使用交叉验证法选取最优K值。

3.基本分类模型——决策树

（1）决策树
①决策树是一种树形结构的分类器,通过顺序询问分类点的属性决定分类点最终的类别。
②通常根据特征的信息增益或其他指标,构建一颗决策树。
③在分类时,只需要按照决策树中的结点依次进行判断,即可得到样本所属类别。
④举例：例如，根据下图这个构造好的分类决策树，一个无房产,单身,年收入55K的人的会被归人无法偿还信用卡这个类

（2）sklearn中的决策树
①在sklearn库中，可使用sklearn.tree.DecisionTreeClassifier创建一个决策树用于分类
②主要参数
1）criterion：用于选择属性的准则，可传入“gini”代表基尼系数，或者entropy代表信息增益
2）max_features：表示在决策树结点进行分裂时，从多少个特征中选择最优特征。可以设定固定数目、百分比或其他标准。它的默认值是使用所有特征个数。

（3）决策树的使用
①决策树本质上是寻找一种对特征空间上的划分,旨在构建一个训练数据拟合的好,并且复杂度小的决策树。
②实际使用中,需要根据数据情况,调整DecisionTreeClassifier类中传入的参数,比如选择合适的criterion,设置随机变量等。

# 导入sklearn内嵌的鸢尾花数据集
from sklearn.datasets import load_iris

# 使用import语句导入决策树分类器,同时导入计算交叉验证值的函数cross_val score
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score

# 使用默认参数,创建一颗基于基尼系数的决策树，并将该决策树分类器赋值给变量clf
clf = DecisionTreeClassifier()

# 将鸢尾花数据赋值给变量iris
iris = load_iris()

# 将决策树分类器做为待评估的模型，iris.data鸢尾花数据做为特征，iris.target鸢尾 花分类标签做为目标结果，通过设定cv为10，使用10折交叉验证。得到最终的交叉验证得分
cross_val_score(clf,iris.data,iris.target,cv=10)

# 可以仿照之前K近邻分类器的使用方法,利用fit()函数训练模型并使用predict()函数预测
# clf.fit(X,y)
# clf.predict(x)

4.基本分类模型——朴素贝叶斯

（1）朴素贝叶斯
①朴素贝叶斯分类器是一个以贝叶斯定理为基础的多分类的分类器。
②对于给定数据,首先基于特征的条件独立性假设,学习输入输出的联合概率分布,然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。

（2）sklearn中的朴素贝叶斯
①在sklearn库中,实现了三个朴素贝叶斯分类器

②区别在于假设某一特征的所有属于某个类别的观测值符合特定分布
③如分类问题的特征包括人的身高,身高符合高斯分布,则这类问题适合高斯朴素贝叶斯
④在sklearn库中，可使用sklearn.naive.bayes.GaussianNB创建一个高斯朴素贝叶斯分类器
⑤参数
priors:给定各个类别的先验概率。如果为空，则按训练数据的实际情况进行统计;如果给定先验概率,则在训练过程中不能更改。

（3）朴素贝叶斯的使用

①朴素贝叶斯是典型的生成学习方法,由训练数据学习联合概率分布,并求得后验概率分布。
②朴素贝叶斯一般在小规模数据上的表现很好,适合进行多分类任务。

# 导入numpy库，并构造训练数据X和y
import numpy as np
X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
Y = np.array([1,1,1,2,2,2])

# 使用import语句导入朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB

# 使用默认参数,创建一个高斯朴素贝叶斯分类器,并将该分类器赋给变量clf
clf = GaussianNB(priors=None)

# 类似的,使用fit(函数进行训练,并使用predict(函数进行预测,得到预测结果为1。（测试时可以构造二维数组达到同时预测多个样本的目的)
clf.fit(X,Y)
print(clf.predict([[-0.8,-1]]))

5.人体运动状态预测——程序编写

（1）算法流程
①需要从特征文件和标签文件中将所有数据加载到内存中,由于存在缺失值,此步骤还需要进行简单的数据预处理。
②创建对应的分类器,并使用训练数据进行训练。
③利用测试集预测,通过使用真实值和预测值的比对,计算模型整体的准确率和召回率,来评测模型。

（2）代码实现
①模块导入
②数据导入函数
③主函数——数据准备
④主函数——knn
⑤主函数——决策树
⑥主函数——贝叶斯
⑦主函数——分类结果分析

# 模块导入
# 导入numpy库和pandas库
import numpy as np
import pandas as pd

# 从sklearn库中导入预处理模块Imputer
from sklearn.impute import SimpleImputer #新版本0.20以来 SimpleImputer 代替 Imputer,故代码有所变动

# 导入自动生成训练集和测试集的模块train_test_split
from sklearn.model_selection import train_test_split

# 导入预测结果评估模块classification_report
from sklearn.metrics import classification_report

# 依次导入3个分类器模块
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import GaussianNB

# 数据导入函数
def load_dataset(feature_paths, label_paths): # 传入两个参数：特征文件的列表和标签文件的列表
    feature = np.ndarray(shape=(0,41)) #列数量和特征维度一致为41;
    label = np.ndarray(shape=(0,1)) # 义空的标签变量,列数量与标签维度一致为1

    for file in feature_paths:
        df = pd.read_table(file,delimiter=',',na_values='?',header=None)# 用逗号分隔符读取特征数据，问号替换标记为缺失值，文件中不包含表头
        imp = SimpleImputer(missing_values="NaN",strategy='mean',verbose=0) #使用平均值不全缺失值，将数据补全
        imp.fit(df) #训练预处理器
        df = imp.transform(df) #生成预处理结果
        feature = np.concatenate((feature,df)) # 将新读入的数据合并到特征集中，依次遍历完所有特征文件

    for file in label_paths:
        df = pd.read_table(file,header=None) # 读取文件数据，不含表头
        label = np.concatenate((label,df)) # 由于标签文件没有缺失值,所以直接将读取到的新数据加入label集合,依次遍历完所有标签文件,得到标签集label.
    label = np.ravel(label) # 将标签规整为一维向量
    return feature,label # 读取内容，归并后返回

# 主函数——数据准备
if __name__ == '__main__':
    # 设置数据路径
    featurePaths = ['A/A.feature', 'B/B.feature', 'C/C.feature', 'D/D.feature', 'E/E.feature']
    labelPaths = ['A/A.label', 'B/B.label', 'C/C.label', 'D/D.label', 'E/E.label']
    # 使用python的分片方法，将数据路径中的前4个值作为训练集，并作为参数传入load_dataset()函数中，得到训练集合的特征x_train，训练集的标签y_train。
    x_train,y_train = load_dataset(featurePaths[:4],labelPaths[:4])
    # 将最后一个值对应的数据作为测试集, 送入load_dataset(函数中, 得到测试集合的特征x_test，测试集的标签y_test。
    x_test,y_test = load_dataset(featurePaths[:4], labelPaths[:4])
    # 使用全量数据作为训练集，借助train_test_split函数将训练数据打乱
    x_train,x_,y_train,y_ = train_test_split(x_train,y_train,train_size=0.0)

    # 主函数——knn
    print("Start training knn")
    knn = KNeighborsClassifier().fit(x_train,y_train) #使用默认参数创建k近邻分类器，并将训练集x_train和y_train送入fit()函数进行训练，训练后的分类器保存到变量knn中。
    print("Training done!")
    answer_knn = knn.predict(x_test)
    print("Prediction done!") #使用测试集x_test，进行分类器预测，得到分类结果answer_knn。

    # 主函数——决策树
    print("Start training DT")
    dt = DecisionTreeClassifier().fit(x_train,y_train) #使用默认参数创建决策树分类器dt，并将训练集x_train和y_train送入fit()函数进行训练。训练后的分类器保存到变量dt中。
    print("Training done!")
    answer_dt = dt.predict(x_test) #使用测试集x_test，进行分类器预测，得到分类结果answer_dt。
    print("Prediction done!")

    #主函数——贝叶斯
    print('Start training Bayes')
    gnb = GaussianNB().fit(x_train, y_train) #使用默认参数创建贝叶斯分类器，并将训练集x_train和y_train送入fit()函数进行训练。训练后的分类器保存到变量gnb中。
    print('Training done')
    answer_gnb = gnb.predict(x_test) #使用测试集x_test，进行分类器预测，得到分类结果answer_gnb。
    print('Prediction done')

    # 主函数——分类结果分析
    # 使用classification_report函数对分类结果，从精确率precision、召回率recall、f1值f1-scor和支持度support四个维度进行衡量。
    #  分别对三个分类器的分类结果进行输出
    print("\n\nThe classification report for knn:")
    print(classification_report(y_test,answer_knn))

    print("\n\nThe classification report for dt:")
    print(classification_report(y_test, answer_dt))

    print("\n\nThe classification report for gnb:")
    print(classification_report(y_test, answer_gnb))

（3）结果展示
①K近邻

②决策树

③贝叶斯

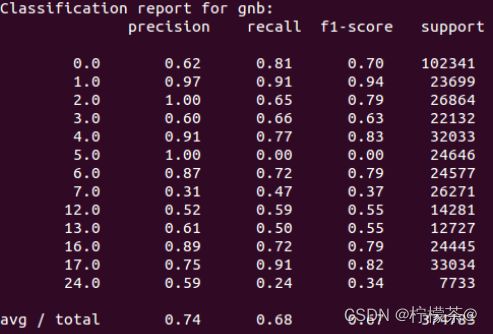
（4）结果对比

（5）结论
①从准确度的角度衡量,贝叶斯分类器的效果最好
②从召回率和F1值的角度衡量,k近邻效果最好
③贝叶斯分类器和k近邻的效果好于决策树

（6）思考
①在所有的特征数据中,可能存在缺失值或者冗余特征。如果将这些特征不加处理地送入后续的计算,可能会导致模型准确度下降并且增大计算量。
②特征选择阶段,通常需要借助辅助软件(例如Weka)将数据进行可视化并进行统计。
③思考如何筛选冗余特征,提高模型训练效率,也可以尝试调用sklearn提供的其他分类器进行数据预测。

6.上证指数涨跌预测实例

（1）数据介绍：网易财经上获得的上证指数的历史数据,爬取了150天的上证指数数据。
（2）实验目的:根据给出当前时间前150天的历史数据,预测当天上证指数的涨跌。
（3）技术路线：sklearn.SVC
（4）中核科技1990年到2017年的股票数据部分截图,红框部分为选取的特征值。

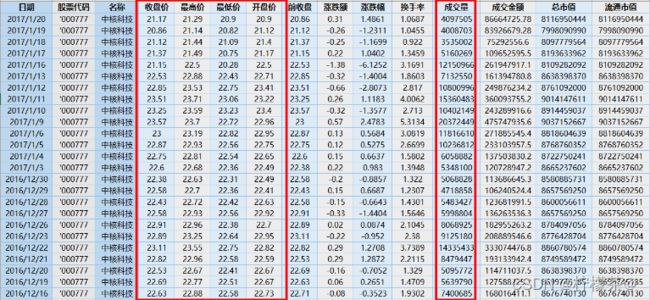
（5）使用算法（SVM）
①建立过程，导入sklearn相关包
②数据加载&&数据预处理

③创建SVM并进行交叉验证

# 建立过程，导入sklearn相关包
import pandas as pd
import numpy as np
from sklearn import svm
from sklearn import model_selection

# 数据加载&&数据预处理
data = pd.read_csv('stock/000777.csv',encoding='gbk',parse_dates=[0],index_col=0) #pandas.read_csv(数据源, encoding=编码格式为gbk,parse_dates=第O列解析为日期，index_col=用作行索引的列编号)
data.sort_index(0,ascending=True,inplace=True) # DataFrame.sort_index(axis=0(按0列排), ascending=True (升序) , inplace=False(排序后是否覆盖原序列）
#选取5列数据作为特征:收盘价、最高价、最低价、开盘价、成交量
# data.shape[0]-dayfeature意思是因为我们要用150天数据做训练，对于条目为200条的数据，只有50条数据是有前150天的数据来训练的,所以训练集的大小就是200-150，对于每一条数据，他的特征是前150天的所有特征数据,即150*5，+1是将当天的开盘价引入作为一条特征数据。
dayfeature = 150#选150天的数据
featurenum = 5*dayfeature #选取的5个特征*天数
x = np.zeros((data.shape[0]-dayfeature,featurenum+1)) #记录150天的5个特征值
y = np.zeros((data.shape[0]-dayfeature)) #记录涨或者跌

for i in range(0,data.shape[0]-dayfeature):
    x[i,0:featurenum] = np.array(data[i:i+dayfeature]\
        [[u'收盘价',u'最高价',u'最低价',u'开盘价',u'成交量']]).reshape(1,featurenum)# 将5个数据特征存入数组中
    x[i,featurenum] = data.ix[i+dayfeature][u'开盘价'] #最后一列记录当日开盘价

for i in range(0,data.shape[0]-dayfeature):
    if data.ix[i+dayfeature][u'收盘价']>=data.ix[i+dayfeature][u'开盘价']:
        y[i] = 1
    else:
        y[i] = 0 #如果当天收盘价高于开盘价，y[i]=1代表涨，O代表跌

# 创建SVM并进行交叉验证
clf = svm.SVC(kernel='rbf') #调用SVM函数，并设置kermel参数，默认是rbf，其他:"linear”"poly""sigmoid"
result = []
for i in range(5):
    x_train,x_test,y_train,y_test = model_selection.train_test_split(x,y,test_size=0.2) #x和y的验证集合测试集，切分80-20%的测试集
    clf.fit(x_train,y_train) #训练数据
    result.append(np.mean(y_test==clf.predict(x_test)))#将预测数据和测试集的数据比对
print("svm classfier accuracy:")
print(result)

（6）实验结果

本次实验运用了两个核函数做实验,准确率由表中数据所示。5次交叉验证的准确率相近,均为53%左右。

（7）交叉验证
①基本思想:交叉验证法先将数据集D划分为k个大小相似的互斥子集,每个子集都尽可能保持数据分布的一致性,即从D中通过分层采样得到。
②每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集;这样就可获得k组训练/测试集,从而可进行k次训练和测试,
③最终返回的是这个k个测试结果的均值。通常把交叉验证法称为“k者交叉验证”
④k最常用的取值是10,此时称为10折交叉验证。

三、回归

1.线性回归（Linear Regression）

（1）介绍
①利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法
②利用称为“线性回归方程的最小平方函数”对一个或多个自变量和因变量之间关系进行建模，这种函数是一个或多个回归系数的模型参数的线性组合

（2）分类
①简单回归：只有一个自变量的情况
②多元回归：大于一个自变量情况

（3）定义
使用形如y = w^t*x+b的线性模型拟合数据输入和输出之间映射关系

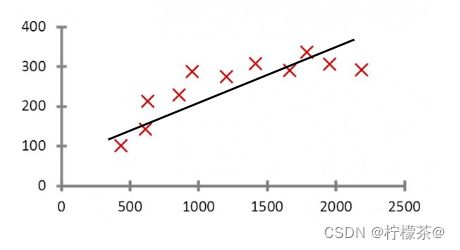
（4）用途
①如果目标是预测或者映射,线性回归可以用来对观测数据集的y和X的值拟合出一个预测模型。当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。
②给定一个变量y和一些变量X1,…,Xp,这些变量有可能与y相关,线性回归分析可以用来量化y与X之间相关性的强度,评估出与y不相关的X，并识别出哪些X的子集包含了关于y的冗余信息。

2.房价与房屋尺寸关系的线性拟合（线性回归的应用）

（1）背景
①与房价密切相关的除了单位的房价,还有房屋的尺寸。
②我们可以根据已知的房屋成交价和房屋的尺寸进行线性回归,继而可以对已知房屋尺寸,而未知房屋成交价格的实例进行成交价格的预测。
③目标：对房屋成交信息建立回归方程,并依据回归方程对房屋价格进行预测。

（2）技术路线：sklearn.linear_model.LinearRegression

（3）实例数据
①为了方便展示,成交信息只使用了房屋的面积以及对应的成交价格。
②房屋面积单位为平方英尺(f*t^2)
③房屋成交价格单位为万元

（4）可行性分析
①简单而直观的方式是通过数据的可视化直接观察房屋成交价格与房屋尺寸间是否存在线性关系。
②对于本实验的数据来说,散点图就可以很好的将其在二维平面中进行可视化表示。
③图为数据的散点图,其中横坐标为房屋面积,纵坐标为房屋的成交价格。可以看出,靠近坐标左下角部分的点,表示房屋尺寸较小的房子,其对应的房屋成交价格也相对较低。同样的,靠近坐标右上部分的点对应于大尺寸高价格的房屋。从总体来看,房屋的面积和成交价格基本成正比。

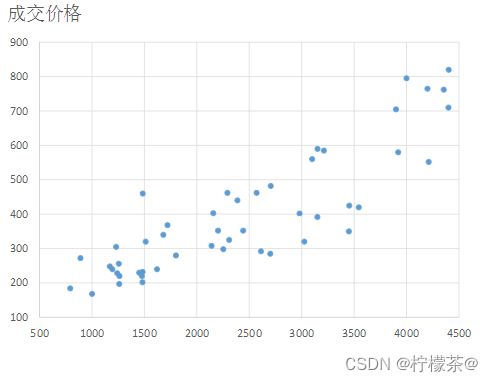
（5）代码实现
①使用算法：线性回归
②实现步骤
1）建立工程并导入sklearn包
2）加载训练数据，建立回归方程
3）可视化处理

③调用sklearn.linear_model.LinearRegression()所需参数
1）fit_intercept：布尔型参数，表示是否计算该模型截距，可选参数
2）normalize：布尔型参数，若为True，则X在回归前进行归一化，可选参数，默认值False
3）copy_X：布尔型参数，若为True，则X将被复制，否则将被覆盖，可选参数，默认值为True
4）n_jobs：整型参数，表示用于计算的作业数量，若为-1，则用所有的CPU，可选参数，默认值1

④线性回归fit函数用于拟合输入输出数据，调用形式为linear.fit(x,y，sample_weight=None):
1）X：X为训练向量﹔
2）y：y为相对于X的目标向量;
3）sample weight：分配给各个样本的权重数组，一般不需要使用，可省略。

⑤如果有需要，可以通过两个属性查看回归方程的系数及截距。
1）查看回归方程系数
print(‘Coefficients:’,linear.coef_)
2）查看回归方程截距
print(‘intercept:’,linear.intercept)

# 建立工程并导入sklearn包
import matplotlib.pyplot as plt #matplotlib的pyplot子库，它提供了和matlab类似的绘图API。
import numpy as np
from sklearn import linear_model #可以调用sklearn中的linear_model模块进行线性回归。

# 加载训练数据，建立回归方程
datasets_X = [] # 建立datasets_x和datasets_Y用来存储数据中的房屋尺寸和房屋成交价格。
datasets_Y = []
fr = open('prices.txt','r') # 打开数据集所在文件并读取
lines = fr.readline() # 一次性读取整个文件
for line in lines: # 逐行进行操作，循环遍历所有数据
    items = line.strip().split(',') #取出数据文件中的逗号
    datasets_X.append(int(items[0])) # 将读取的数据转换为int型，并分别写入datasets_X和datasets_Y。
    datasets_Y.append(int(items[1]))
length = len(datasets_X) # 求得datasets_X的长度，即为数据的总数
datasets_X = np.array(datasets_X).reshape([length,1]) #将datasets_x转化为数组，并变为二维，以符合线性回归拟合函数输入参数要求。
datasets_Y = np.array(datasets_Y) # 将datasets_Y转化为数组

minX = min(datasets_X) # 以数据datasets_x的最大值和最小值为范围，建立等差数列，方便后续画图。
maxX = max(datasets_X)
X = np.arange(minX,maxX).reshape([-1,1])

linear = linear_model.LinearRegression() #调用线性回归模块，建立回归方程，拟合数据
linear.fit(datasets_X,datasets_Y)

# 可视化处理
plt.scatter(datasets_X,datasets_Y,color='red') #scatter函数用于绘制数据点，这里表示用红色绘制数据点;
plt.plot(X,linear.predict(X),color='blue') #plot函数用来绘制直线，这里表示用蓝色绘制回归线;
plt.xlabel('Area') #xlabel和ylabel用来指定横纵坐标的名称。
plt.ylabel('Price')
plt.show()

（6）结果展示
通过回归方程拟合的直线与原有数据点的关系如图所示,依据该回归方程即可通过房屋的尺寸,来预测房屋的成交价格。

3.多项式回归（Polynomial Regression）

（1）介绍
①研究一个因变量或多个自变量间多项式的回归分析方法
②在一元回归分析中,如果依变量y与自变量X的关系为非线性的,但是又找不到适当的函数曲线来拟合,则可以采用一元多项式回归。
③多项式回归的最大优点就是可以通过增加X的高次项对实测点进行逼近,直至满意为止。
④事实上,多项式回归可以处理相当一类非线性问题,它在回归分析中占有重要的地位,因为任一函数都可以分段用多项式来逼近。

（2）分类
①一元多项式回归：自变量仅1个
②多元多项式回归：自变量多个

（3）方程
①一元m次多项式回归方程

   ②二元二次多项式回归方程

（4）区别
①线性回归实例中,是运用直线来拟合数据输入与输出之间的线性关系。
②不同于线性回归,多项式回归是使用曲线拟合数据的输入与输出的映射关系。

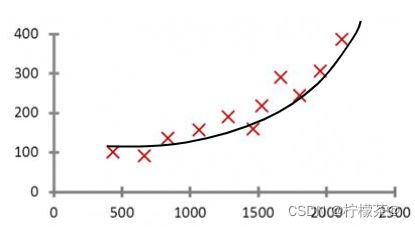
4.多项式回归应用（房价与房屋尺寸的非线性拟合）

（1）背景
①根据已知的房屋成交价和房屋的尺寸进行了线性回归,继而可以对已知房屋尺寸，而未知房屋成交价格的实例进行了成交价格的预测
②但是在实际的应用中这样的拟合往往不够好,因此我们在此对该数据集进行多项式回归。
③目标：对房屋成交信息建立多项式回归方程,并依据回归方程对房屋价格进行预测。

（2）技术路线：sklearn.preprocessing.PolynomialFeatures
（3）实例数据：同上

（4）代码实现（线性回归）
①实现步骤
1）建立工程并导入sklearn包
2）加载训练数据，建立回归方程
3）可视化处理
②sklearn中多项式回归
1）这里的多项式回归实际上是先将变量X处理成多项式特征，然后使用线性模型学习多项式特征的参数,以达到多项式回归的目的。
2）例如：X = [x1,x2]
使用PolynomialFeatures构造X的二次多项式特征X_Poly

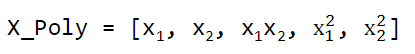
使用linear model学习X_Poly和y之间的映射关系,即参数

# 建立工程并导入sklearn包
import matplotlib.pyplot as plt #matplotlib的pyplot子库，它提供了和matlab类似的绘图API。
import numpy as np
from sklearn import linear_model #可以调用sklearn中的linear_model模块进行线性回归。
from sklearn.preprocessing import PolynomialFeatures #导入线性模型和多项式特征构造模块

# 加载训练数据，建立回归方程
datasets_X = [] # 建立datasets_x和datasets_Y用来存储数据中的房屋尺寸和房屋成交价格。
datasets_Y = []
fr = open('prices.txt','r') # 打开数据集所在文件并读取
lines = fr.readline() # 一次性读取整个文件
for line in lines: # 逐行进行操作，循环遍历所有数据
    items = line.strip().split(',') #取出数据文件中的逗号
    datasets_X.append(int(items[0])) # 将读取的数据转换为int型，并分别写入datasets_X和datasets_Y。
    datasets_Y.append(int(items[1]))
length = len(datasets_X) # 求得datasets_X的长度，即为数据的总数
datasets_X = np.array(datasets_X).reshape([length,1]) #将datasets_x转化为数组，并变为二维，以符合线性回归拟合函数输入参数要求。
datasets_Y = np.array(datasets_Y) # 将datasets_Y转化为数组

minX = min(datasets_X) # 以数据datasets_x的最大值和最小值为范围，建立等差数列，方便后续画图。
maxX = max(datasets_X)
X = np.arange(minX,maxX).reshape([-1,1])

poly_reg = PolynomialFeatures(degree=2) #degree=2表示建立datasets_X的二次多项式特征X_poly
X_poly = poly_reg.fit_transform(datasets_X)
lin_reg_2 = linear_model.LinearRegression()
lin_reg_2.fit(X_poly,datasets_Y) #然后创建线性回归，使用线性模型学习x_poly和datasets_Y之间的映射关系（即参数)。

# 可视化处理
plt.scatter(datasets_X,datasets_Y,color='red') #scatter函数用于绘制数据点，这里表示用红色绘制数据点;
plt.plot(X,lin_reg_2.predict(poly_reg.fit_transform(X)),color='blue') #plot函数用来绘制直线，这里需要先将X处理成多项式特征
plt.xlabel('Area') #xlabel和ylabel用来指定横纵坐标的名称。
plt.ylabel('Price')
plt.show()

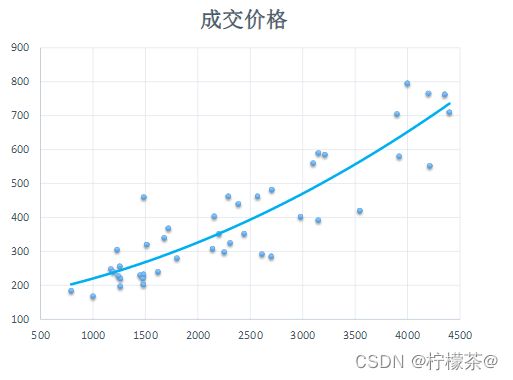
（5）结果展示
①通过多项式回归拟合的曲线与数据点的关系如图所示。
②依据该多项式回归方程即可通过房屋的尺寸,来预测房屋的成交价格。

5.岭回归

（1）线性回归弊端
①对于一般地线性回归问题,参数的求解采用的是最小二乘法，其目标函数如下:

②参数w的求解,也可以使用如下矩阵方法进行:

观察此解可得：
1）对于矩阵X,若某些列线性相关性较大（即训练样本中某些属性线性相关),就会导致X^T*X的值接近0,在计算其逆时就会出现不稳定性。
2）对应于训练样本即为，一个样本点的小幅度变化，导致求得的参数w发生很大变化
③结论:传统的基于最小二乘的线性回归法缺乏稳定性。为此引出岭回归

（2）岭回归
①岭回归(ridge regression）是一种专用于共线性数据分析的有偏估计回归方法。
②优化目标（在平方误差的基础上增加正则项）

③对应的矩阵求解方法为

其中，α为正数，I对应单位阵，可保证不发生巨大跳变，保证w的稳定性
④是一种改良的最小二乘估计法,对某些数据的拟合要强于最小二乘法。

（3）sklearn中的岭回归
在sklearn库中，可使用sklearn.linear_model.Ridge调用岭回归模型，主要参数：
①alpha：正则化因子，对应于损失函数中的α
②fit_intercept：表示是否计算截距
③solver：设置计算参数的方法，可选参数’auto’,‘svd’,‘sag’

6.岭回归实例——交通流量预测

（1）数据介绍:数据为某路口的交通流量监测数据,记录全年小时级别的车流量。
（2）实验目的:根据已有的数据创建多项式特征,使用岭回归模型代替一般的线性模型,对车流量的信息进行多项式回归。
（3）技术路线
①sklearn.linear_model.Ridge
②sklearn.preprocessing.PolynomialFeatures

（4）数据实例

（5）数据特征
①HR:一天中的第几个小时(0-23 )
②WEEK_DAY:一周中的第几天（0-6)
③DAY_OF_YEAR;一年中的第几天(1-365)
④WEEK_OF_YEAR:一年中的第几周(1-53)
⑤TRAFFIC COUNT:父通流量
⑥全部数据集包含2万条以上数据（21626)

（6）代码实现
①建立工程,导入sklearn相关工具包
②数据加载

③数据处理
④划分训练集和测试集
⑤创建回归器，并进行训练
注：拟合优度，用于评价拟合好坏，最大为1，无最小值，当对所有输入都输出同一个值时，拟合优度为0。

⑥画出拟合曲线

#建立工程,导入sklearn相关工具包:
import numpy as np
from sklearn.linear_model import Ridge # 加载岭回归方法
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt #加载交叉验证模块，加载matplotilib模块
from sklearn.preprocessing import PolynomialFeatures #通过sklearn.preprocessing加载PolynomialFeatures用于创建多项式特征

# 数据加载
data = np.genfromtxt('data.txt') #使用numpy方法从TXT中加载数据
plt.plot(data[:,4]) #使用ply展示车流量信息

# 数据处理
X = data[:,:4] # 用于保存0-3维数据，即属性
y = data[:,4]# 用于保存第四维数据，即车流量
poly = PolynomialFeatures(6) #用于创建最高次数6次方的多项式特征
X = poly.fit_transform(X) #X为创建的多项式特征

# 划分训练集和测试集
# 将所有数据划分为训练集和测试集，test_size表示测试集的比例，random_state是随机数种子
train_set_X,test_set_X,train_set_y,test_set_y = train_test_split(X,y,test_size=0.3,random_state=0)

# 创建回归器，并进行训练
clf = Ridge(alpha=1.0,fit_intercept=True) #创建岭回归实例
clf.fit(train_set_X,train_set_y) #调用fit函数使用训练集训练回归器
clf.score(train_set_X,train_set_y) #利用测试集计算回归曲线的拟合优度，clf.score返回值为0.7375

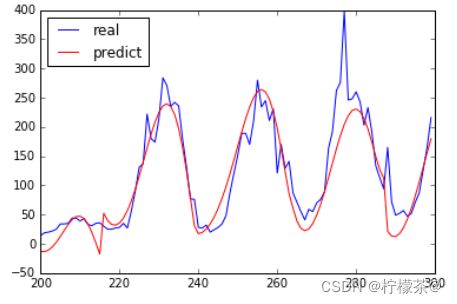
# 画出拟合曲线
start = 200 #画一段200-300范围内的拟合曲线
end = 300
y_pre=clf.predict(X)#是调用predict函数的拟合值
time = np.arange(start,end)
plt.plot(time,y[start:end],'b',label='predict') #展示真实数据（蓝色)以及拟合的曲线（红色)
plt.legend(loc='upper left') #设置图例的位置
plt.show()

⑦结果分析：预测值和实际值的走势大致相同

总结

关于监督学习，比较核心的就是分类和回归问题，在此仅用几个实例说明两大核心的典型方法，其余便不多做赘述。关于代码之中的一些改进问题，由于用到库中的其他方法，且本人能力有限，大家感兴趣可自行查阅官网API。

关于分类，k近邻分类器、决策树、朴素贝叶斯，SVM需熟练掌握
关于回归，比较常用的为线性回归，至于多元非线性拟合及岭回归，根据数据特征不同可适用于不同场所

两点问题：
（1）代码运行需要基础数据支撑，py的自带库中有些内含所需数据，有些则没有，本篇并未放上数据txt文件，只是为了展示无监督学习的体系流程以作演示
（2）在库的包导入若发生问题，看看版本更新问题，以及部分包在近年来命名和函数有所调整，各位客官可面向百度

代码非原创，内容乃课件整理所得。
如有问题，欢迎指正！

下一篇将介绍“手写数字识别”（神经网络实现&KNN实现）
（太长了实在放不下了）