最新综述：用于组合优化的强化学习

©PaperWeekly 原创 · 作者 | 王馨月

学校 | 四川大学本科生

研究方向 | 自然语言处理

摘要

推许多解决组合优化问题的传统算法都涉及使用手工构造的启发式算法，这些启发式算法能够依次地构造解决方案。这种启发式方法是由领域专家设计的，且一般由于问题的困难性，这种方法不是最佳的。强化学习（RL）提出了一种很好的选择，使用监督或自我监督的方式训练 agent 来自动搜索这些启发式方法。

在这篇调研中，我们探索了将 RL 框架应用于困难的组合问题的最新进展。我们的调研为运筹学和机器学习社区提供了必要的背景，并展示了推动领域向前发展的工作。我们将最近提出的 RL 方法并置在一起，列出了每个问题改进方法的时间线，并与传统算法进行了比较，这表明 RL 模型可以成为解决组合问题的有希望的方向。

论文标题：

Reinforcement Learning for Combinatorial Optimization: A Survey

论文作者：

Nina Mazyavkina, Sergey Sviridov, Sergei Ivanov, Evgeny Burnaev

论文链接：

https://arxiv.org/abs/2003.03600

 

引言

优化问题涉及在不同可能中找到优化配置或是“值”，他们天然地属于两个类别中的一个：具有连续变量和离散变量的配置。比如，找到一个凸规划问题的解决方案是一个连续优化问题，而在图的所有路径中找到最短路径则是一个离散优化问题。

有时两者之间的界线很难确定。比如，在连续空间中的线性规划任务可以看作是一个离散的组合问题，因为他的解决方案在凸多边形的顶点的有限集合中，这已经由 Dantzig 的算法证明。通常，离散空间中的优化问题称为组合优化（CO）问题，且与连续空间中的问题相比拥有不同类型的解决方案。可以将 CO 问题表达如下：

定义1：令 是一个元素的集合， 是代价函数。组合优化问题旨在找到函数 的最优值以及在域 上实现该最优值的任何对应的最优元素。

通常，集合 是是有限的，在这种情况下，存在全局最优值。因此，对于任何CO问题，都可以通过比较所有 中的元素 来得到平凡解。注意，定义 1 还包括决策问题的情况，当解决方案是二元（或更普遍的多类）的解决方案时，错误答案的成本比正确答案的成本高。

组合问题的一个常见示例是旅行商问题（TSP）。目标是提供访问每个顶点并返回到初始端点的最短路径，或者换句话说，在全连接的加权图中找到具有最小长度的汉密尔顿回路 。在这种情况下，所有汉密尔顿回路都定义了一组元素，即 所有汉密尔顿路径 ，以及与每个汉密尔顿贿赂相关的成本是回路中边 的权重 的总和 ，即 。

CO 问题的另一个示例是混合整数线性规划（MILP），其目标是对于满足约束 , 的参数 和 ，给定向量 ，最小化 。

许多 CO 问题都是 NP-hard 问题，没有一个有效的多项式时间解。因此，有很多近似或启发式解决这些问题的算法被设计出来。近几年的新兴趋势之一是通过训练机器学习（ML）算法来解决 CO 问题。例如，我们可以在已经解决的 TSP 实例的数据集上训练 ML 算法，以决定对于新 TSP 实例下一步要移动到哪个节点。

我们在本次调研中考虑的 ML 的一个特定分支称为强化学习（RL），对于给定的 CO 问题，它可以定义一个环境并在该环境中起作用的 agent 构造了解决方案。为了将 RL 应用于 CO，将问题建模为顺序决策过程，在此过程中，agent 将通过执行一系列操作来与环境交互以找到解决方案。马尔科夫决策过程（MDP）为建模此类问题提供了广泛使用的数学框架。

定义2：MDP 可以被定义为一个元组 ，其中：

1.  - 状态空间， 。在此调研中，组合优化问题的状态空间通常由以下两种方式之一进行定义。一组方法构造解决方案时，将其逐步定义为问题的部分解决方案集（例如，TSP 问题的部分构造路径）。另一组方法从对问题的次优解决方案开始，然后迭代地加以改善（例如，TSP 的次优方案）；

2.  - 动作空间， 。动作表示对部分解决方案的更改或正在更改的完整解决方案（例如，更改 TSP 路径中的节点顺序）；

3.  - 奖励函数是从状态和动作到实数的映射 。奖励表示在特定状态下选择的动作如何改善或恶化该问题的解决方案（例如，TSP 的行程长度）；

4.  - 过渡函数 响应于动作，控制从一种状态到另一种状态的过渡动力学。在组合优化设置中，过渡动力学通常是确定性的，并且事先已知。

5.  - 标量折扣因子， 。折扣因子鼓励 agent 为短期奖励考虑更多；

6.  - Horizon，它定义了 epoch 的长度，其中 epoch 被定义为序列 。对于逐步构造解决方案的方法，情节的长度自然是由执行的操作数定义的，直到找到解决方案为止。对于迭代方法，引入了一些人工停止标准。

Agent 在 MDP 中行动的目标是找到一个将状态映射为行动的策略函数 。解决 MDP 意味着找到使预期的累积折扣总和最大化的最佳策略：

一旦为 CO 问题定义了 MDP，我们就需要决定 agent 如何搜索最优策略 。广义上讲，有两种 RL 算法：

1. 基于价值的方法：首先计算价值行动函数 ，作为给定状态 ???? 并采取行动 a 的策略 的预期报酬。然后，agent 的策略对应于针对给定状态选择一个最大化 的动作。基于价值的方法之间的主要区别在于如何准确有效地估算 。

2.基于策略的方法：直接将 agent 的策略建模为参数函数 。通过收集 agent 在环境中先前做出的决定（也就是经验），我们可以通过最大化最终奖励 来优化参数 。基于策略的方法之间的主要区别在于用于找到最大化预期的奖励总和的函数 的优化方法。

可以看出，RL 算法取决于将 MDP 状态作为输入并输出动作值或动作的函数。状态代表有关该问题的一些信息，例如给定的图或当前的 TSP 路径，而 Q 值或动作是数字。因此，RL 算法必须包括编码器 encoder，即将状态编码为数字的函数。已经提出了许多针对 CO 问题的编码器，包括递归神经网络 RNN，图神经网络 GNN，基于注意力的网络和多层感知器。 

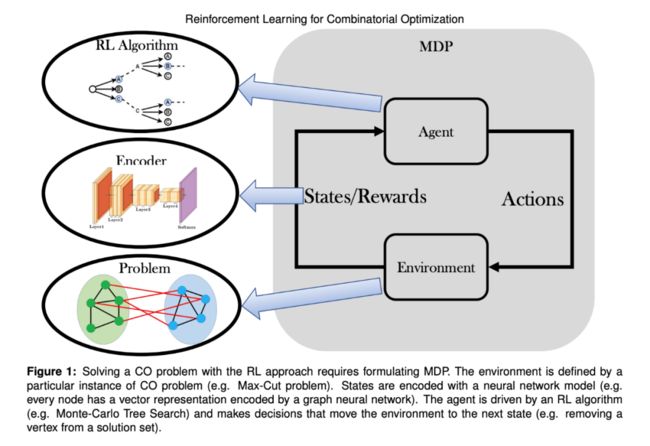
总而言之，图 1 中显示了用于解决 RL 的 CO 问题的 pipeline。首先根据 MDP 重新构造 CO 问题，即我们为给定问题定义状态、动作和奖励。然后我们定义状态的编码器，即对输入状态进行编码并输出数字向量（每个动作的 Q 值或概率）的参数函数。

下一步是实际的 RL 算法，该算法确定 agent 如何学习编码器的参数并为给定的 MDP 做出决策。代理选择动作后，环境移至新状态，并且 agent 会因其执行的动作而获得奖励。然后，该过程从分配的时间预算内的新状态开始重复。训练完模型的参数后，agent 就能针对问题的未知实例搜索解决方案。 

RL 领域技术和方法的最新成功应用激发了我们的工作以解决 CO 问题。尽管原则上可以通过运筹学界中已有相关文献的强化学习算法来解决许多实际的组合优化问题，但我们将专注于针对 CO 问题的 RL 方法。这篇综述涵盖了最新的论文，这些论文展示了如何将强化学习算法应用于重新规划和解决一些规范的优化问题，例如旅行商问题（TSP）、最大割（Max-Cut）问题、最大独立集（MIS） 、最小顶点覆盖（MVC）和装箱问题（BPP）。

总结和进一步的工作

前面的部分介绍了几种通过使用强化学习算法来解决经典组合优化问题的方法。由于该领域已经证明可以与最新的启发式方法和求解器相提并论，因此我们期望在以下可能的方向上出现新的算法和方法，我们认为这是有希望的： 

推广到其他问题：在第五节中，我们提出了 RL-CO 领域当前状态的主要问题之一，即有限的实验比较。确实，数学问题的 CO 组非常庞大，并且当前的方法通常需要针对一组具体的问题实施。但是，RL 领域已经采取了一些措施，将学习到的策略推广到未解决的问题。对于 CO，这些看不见的问题可能是同一问题的较小实例、分布不同的问题实例、甚至是另一组 CO 问题中的问题实例。我们相信，尽管这个方向充满挑战，但它对于 RL-CO 领域的未来发展是极有希望的。 

提高解决方案质量：与商业解决方案相比，本调研中展示的许多先前的工作都表现出卓越的性能。而且，它们中的一些还已经达到了与最优解或通过启发式算法实现的解相等的质量。但是，这些结果仅适用于复杂度较低的 CO 问题，例如节点数量较少的问题。这给我们留下了在客观质量方面进一步改进当前算法的可能性。某些可行的方法可能是将经典 CO 算法与 RL 方法进一步结合，例如，使用模仿学习。 

填补 gap：我们前面已经提到过，对 RL-CO 方法进行分类的方法之一是将它们分为联合方法和构造方法。表 1、2、3、4、5 包含有关每篇评论文章的这些标签的信息，从中，我们可以为每种 CO 问题确定一些未探索的方法。从表3中可以看出，还没有任何联合和构造算法来解决 Bin Packing 问题的方法被发表。可以将相同的逻辑应用于表 3 的最小顶点问题，其中没有联合构造和联合非构造类型的方法。探索这些算法的可能性不仅可以为我们提供新方法，而且还可以为我们提供有关这些方法有效性的有用见解。 

总之，与传统的启发式方法相比，由于解决方案质量方面的有效性、优于现有算法的能力以及巨大的运行时间收益，我们可以看到将 RL 用于 CO 问题的领域对于 CO 研究来说是非常有希望的方向。 

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

???? 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

???? 投稿邮箱：

• 投稿邮箱：[email protected] 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

????

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。