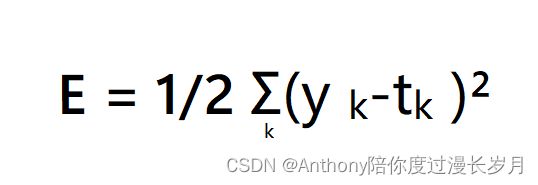“深度学习”学习日记。神经网络的学习--损失函数
2023.1.8
昨天预习了一下神经网络的学习的内容,神经网络的学习中的“学习”是指从训练中自动获取最优权重参数的过程。这里以后会学习到损失函数和函数斜率的梯度法。
为了使神经网络学习,就得导入损失函数这一个指标。而学习的目的就是一该损失函数为基准,找出使它的值达到最小权重的参数。
在利用感知机去实现数字电路的逻辑门的只由几个参数需要人工确定,而在MNIST识别任务中,我们面对不同的数字由不同的权重,这些权重都需要人工去确定是效率极低且不科学的,对此,神经网络的面对所有的问题都是用同样的流程来解决,都是通过不断地学习提供的数据,尝试发现待求解的问题的模式。至此,深度学习也被称为端到端的机器学习,即从原始数据中获得目标结果的模型
训练数据和测试数据
机器学习中,一般将数据分为训练数据和测试数据来进行学习和实验(训练数据也被称为监督数据)。首先,得用训练数据去进行学习,找出最佳参数;然后,使用测试数据去评价训练得到得模型的能力
对于评价训练所得的模型的能力,需要引入泛化能力这一个概念,泛化能力比如MNIST识别模型可以很好的去识别手写数字,对此我们将这个模型引用到邮政编码的识别上,“邮政编码”在此也被称为未被观察过的数据。
一个神经网络模型的泛化能力越强这代表它的实际能力也越强,这也是我们将数据分为数据和测试数据的原因。
此外,不能仅仅使用一个数据集去学习和评价参数,这样会出现过拟合现象
损失函数
“神经网络的学习”通过某个指标表示现在的状态(即当前的神经网络对监督数据在多大程度上不拟合、在多大程度上不一致),然后,再以这个指标为基准,寻找最优权重参数。而这个指标称为损失函数,它可以使是任意函数,一般是使用 均方误差 和 交叉熵误差
均方误差
y是神经网络的输出,t是监督数据,k是数据的维度
import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum((y - t) ** 2)
# y表示神经网络的输出,是测试数据经过神经网络的分类概率结果
# t是监督数据,是利用训练数据得到的分率概率结果
# 假设 一个·输出分类概率数组y与相对于正确解标签的监督数据t
y = [0.01, 0.03, 0.7, 0.06, 0.2, 0.0, 0.0, 0.0, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
print(mean_squared_error(np.array(y), np.array(t)), '\n') # 0.06730000000000003
# 假设 “2”为正确劫标签,即t
y2 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] # 输出学习分类概率最大的情况为’2‘
y3 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.0, 0.6, 0.0] # 输出学习分类概率最大的情况为’8‘
print(mean_squared_error(np.array(y2), np.array(t))) # 0.09750000000000003
print(mean_squared_error(np.array(y3), np.array(t))) # 0.5974999999999999通过代码实验可以知道,均方误差的值越小表示神经网络模型的学习效果越好 ,输出结果与监督数据更加吻合。
交叉熵误差
y是神经网络的输出,t是监督数据,k是维度
可以知道,x等于1是,y等于0; 当出现np.log(0)时,delta这个微小值可以防止出现-inf而无法计算
import numpy as np
import matplotlib.pyplot as plt
# y表示神经网络的输出,是测试数据经过神经网络的分类概率结果
# t是监督数据,是利用训练数据得到的分率概率结果
# 假设 一个·输出分类概率数组y与相对于正确解标签的监督数据t
y = [0.01, 0.03, 0.7, 0.06, 0.2, 0.0, 0.0, 0.0, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 假设 “2”为正确劫标签,即t
y2 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] # 输出学习分类概率最大的情况为’2‘
y3 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.0, 0.6, 0.0] # 输出学习分类概率最大的情况为’8‘
def cross_entropy_error(y, t):
delta = 1e-7
return -1 * np.sum(t * np.log(y + delta))
print(cross_entropy_error(np.array(y2), np.array(t))) # 0.510825457099338
print(cross_entropy_error(np.array(y3), np.array(t))) # 2.302584092994546由此可以看出,这里和交叉熵误差的值越小表示神经网络模型的学习效果越好 ,输出结果与监督数据更加吻合。