支持向量机(SVM),原理推导
写在前头:
本文综合各家之长,尽可能的让自己明白;若有错误之处,请网友指出,谢谢。
原文地址:https://blog.csdn.net/yuxiaoye03222/article/details/108269311
https://www.likecs.com/show-203769929.html
支持向量机是一个有监督学习算法,可用来进行模式识别、二分类、回归分析。如图有两堆二维数据,数据有BCD等无数种分割线,我们要找的是泛化能力最好的分割线;类比到三维空间中,则是一个面;在多维空间中,我们把它称为超平面。

一、什么是泛化能力最好的分割超平面
以上图中的小图D为例,我们把距离分割线最近的点叫做支持向量,那么使支持向量到分割线的距离最大的直线就是我们要找的、泛化能力最好的超平面。SVM的核心内容就是最大化这个距离,并求超平面的函数(即求超平面的参数)。
二、空间中任一点x到超平面的距离为:
r = ∣ W T X + b ∣ ∣ ∣ W ∣ ∣ r=\frac{|W^TX+b|}{||W||} r=∣∣W∣∣∣WTX+b∣,其中W为超平面的参数矩阵。
其推导过程如下:
在二维空间中,线的函数表达式为Ax+By+C=0;三维空间中面的表达式为Ax+By+Cz+D=0;所以类比到多维空间中,超平面的表达式为 W T X + b = 0 W^TX+b=0 WTX+b=0;我们以二维空间中点到直线的距离来类比到多维空间中。
如下图,设过原点的直线L: W T X + b = 0 W^TX+b=0 WTX+b=0,其中W为线的法向量;则坐标向量A到直线L的距离即为A向量在W向量上投影的模长
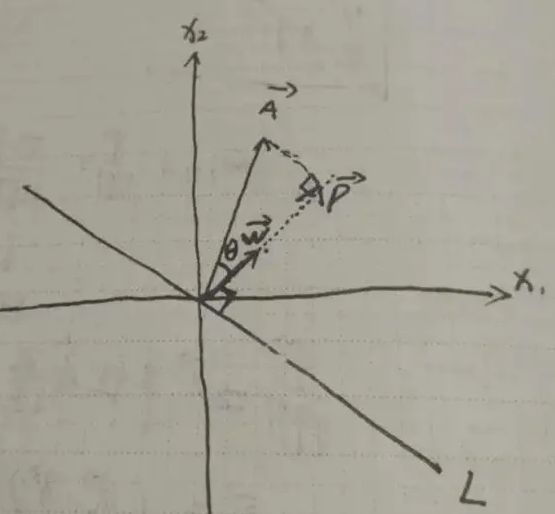
W的单位方向向量为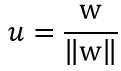 ,其中||W||表示W向量的模长,所以||u||=1。
,其中||W||表示W向量的模长,所以||u||=1。
P的模长 ||P|| = ||A||cosθ(1)
又因为u•A = ||u||||A||*cosθ = ||A||*cosθ(2)
再推导一下A点到不过原点的直线L的距离:
设有直线L:W(m,n),X(x1,x2),直线L为m* x1+n*x2+b=0,截距-b/n,K向量为(0, - b/n) ,坐标向量A。所以:
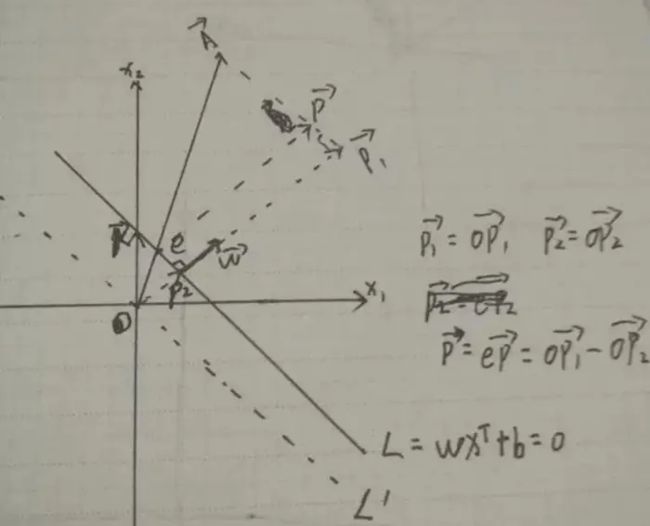
||P2||=(W•K)/(||W||)=((0,(-b)⁄n)•(m,n))/(||W||)=(-b)/(||W||)
||P1||=(W•A)/(||W||)
||P||=||P1||-||P2||=(W•A)/(||W||)-(-b)/|(|W| )| =(W•A+b)/(||W||)
所以间隔 m=|W^t A+b|/||W||。
如上图所示,x到x’的距离*超平面的单位法向量就是点x到超平面的距离。上图中浅黄色部分中的公式(x-x’)表示点x到x’的距离,是一种坐标轴表示。
三、确定目标函数:即找到求解W、b的函数。
1、与逻辑回归类似,我们人为定义:当X为正例时,标签Y=+1;当X为负例时,标签Y=-1(定义为±1仅是为了后续计算方便)。则超平面方程为:
y ( x ) = W T Φ ( x ) + b y(x)=W^TΦ(x)+b y(x)=WTΦ(x)+b,其中 Φ ( x ) Φ(x) Φ(x)为样本点非线性可分时,对样本点进行的转换。
因为我们上面已经定义:当X为正例时,标签Y=+1;当X为负例时,标签Y=-1。所以可得到下面这个恒成立的不等式。
 重点: y i . y ( x i ) > 0 y_i.y(x_i)>0 yi.y(xi)>0很重要,它是我们下面推导过程的条件限制的雏形。
重点: y i . y ( x i ) > 0 y_i.y(x_i)>0 yi.y(xi)>0很重要,它是我们下面推导过程的条件限制的雏形。
由上公式可知 y i y_i yi的值只有1和-1,把它代入距离公式,即不影响结果,还能去掉绝对值,故距离公式变为:
y i . ( W T . Φ ( x i ) + b ) ∣ ∣ W ∣ ∣ \frac{y_i.(W^T.Φ(x_i)+b)}{||W||} ∣∣W∣∣yi.(WT.Φ(xi)+b),条件是 y i . y ( x i ) > 0 y_i.y(x_i)>0 yi.y(xi)>0。
2、放缩变换:对于决策方程(W,b)可以通过放缩使得其结果值|Y|>=1,即:
=> y i . ( W T . Φ ( x i ) + b ) ≥ 1 y_i.(W^T.Φ(x_i)+b)≥1 yi.(WT.Φ(xi)+b)≥1,之前我们得到恒>0的条件,现在我们进一步限制条件,使得优化目标可求解。
3、确定优化目标:
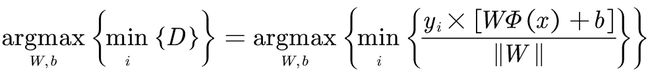
其中, min i ( D ) \displaystyle\min_{i}(D) imin(D)依次遍历样本点,找到最近的间隔,即找到支持向量到超平面的距离; arg max w , b \displaystyle\argmax_{w,b} w,bargmax指找到W,b的值,使支持向量到超平面的距离最远。
由于上面限制了条件 y i . ( W T . Φ ( x i ) + b ) ≥ 1 y_i.(W^T.Φ(x_i)+b)≥1 yi.(WT.Φ(xi)+b)≥1,则优化目标可化简为:
arg max w , b 1 ∣ ∣ W ∣ ∣ \displaystyle\argmax_{w,b}\frac{1}{||W||} w,bargmax∣∣W∣∣1,当 y i . ( W T . Φ ( x i ) + b ) ≥ 1 y_i.(W^T.Φ(x_i)+b)≥1 yi.(WT.Φ(xi)+b)≥1。条件很重要,它是优化目标成立的前提。
四、求解目标函数
1、思路: 机器学习中,通常将求解极大值问题转换成极小值问题(常规套路了)。
2、转化目标函数: 所以,我们可以将目标函数
arg max w , b 1 ∣ ∣ W ∣ ∣ \displaystyle\argmax_{w,b}\frac{1}{||W||} w,bargmax∣∣W∣∣1,约束条件: y i . ( W T . Φ ( x i ) + b ) ≥ 1 y_i.(W^T.Φ(x_i)+b)≥1 yi.(WT.Φ(xi)+b)≥1
转化为: min w , b 1 2 W 2 \displaystyle\min_{w,b}\frac{1}{2}W^2 w,bmin21W2 (本人不太明白转换过程,只知道是为了方便求解)
3、求解方法:拉格朗日乘子法。
拉格朗日乘子法的思路是:直接求解W、b的参数不好求解,可以先转换成求解与W、b有关系的α(是个矩阵);求出α即可求出W、b。
小白不知道咋求得,只知道将转换后得目标函数代入“带条件限制的拉格朗日乘子公式”,再分别对W和b求偏导,利用对偶性质(由KKT三人提出,推导过程非常非常复杂,完全看不懂)求解W、b分别关于α的表达式,然后将W、b代入原式,这样目标函数就转化为关于α的问题。
接下来就转化为对α求极大值,老套路了,再转化为求α的极小值问题。最终得到关于α的求极小值的函数为:
min α 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( Φ ( x i ) . Φ ( x j ) ) − ∑ i = 1 n α i \displaystyle\min_α\frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n} α_iα_jy_iy_j(Φ(x_i).Φ(x_j))-\displaystyle\sum_{i=1}^{n}α_i αmin21i=1∑nj=1∑nαiαjyiyj(Φ(xi).Φ(xj))−i=1∑nαi
约束条件为: ∑ i = 1 n α i y i = 0 \displaystyle\sum_{i=1}^{n}α_iy_i=0 i=1∑nαiyi=0, α i ≥ 0 α_i≥0 αi≥0
4、举个简单的例子演示W、b的求取过程
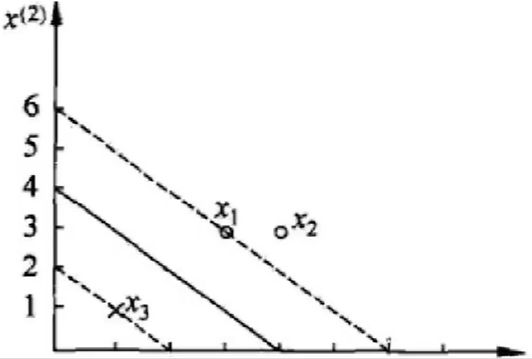
如上图所以,有3个点:正例 x 1 x_1 x1(3,3)、 x 2 x_2 x2(4,3);负例 x 3 x_3 x3(1,1)。求决策边界:
优化函数为: 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( Φ ( x i ) . Φ ( x j ) ) − ∑ i = 1 n α i \frac{1}{2}\displaystyle\sum_{i=1}^{n}\displaystyle\sum_{j=1}^{n} α_iα_jy_iy_j(Φ(x_i).Φ(x_j))-\displaystyle\sum_{i=1}^{n}α_i 21i=1∑nj=1∑nαiαjyiyj(Φ(xi).Φ(xj))−i=1∑nαi
约束条件为: α 1 + α 2 − α 3 = 0 α_1+α_2-α_3=0 α1+α2−α3=0,
α i ≥ 0 α_i≥0 αi≥0, i = 1 , 2 , 3 i=1,2,3 i=1,2,3
将3个数据点代入公式得:
1 2 ( 18 α 1 2 + 25 α 2 2 + 2 α 3 2 + 42 α 1 α 3 − 12 α 1 α 3 − 14 α 2 α 3 ) − α 1 − α 2 − α 3 \frac{1}{2}(18α_1^2+25α_2^2+2α_3^2+42α_1α_3-12α_1α_3-14α_2α_3)-α_1-α_2-α_3 21(18α12+25α22+2α32+42α1α3−12α1α3−14α2α3)−α1−α2−α3
由于: α 1 + α 2 = α 3 α_1+α_2=α_3 α1+α2=α3,化简上式得: 4 α 1 2 + 13 2 α 2 2 + 10 α 1 α 2 − 2 α 1 − 2 α 2 4α_1^2+\frac{13}{2}α_2^2+10α_1α_2-2α_1-2α_2 4α12+213α22+10α1α2−2α1−2α2
分别对 α 1 α_1 α1和 α 2 α_2 α2求偏导,令偏导等于0可得: α 1 = 1.5 α_1=1.5 α1=1.5、 α 2 = − 1 α_2=-1 α2=−1;不满足 α i ≥ 0 α_i≥0 αi≥0, i = 1 , 2 , 3 i=1,2,3 i=1,2,3;所以此解不成立。
所以应考虑一些边界情况(不懂为何要考虑边界情况),分别尝试代入 α 1 = 0 , α 2 = 0 α_1=0,α_2=0 α1=0,α2=0等,求得:
当 α 1 = 0 α_1=0 α1=0时,对 α 2 α_2 α2求偏导得 α 2 = − 2 13 α_2=-\frac{2}{13} α2=−132,不满足条件;
当 α 2 = 0 α_2=0 α2=0时,对 α 1 α_1 α1求偏导得 α 1 = 0.25 α_1=0.25 α1=0.25,代入得 α 3 = 0.25 α_3=0.25 α3=0.25满足条件。
所以最小值在(0.25,0,0.25)处取得。
将α结果代入 W = ∑ i = 1 n α i y i Φ ( x n ) W=\displaystyle\sum_{i=1}^{n}α_iy_iΦ(x_n) W=i=1∑nαiyiΦ(xn),求解:
W = 1 4 ∗ 1 ∗ ( 3 , 3 ) + 1 4 ∗ ( − 1 ) ∗ ( 1 , 1 ) = ( 1 2 , 1 2 ) W=\frac{1}{4}*1*(3,3)+\frac{1}{4}*(-1)*(1,1)=(\frac{1}{2},\frac{1}{2}) W=41∗1∗(3,3)+41∗(−1)∗(1,1)=(21,21)
b = y i − ∑ i = 1 n α i y i ( x i y i ) = 1 − ( 1 4 ∗ 1 ∗ 18 + 1 4 ∗ ( − 1 ) ∗ 6 ) = − 2 b=y_i-\displaystyle\sum_{i=1}^{n}α_iy_i(x_iy_i)=1-(\frac{1}{4}*1*18+\frac{1}{4}*(-1)*6)=-2 b=yi−i=1∑nαiyi(xiyi)=1−(41∗1∗18+41∗(−1)∗6)=−2
得超平面方程为: 0.5 x 1 + 0.5 x 2 − 2 = 0 0.5x_1+0.5x_2-2=0 0.5x1+0.5x2−2=0
五、软间隔-松弛因子
前面我们求最大间隔时,是在 y i y ( x i ) > 0 y_iy(x_i)>0 yiy(xi)>0的条件下进行的,它隐含的意思是要把样本完全分开、分正确;在实际应生活中,很难用一个平面将数据严格地分成两类,有些孤立点(或称离群点、异常点)会影响到决策面。所以,我们想忽略掉这些异常点去分割数据,故引入松弛因子,即:
y i ( W . X i + b ) ≥ 1 − ξ i y_i(W.X_i+b)≥1-ξ_i yi(W.Xi+b)≥1−ξi
1、目标函数
引入松弛因子后,目标函数变为:
m i n 1 2 ∣ ∣ W ∣ ∣ 2 + C ∑ i = 1 n ξ i min\frac{1}{2}||W||^2+C\displaystyle\sum_{i=1}^nξ_i min21∣∣W∣∣2+Ci=1∑nξi
C是我们需要指定的一个参数:
当C趋于很大时,意味着分类严格不能有错误
当C趋于很小时,意味着可以有更大的错误容忍度
2、求解目标函数
跟之前的一样,利用拉格朗日乘子法和对偶性进行求解,反正我也不会求。
六、核函数-低维度不可分问题
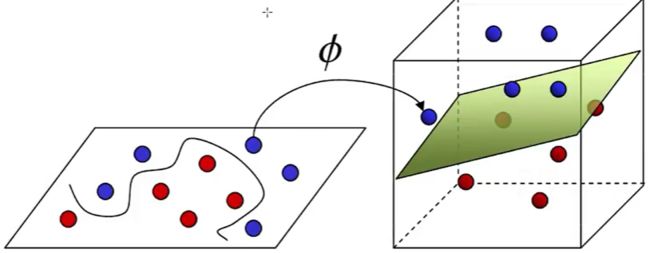
如上图所示,红、蓝点在二维空间上分割较困难,若强行分割,则会导致模型过于复核和出现过拟合风险。但投射到三维空间,则分割较容易、且准确率高。核函数变换就是处理低维不可分问题的,这也是支持向量机优于其它分类算法、称霸武林的原因。
1、定义: 核变换:有的样本低维不可分,映射到高维则可分
2、如何变换: 高斯核函数
常规思路是将低维向量先映射到高维向量,再求解;但,求解过程涉及到内积运算,维度过高,计算量非常大,比如3维映射到9维,计算量是幂级增长;若实际运用中,维度再增加,则很难求解。
所以转换思路,先将低维向量求内积,再映射到高维空间,若结果不变,则方法可行;而实现这个想法的函数被称为核函数。在实践中,确实存在这种核函数,但种类比较少,最常见的是高斯核函数(常用)、多向量核函数(没见有人用过)。
高斯核函数: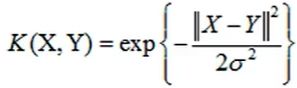 本质是做个高斯变换,即把原始数据特征映射成高斯函数中的距离特征。
本质是做个高斯变换,即把原始数据特征映射成高斯函数中的距离特征。
