支持向量机SVM与SMO算法的的详细推导过程

SVM简介与背景知识

通俗来说，支持向量机就是一个二分类问题，根据所给的训练集数据集进行将数据的最佳划分，以达到测试集的最佳分类。支持向量机也叫做SVM，在实际工业的运用中，有着很强的可靠性和广泛的使用。接下来我们就来具体介绍一下这么好用的算法。


所谓的二分类问题就是通过一条分割线来对数据进行分类，在二维情况下就是平面直角坐标系下的y=kx+b，当x的维度（对应与需要分类的条件，即属性增多的情况）大于等于2时，情况就上升的多维的情况，我们就引出了超平面的概念。当数据集带入线性可分的方程之后，通过判断y的值，进而对数据集进行划分。大于0则属于第一类，小于0属于第二类。需要指出的是，SVM是一个线性的分类问题，因为其简单所以大量应用，对于更复杂的问题，我们可以采用非线性的划分，但在这里不做讨论。
那么我们这么确定这条直线呢，确定的约束又是什么呢？



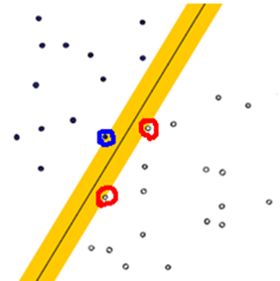
这里，我们就可以引出支持向量和支持向量机的概念了。
支持向量（support vector）就是离分隔超平面最近的那些点。接下来要试着最大化支持向量到分隔面的距离，需要找到此问题的优化求解方法。

 支持向量机 ：
优点：泛化错误率低，计算开销不大，结果易解释。
缺点：对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于处理二类问题。
适用数据类型：数值型和标称型数据

SVM的数学证明

在介绍完背景知识后，就可以引出公式和数学证明了。数学功底好的读者可以阅读本部分，了解其原理，如果只是想了解概念和代码的，可以跳过本部分，直接最后的算法和代码部分。
先给出点到直线的距离公式，以便后续的使用


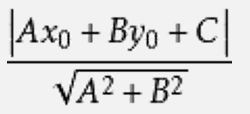
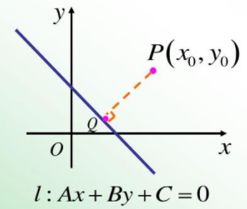
我们指出，最佳的直线应该是最能分割数据集的点的直线，即使得直线的最近的数据点之间的距离要最大！所以我们主要就是对支持向量和最大间隔进行讨论。

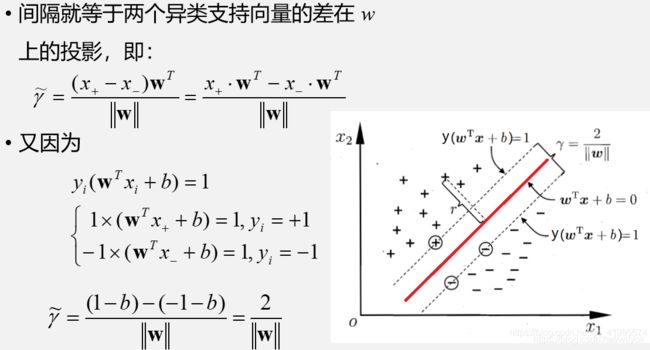
上面就是两个方程组相减最为点到直线距离的公式的分母，因为结果为正，所以没有加绝对值
其中根据公式，wx=±1+b的，所以带入计算得结果为2（分子）

我们要使其最大，就要w最小也即0.5*w^2(w是一个向量)，因此转化为求最小值的问题（带有约束条件）
因此我们就将问题转化为了一个带约束的二次规划问题，它是一个凸问题。而对于优化问题，我们可以使用拉格朗日乘子法去解决它。


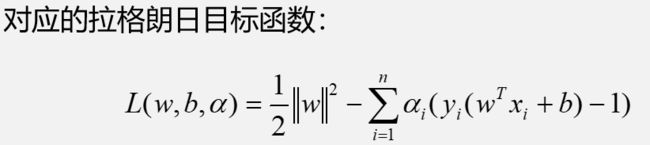
接下来我们就对上述引出的拉格朗日函数进行分步骤求解，并最终导出公式
第一步，对自变量求偏导


在求出偏导方程之后，也就是取得极值时候的对应变量应取得的条件，把它带回原方程

现在回到问题的根本，我们的目标是求最小间隔的最大化问题
目前为止计算得出的是，对应w下，最小间隔，接着我们要计算α使得最小间隔最大化成立

下面再补充一些对偶问题的定理：

原问题:min x max a,b L(x,a,b)
对偶问题 max a,b min x L(x,a,b)
在普通的约束条件下，这两个问题的解满足性质：原问题>=对偶问题
特殊情况：当等号成立的时候，应满足如下四个条件
①方程对自变量x的求导方程=0
②约束条件αig(xi) = 0
③gi(x)<=0
④αi>=0
⑤约束条件是线性的
⑥原问题是一个凸问题
其中①-④为kkt条件

由于有了对偶定理的存在，就保证了分别求解max 和min之后问题的解是一样的

由对偶的性质，我们可以将其转换为对偶问题


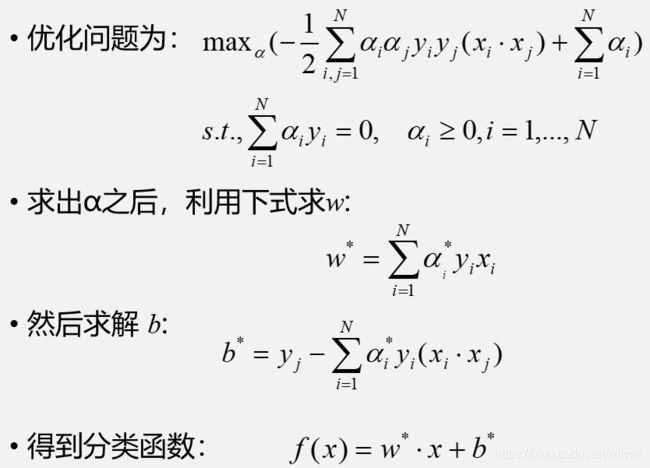
这样，我们就完成了对最基本问题的求解，但它不适用与大多数情况，我们进行如下讨论。
其实在很多时候，不是在训练的时候分类函数越完美越好，因为训练函数中有些数据本来就是噪声，可能就是在人工加上分类标签的时候加错了,如果在训练(学习)的时候把这些错误的点学习到了，那么模型在下次碰到这些错误情况的时候就难免出错了。这种学习的时候学到了“噪声" 的过程就是一个过拟合(over-iting) ， 这在机器学习中是一一个大忌， 宁愿少学-些内容， 也坚决杜绝多学-些错误的知识。

这种加入了惩罚函数的算法，才是最终我们代码里要介绍的简化版SMO算法，接下来我们就对其进行原理上的推导。


因此，我们的目标函数和约束条件就变成了下面的这个样子：


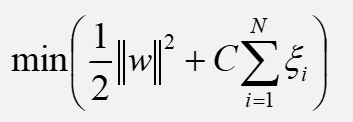
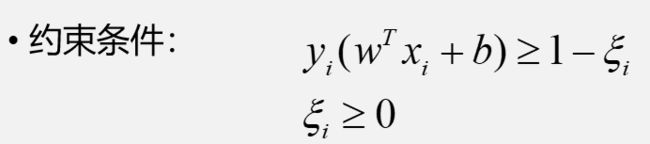
接下来我们对目标函数和约束条件进行进一步的化简，以便最终得出可执行的算法

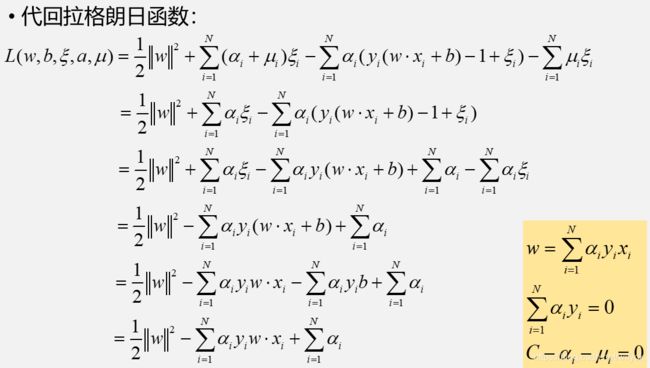
简化版SMO算法

所谓的SMO算法就是序列最小最优化算法

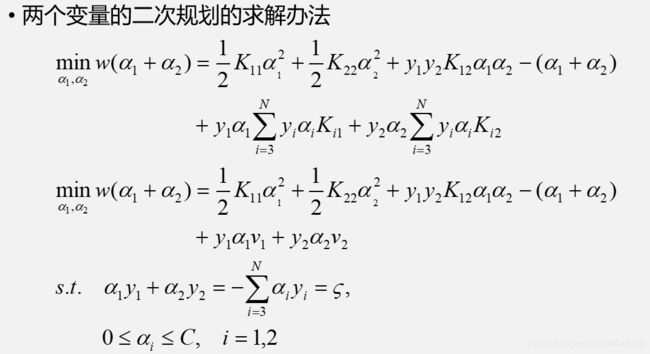
其中，K11代表向量x1与x1点成的结果，或者表示输入为x1，x1的核函数的结果
上图还将目标函数的一系列求和部分用v1和v2代替了，读者注意一下这里的替换


接下来就对之前的v1和v2作具体的说明



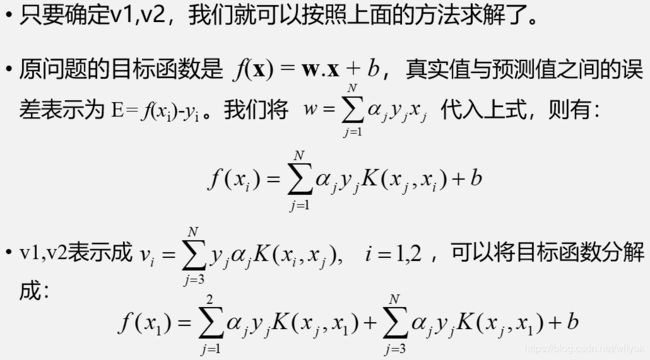
由此就得出了α2 new的计算公式，根据old推出new

该SMO函数的伪代码大致如下：
创建一个alpha向量并将其初始化为0向量
当迭代次数小于最大迭代次数时（外循环）
对数据集中的每个数据向量（内循环）：
如果该数据向量可以被优化：
随机选择另外一个数据向量
同时优化这两个向量
如果两个向量都不能被优化，退出内循环
如果所有向量都没被优化，增加迭代数目，继续下一次循环

代码实现

导入数据集

def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

选择α

def selectJrand(i,m):
    j=i #we want to select any J not equal to i
    while (j==i):
        j = int(random.uniform(0,m))
    return j

保证数据的有效性

def clipAlpha(aj,H,L):
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj

简化版SMO算法

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
    b = 0; m,n = shape(dataMatrix)
    alphas = mat(zeros((m,1)))
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i,m)
                fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print("eta>=0"); continue
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); continue
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
                                                                        #the update is in the oppostie direction
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        print("iteration number: %d" % iter)
    return b,alphas