基于MATLAB的手写体数字识别算法的实现
基于MATLAB的手写体数字识别
一、课题介绍
手写数字识别是模式识别领域的一个重要分支,它研究的核心问题是:如何利用计算机自动识别人手写在纸张上的阿拉伯数字。手写体数字识别问题,简而言之就是识别出10个阿拉伯数字,由于数字的清晰程度或者是个人的写字习惯抑或是其他,往往手写体数字的性状、大小、深浅、位置会不大一样。手写体识别一般包括3个阶段:预处理、特征提取、分类识别。
手写数字识别前景广阔,广泛应用于表格中数字的识别、汽车牌照的数字自动识别和成绩单的识别等。实现数字的自动识别能够给人们的工作和生活带来很大的方便。对于该领域的研究具有重要的理论价值:
一方面,阿拉伯数字是唯一的被世界各国通用的符号,对手写数字识别的研究与文化背景无关,这样就为各国、各地区的研究工作者提供了一个自由平等的舞台,大家可以在这一领域施展才智,各抒己见。
另一方面,由于数字识别的类别数较少(只有0到9十个类别),有助于做深入分析及验证一些新的理论。这方面最明显的例子就是人工神经网络,相当一部分的人工神经网络模型都以手写数字识别作为具体的实验平台,验证理论的有效性,评价各种方法的优缺点。
数字识别的算法较多,当前运用较好的主流算法以统计、聚类和分类算法为主,如Bagging算法、支持向量机算法、神经网络等。手写数字识别难度在于:一、数字相似性大,但字形相差不大;二、数字虽然只有10种,但笔划简单,同一个数字写法差别大;三、手写数字存在断笔和毛刺,对识别造成影响。本文选择分类算法中的决策树算法、支持向量机算法、神经网络对MNIST数据集进行数字识别,并对分类效果进行比较分析。
分类算法
分类器识别是实现手写体数字识别的最终关键,基于距离的分类器和神经网络分类器这两大类是目前现有的最主要的分类器。分类是数据挖掘的重要分支,可用于提取、描述重要数据的模型或预测未来的数据趋势[1]。
决策树算法
决策树也称为判定树,是一种有监督的学习方法。决策树代表着决策树的树形结构,可以根据训练集数据构造出决策树。如果该树不能对所有对象给出正确的分类,就选择一些例外加入到训练集数据中。重复该过程,直到形成正确的决策集。决策树方法首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策树对新数据进行分析,本质上是通过一系列规则对数据进行分类的过程。决策树的典型算法有ID3,C4.5,等。根据训练集构建决策树,决策树中的结点逐层展开。每展开一层子结点,并将其设为叶结点,就得到一棵决策树,然后采用测试集对所得决策树的分类性能进行统计。重复上述过程,可以得到决策树在测试集上的学习曲线。根据学习曲线,选择在测试集上性能最佳的决策树为最终的决策树。
2.1.1 ID3算法
J.Ross Quinlan在1986年将信息论引入到决策树算法中,提出了ID3[2]算法,算法思想如下:
设样本集E共有C类训练集,每类样本数为pi,且i=1,2,3,…,C。如果以属性A作为测试属性,属性A的v个不同的值为{v1,v2,…,vv},可以用属性A将E划分成v个子集{E1,E2,…,Ev},假定Ei中含有第j类样本的个数为pij,j=1,2,3,…,C,那么子集Ei的熵为:
(1)
属性A的信息熵为:
(2)
将代入公式(2)后可得:
(3)
一棵决策树对一实例做出正确类别判断所需的信息为:
(4)
信息增益:
ID3算法存在着属性偏向,对噪声敏感等问题。
2.1.2 C4.5算法
在ID3算法的基础上,Quinlan在1993年提出了一种改进的算法,即C4.5算法[3],信息增益率计算如下:
(5)
(6)
C4.5算法克服了ID3算属性偏向的问题,增加了对连续属性的处理,通过剪枝,在一定程度上避免了“过度拟合”的现象。但是该算法将连续属性离散化,需要遍历该属性的所有值,降低了效率;要求训练样本驻留在内存,不适合处理大规模数据集。
2.1.3 CART算法
CART算法可以处理无序的数据,采用基尼系数作为测试属性的选择标准,基尼系数的计算如下:
(7)
其中,
,pi是类别j在T中出现的概率。
CART算法生成的决策树精度较高,但是当其生成的决策树复杂度超过一定程度后,随着复杂度的提高,分类精确度会降低。因此,用该算法建立的决策树不宜太复杂[4]。
2.1.4 SLIQ算法
决策树分类算法研究一直朝着处理大数据集的方向进行,但大部分方法在减少了运算时间的同时也降低了算法的精度。SLIQ的分类精度与其他决策树算法不相上下,但其执行的速度比其他决策树算法快。SLIQ算法对训练样本集的样本数量以及属性的数量没有限制。
SLIQ算法能够处理大规模的训练样本集,具有较好的伸缩性;执行速度快而且能够生成较小的二叉决策树;SLIQ算法允许多个处理器同时处理属性表,从而实现并行性。但是SLIQ算法不能摆脱主存容量的限制。
2.1.5 SPRINT算法
SLIQ算法要求类表驻留内存,当训练集大到类表放不进内存时,SLIQ算法就无法执行。为此,IBM的研究人员提出SPRINT算法,它处理速度快,不受内存的限制。
SPRINT算法可以处理超大规模训练样本集,数据样本集数量越大,SPRINT的执行效率越高,并且可伸缩性更好。但是,SPRINT算法存在着一些缺陷,在SLIQ的类表可以存进内存时,SPRINT算法的执行速度比SLIQ算法慢。
2.1.6 经典决策树算法的比较
基于决策树的分类算法已经有几十种,各种算法在执行速度、可扩展性、输出结果的可理解性、分类预测的准确性方面各有所长。下面就对几种典型的决策树算法进行比较,结果如表2-1所示:
表2-1 典型决策树算法的比较
| 算法 | 测试属性选择指标 | 连续属性的处理 | 是否需要独立测试样本集 | 运行剪枝时间 | 可伸缩性 | 并行性 | 决策树的结构 |
| ID3 | 信息增益 | 离散化 | 是 | 后剪枝 | 差 | 差 | 多叉树 |
| C4.5 | 信息增益率 | 预排序 | 否 | 后剪枝 | 差 | 差 | 多叉树 |
| CART | GINI系数 | 预排序 | 否 | 后剪枝 | 差 | 差 | 二叉树 |
| SLIQ | GINI系数 | 预排序 | 否 | 后剪枝 | 良好 | 良好 | 二叉树 |
| SPRINT | GINI系数 | 预排序 | 否 | 后剪枝 | 好 | 好 | 二叉树 |
支持向量机
支持向量机(SVM)方法是通过一个非线性p,把到一个乃至无穷维的特征空间中(Hilbert空间),使得在原来的中非线性可分的问题转化为在特征空间中的线性可分的问题.简单地说,就是升维和线性化。升维,就是把样本向高维空间做映射,一般情况下这会增加计算的复杂性,甚至会引起"",因而人们很少问津.但是作为分类、回归等问题来说,很可能在低维样本空间无法线性处理的样本集,在高维特征空间中却可以通过一个线性超平面实现线性划分(或回归).一般的升维都会带来计算的复杂化,SVM方法巧妙地解决了这个难题:应用的展开定理,就不需要知道非线性映射的显式表达式;由于是在高维特征空间中建立线性学习机,所以与相比,不但几乎不增加计算的复杂性,而且在某种程度上避免了"维数灾难".这一切要归功于核函数的展开和计算理论。选择不同的,可以生成不同的SVM。
SVM的机理是寻找一个满足分类要求的最优分类超平面,使得该超平面在保证分类精度的同时,能够使超平面两侧的空白区域最大化。
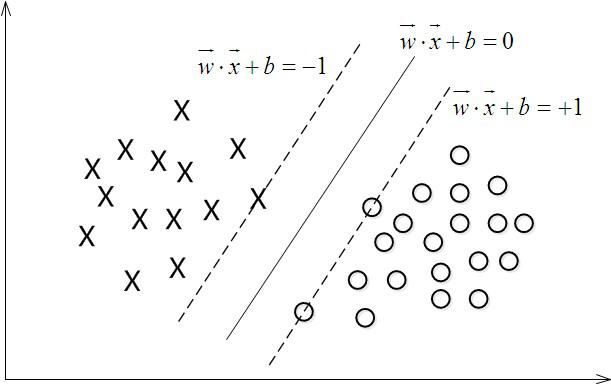
理论上,支持向量机能够实现对线性可分数据的最优分类。以两类数据分类为例,给定训练样本集(xi,yi),i=1, 2,⋅⋅⋅,l,x∈Rn,y∈{±1},超平面记作(w · xi)+b=0,为使分类面对所有样本正确分类并且具备分类间隔,就要求它满足如下约束:yi[(w · xi)+b]≥1,i=1,2,…,l。
图2-1 支持向量机
可以计算出分类间隔为2/||w||,因此构造最优超平面的问题就转化为在约束式下求:
(8)
为了解决该个约束最优化问题,引入Lagrange函数:
(9)
式中,ai>0为Lagrange乘数。约束最优化问题的解由Lagrange函数的鞍点决定,并且最优化问题的解在鞍点处满足对w和b的偏导为0,将该QP问题转化为相应的对偶问题即:
(10)
解得最优解
(11)
计算最优权值向量w*和最优偏置b*,分别为:
(12)
因此得到最优分类超平面(w*·x) +b*=0,而最优分类函数为:
(13)
对于线性不可分情况,SVM的主要思想是将输人向量映射到一个高维的特征向量空间,并在该特征空间中构造最优分类面。将x做从输入空间Rn到特征空间H的变换Φ,得:
(14)
以特征向量Φ(x)代替输入向量x,则可以得到最优分类函数为:
(15)
在上面的对偶问题中,无论是目标函数还是决策函数都只涉及到训练样本之间的内积运算,在高维空间避免了复杂的高维运算而只需要进行内积运算。
人工神经网络
人工神经网络是指模拟人脑神经系统的结构和功能,运用大量的处理部件,由人工方式建立起来的网络系统。该网络具有大规模并行协同处理能力和较强的容错能力和联想能力,同时是一个具有较强学习能力的大规模自组织、自适应性的非线性动力系统。
2.3.1人工神经网络的原理
神经网络的结构是基本处理单元及其互连方法决定的。如图所示,单个神经元单元由多个输入xi,i=1,2,...,n和一个输出y组成。
图3-2 神经元
(16)
式中,为神经元单元的偏置(阈值),wi为连接权系数,n为输入信号数目, y为神经元输出,f为输出变换函数,称为激活函数。
2.3.2反向传播网络(BP)
BP网络是一类典型的前馈网络。其它前馈网络有感知器(Perception)、自适应线性网络和交替投影网络等。前馈网络是一种具有很强学习能力的系统,结构比较简单,且易于编程。前馈网络通过简单非线性单元的复合映射而获得较强的非线性处理能力,实现静态非线性映射。BP网络主要特点是能够实现从n维到m维的非线性映射,它还可以采用梯度下降法实现快速收敛。模型如下图所示:
图3-3 反向传播网络
反向传播算法的具体流程如下:
(1)对于给定的样本集
,初始化网络结构
。初始化权系数
,学习率η,阈值
。
(2)根据样本集D更新权系数
:
(17)
(18)
(3)计算
,如果
结束训练,并认为此时的
为最优。否则转第2步继续进行循环。
对于反向传播模型的初始化如下:
输入层:单元i的输入:xi
单元数量:d
单元i的输出:xj
单元i的激活函数:线性函数
隐 层:单元j的净输入:netj
单元数量:nH
单元j的输出:yj
单元j的激活函数:非线性函数
输出层:单元k的净输入:netk
单元数量:c
单元k的输出:zk
单元k的激活函数:非线性函数
(1)学习速率
学习速率
直接影响权系数调整时的步长。学习速率过小,导致算法收敛速度缓慢。学习速率过大,导致算法不收敛。学习速率的典型取值
。另外学习速率可变。误差函数的局部极小值调整权系数的目标是使误差函数取得最小值。但是,采用梯度下降法(Gradient Descent Procedure)不能保证获得最小值,而只能保证得到一个极小值。如果训练过程无法使误差函数降低到预期的程度,一种常用的方法是:再一次对权系数进行随机初始化,并重新训练网络。
(2)学习曲线
样本集的划分:一般情况下,可把已知的样本集划分为三个子集,即训练集、确认集、测试集。
训练集:用来调整权系数,使误差函数尽可能变小。确认集:用来初步验证神经网络对未来新样本的分类能力,并据此确定最佳的权系数。神经网络的训练过程需要采用训练集及确认集共同完成。
测试集:在训练过程最终结束后,再采用测试集对网络的分类性能进行最后测试,用以评估神经网络在实际应用中的实际性能。
2.3.3 Hopfield网络
Hopfield网络是一种动态反馈系统,可以用一个完备的无向图表示,它比前馈网络具有更强的计算能力。
Hopfield网络一般只有一个神经元层次,每个神经元的输出都与其它神经元的输入相连,是一种单层全反馈网络。如图3-4所示。
图3-4 Hopfield网络
Hopfield网络中神经元之间的权值一般是对称的。但每个神经元都没有到自身的联接。神经元i和神经元j之间相互连接的权值相等,即wij=wji。因此此时,网络一定能够收敛到一个稳定值。否则,则网络可能会不稳定,无法收敛。
离散Hopfield网络每个单元均有一个状态值,它取两个可能值之一。
设在某一个时刻t,神经元i的状态为Ui(t),则在t+1时刻的状态为:
(19)
其中,wij为神经元i何j之间的连接权值,i为第i个神经元的阈值。
Hopfield网络算法的流程如下:
(1)设置互联权值
(20)
式中,为S类采样的第i个分量,可为+1或-1;采样类别数为m,节点数为n。
(2)对未知类别的采样初始化
yi(0)=xi
式中,yi(t)为节点i在时刻t的输出;当t=0时,yi(0)就是节点i的初始值,xi为输入采样的第i个分量,也可为+1或-1。
(3)迭代运算
(21)
(4)重复迭代
直至每个输出单元不变为止,即Uj(t+1)=Uj(t)
实验过程与结果分析
3.1 实验环境
Windows 10专业版,64位,CPU i5-3.3GHz,内存8G
Matlab R2012a
3.2实验数据集
MNIST数据集是一个被广泛用于训练各种图像处理系统的大型手写数字数据库,同时,该数据库也常用于人工智能、机器学习、数据挖掘等领域,对分类、聚类和回归模型进行训练,并测试模型的准确性。
MNIST数据集包含60000个训练样本和10000个测试样本,每个样本都是一个28*28像素的BMP图片。因为每一个样本都具有类标签,所以该数据集既可以用于有监督的学习和无监督的学习,并可以使用其类标签来计算模型的准确度。现在,已经有许多学者使用该数据集进行实验,并试图使他们的算法在该数据集上表现出更低的错误率。到目前为止,KNN算法、支持向量机、神经网络、决策树算法已经在该数据集上真实实验过,表现出不同的计算性能。据统计,一种基于DropConnect方法的神经网络在MNIST数据集的实验上能够达到0.21%的错误率,是至今为止分类效果最好的。
3.3数据预处理
MNIST数据集是NIST的一个子集,一共包含四个文。MNIST数据的原始数据为Ubyte文件,上述四个文件中,train-images,和train-labels用来训练模型 ,t10k-images和t10k-labels用来评估所训练模型的准确性。如图所示,Matlab无法直接处理该数据集,因此需要对数据集进行预处理。
图3-1 MNIST数据集的原始文件
将Ubyte文件转换成.mat文件的主要过程分为两步,
第一步:将Ubyte文件转换为BMP图片格式。源代码如下:
%读取训练图片数据文件
[FileName,PathName] = uigetfile('*.*','选择测试图片数据文件t10k-images.idx3-ubyte');
TrainFile = fullfile(PathName,FileName);
fid = fopen(TrainFile,'r');
a = fread(fid,16,'uint8');
MagicNum = ((a(1)*256+a(2))*256+a(3))*256+a(4);
ImageNum = ((a(5)*256+a(6))*256+a(7))*256+a(8);
ImageRow = ((a(9)*256+a(10))*256+a(11))*256+a(12);
ImageCol = ((a(13)*256+a(14))*256+a(15))*256+a(16);
%提取Ubyte数据集的相关参数
savedirectory = uigetdir('','选择测试图片路径:');
h_w = waitbar(0,'请稍候,处理中>>');
for i=1:ImageNum
b = fread(fid,ImageRow*ImageCol,'uint8');
c = reshape(b,[ImageRow ImageCol]);
d = c';
e = 255-d;
e = uint8(e);
savepath = fullfile(savedirectory,['TestImage_' num2str(i,'%05d') '.bmp']);
imwrite(e,savepath,'bmp');
waitbar(i/ImageNum);
end
fclose(fid);
close(h_w);
第二步:将BMP图片转换为.mat文件,保存在Matlab的工作空间。
预处理之后的数据集格式如下:
TrainItem.mat 60000*784
TestItem.mat 10000*784
TrainLable.mat 60000*1
TestLable.mat 10000*1图3-2 预处理之后的数据集
3.4决策树分类实验
3.4.1实验过程
Step1:导入实验数据集
load(‘TestItem.mat’);
load(‘TestLable.mat’);
load(‘TrainItem.mat’);
load(‘TrainLable.mat’);
Step2:使用训练数据集及其标签集训练模型,得到决策树,并输出,如图3-3所示
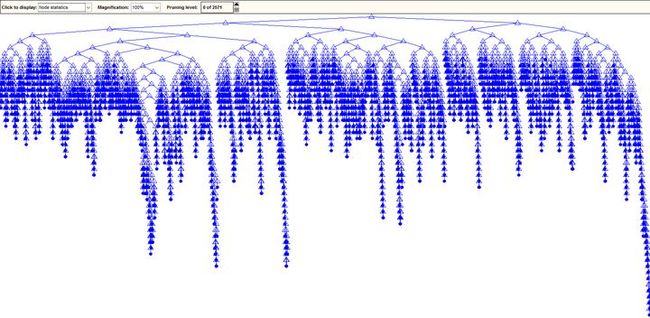
Tree=classregtree(TrainItem,TrainLable);
图3-3 决策树模型
Step3:使用训练好的决策树对测试集进行分类,并得到分类结果
value_table=round(eval(Tree,TestItem));
Step4:将分类得到的数据类标签与已知的类标签进行比较,画出预测类标签与实际类标签的对比图,计算得到决策树的准确率。
count=0;
for i=1:1:10000
if TestLable(i)==value_table(i)
count=count+1;
end
end
precision=count/10000
3.4.2实验结果
本实验另外又将实验数据进行归一化处理,按照上述实验过程进行相同的实验,现将实验结果整理如表3-1所示:
表3-1 决策树实验结果
| 准确率 | 计算时间(s) | |
| 无归一化处理 | 0.8352 | 110.68 |
| 归一化处理 | 0.8353 | 108.25 |
通过观察发现,归一化处理对决策树的分类效果影响不大。
在Step4中画出的测试集的预测类标签与实际类标签的对比图如图4-4所示,其中,两种标记为重叠的部分即为预测失误的数据。
图3-4 决策树预测类别与实际类别的对比
3.5 SVM分类实验
3.5.1实验过程
Matlab R2012a自带的SVM工具箱只能对数据进行二分类,实验结果并不理想,因此需要预先加载libSVM工具箱,对SVM的实验性能进行验证。
Step1:导入实验数据集
load(‘TestItem.mat’);
load(‘TestLable.mat’);
load(‘TrainItem.mat’);
load(‘TrainLable.mat’);
Step2:对训练数据集及测试数据集进行归一化,将数据映射到[0,1]区间,这里使用的方法是将每一项数据除以最大值255,也可以使用Matlab自带的归一化函数mapminmax(),效果一样。
TrainItem=TrainItem/255;
TestItem=TestItem/255;
Step3:利用训练集及其类标签建立分类模型,并输出分类模型的相关参数。
%训练模型
model = svmtrain(trainlabel,traindata);
%输出模型参数
model
Parameters = model.Parameters
Label = model.Label
nr_class = model.nr_class
totalSV = model.totalSV
nSV = model.nSV
Step4:使用训练好的模型对测试集进行分类,并得到SVM的准确率。
[PredictLable,Acc,Toss] = svmpredict(testlabel,testdata,model);
TestAccuracy=Acc(1);
3.5.2实验结果
实验开始阶段并未对训练数据集和测试数据集进行归一化处理,使用训练好的SVM模型对测试数据集进行分类得到的准确率为TestAccuracy=11.35%。这个结果与预期的结果相差甚远,与查阅的相关资料上提到的SVM的准确率也有较大的出入。仔细检查了各项相关输出之后发现,预测类标签的输出PredictLable表中的数据全部为1,即将测试数据集的每一个实例的类别均预测为1,恰好是10%的准确率。因此猜想可能是未对数据集进行归一化处理,导致各个数据之间的差距较大,影响了模型的准确性。
对数据进行归一化处理后,随机抽取不同数目的训练集数据对模型进行训练,实验结果如表3-2所示:
表3-2 SVM实验结果
| 训练数据集数目 | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 |
| 准确率 | 92.22% | 93.25% | 93.74% | 94.03% | 94.32% | 94.53% |
| 计算时间(s) | 175.05 | 458.22 | 810.40 | 1325.24 | 1869.79 | 2470.15 |
实验结果表明,随着使用的训练数据集样本数目的增多,SVM训练模型的准确率逐渐升高,对测试数据的预测效果越好,没有出现过拟合现象。在时间开销上,其增长速率要高于准确率的增长速度,但是在可接受的范围内。
3.6人工神经网络分类实验
3.6.1实验过程
Step1:导入实验数据集。因为神经网络模型对数据进行处理时是以一列为一个数据实例的。
load(‘TestItem.mat’);
load(‘TestLable.mat’);
load(‘TrainItem.mat’);
load(‘TrainLable.mat’);
Step2:在命令行窗口输入nntool,打开神经网络工具箱的操作界面。
图3-5 神经网络界面
Step3:点击Import,将输入数据和输出数据导入工作空间。
图3-6 导入数据
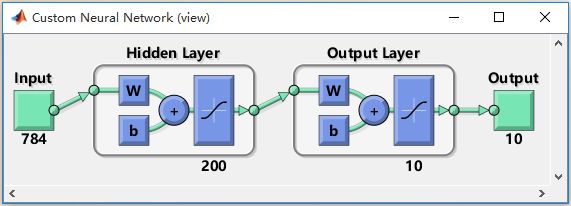
Step4:点击New按钮,创建一个新的神经网络,并设置它的名称、类型、输入输出及隐层神经元的个数等参数。确认无误后点击Create按钮,神经网络创建成功。创建好的神经网络抽象模型如下图所示:
图3-7 神经网络模型
Step5:导入训练数据集及训练数据标签,点击Train按钮使用训练样本对神经网络模型进行训练,训练过程的相关参数如下图:
图3-8 模型参数
Step6:模型训练完成之后,点击Simulate按钮对测试数据集进行分类,将分类结果和实验误差输出。
3.6.2实验结果
实验过程中,将数据集的类标签用两种形式表示,例如类标签3有两种表示形式,第一种为10位表示t=[0001000000];第二种为1位表示t=[3],两种表示形势下分别进行实验,结果有很大的不同,现将实验结果表示如下。
(1)类标签表示为10位
a. Performance
神经网络模型训练过程中将训练数据集分为三部分:训练数据集Train,验证数据集Validation,测试数据集Test。为了防止过拟合现象的发生,一般将Validation数据集分类效果最好时训练好的模型进行输出,如图4-9所示,在第153次迭代时,神经网络模型的效果达到最好。
图3-9 性能
b. Training State
图3-10显示了神经网络模型训练过程的相关状态,在第153次迭代时,神经网络梯度为0.0010172,交叉验证的次数为6次。该数据表示在神经网络利用训练数据集进行训练的过程中,验证数据集的误差曲线连续6次迭代不再下降。如果随着网络的训练,验证数据集的误差已经不再减小,甚至增大,那么就没有必要再去训练网络了,因为继续训练下去的话,再利用测试测试集对模型进行测试的话,测试数据集的误差将同样不会有所改善,甚至会出现过度拟合的现象。
图3-10 训练状态
c. Regression
图3-11 回归曲线
d. Precision
Precision=0.9969
(2)类标签表示为1位
a. Performance
图3-12显示,当使用一位数据表示类标签是,在第257次迭代神经网络模型的效果达到最好。
图3-12 性能
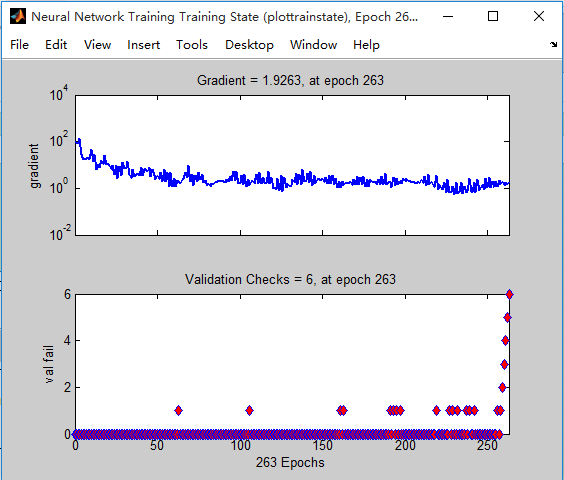
b. Training State
图3-13显示了神经网络模型训练过程的相关状态,在第263次迭代时,神经网络梯度为1.9263,交叉验证的次数为6次。
图3-13 训练状态
c. Regression
图3-14回归曲线
d. Precision
Precision=0.6024
结论
此次实验利用Matlab工具箱对三种分类算法:决策树算法、SVM算法和神经网络算法进行实现,通过对MNIST数据集进行分类,并且使用其真实数据标签与预测标签进行比较,能够得到各个分类算法的准确率。通过比较发现,三种分类算法在算法的执行速度以及分类的准确率方面表现出了显著地差异。
4.1 三种分类算法的比较
决策树算法、SVM算法以及神经网络算法在MNIST数据集上的执行速度以及分类的准确率如表4-1所示,表中所列数据为每个算法最佳参数下十次重复实验数据的平均值。
表4-1 三种分类算法的性能比较
| 指标 | 决策树算法 | SVM算法 | 神经网络算法 |
| 准确率 | 83.53% | 94.53% | 99.69% |
| 执行时间(s) | 108.25 | 2470.15 | 512 |
通过分析表4-1可以得出以下结论:
(1)在分类的准确率方面,神经网络的准确率最高,SVM算法次之,决策树算法的准确率最低。
(2)在算法的执行速度方面,决策树算法的的运行速度最快,神将网络算法的运行速度较慢,SVM算法的运行速度最慢。
(3)对MNIST数据集的分类而言,综合考虑应该选择神经网络算法,因为该算法分类的准确率几乎达到100%,而执行速度相对来说不是最慢的,在可接受的范围内。
4.2 决策树算法的分析
通过分析表4-2所示的决策树的实验结果可知,决策树分类算法的速度之快是其最显著的特点。另外,虽然MNIST数据集中的数值分布较为分散,数值之间的差异较大,但是这对决策树算法的准确率并没有影响,因此可以看出,决策树算法对于实验数据的分布均匀与否并不敏感。
表4-2 决策树算法的实验结果
| 准确率 | 计算时间(s) | |
| 无归一化处理 | 0.8352 | 110.68 |
| 归一化处理 | 0.8353 | 108.25 |
4.3 SVM算法分析
在对SVM算法进行实验时,对其进行了两方面实验:一方面探究了数据的归一化对算法准确率的影响。另一方面则探究了训练数据集的大小对分类准确率的影响。
实验结果表明:
(1)未对数据进行归一化时,算法的准确率为11.35%,将全部数据的类别预测为1;对数据进行归一化之后,算法的准确率达到94.53%。因此,可以得出结论:SVM算法对于分布不均的数据集是较敏感的。
(2)随着训练数据集样本数目的增加,算法的准确率越来越大,算法执行时间越来越长,如表4-3所示。因此可以得出结论:使用SVM算法对MNIST数据集进行分类时,使用的训练数据集的样本越多,分类效果越好。
表4-3 SVM算法实验结果
| 训练数据集样本数目 | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 |
| 准确率 | 92.22% | 93.25% | 93.74% | 94.03% | 94.32% | 94.53% |
| 计算时间(s) | 175.05 | 458.22 | 810.40 | 1325.24 | 1869.79 | 2470.15 |
4.4 神经网络算法分析
在对神经网络算法进行实验时,对其进行了两方面实验:一方面探究了数据的归一化对算法准确率的影响。另一方面则探究了数据类标签的表示位数对分类准确率的影响。
实验结果表明:
(1)未对数据进行归一化时,算法的准确率为82.11%;对数据进行归一化之后,算法的准确率达到99.69%。因此,可以得出结论:MNIST数据集的归一化与对神经网络算法的精确率有一定的影响,但相比于SVM算法来说,影响不大。
(2)使用一位数据表示数据类标签时,神经网络算法的准确率为60.24%,使用十位数据表示数据类标签(即第几位为1表示数据被预测为第几类)时,神经网络算法的准确率为99.69%,因此可以得出的结论为:神经网络算法的准确率与构建模型时数据类标签的表示位数有较大的关系。
参考文献
[1] 数据挖掘: 概念与技术[M]. 机械工业出版社, 2007
[2] Quinlan J R. Induction of decision trees[J]. Machine learning, 1986, 1(1): 81-106.
[3] Quinlan J R.C4.5: programs for machine learning[M].Morgan Kaufmann,1993:23-30
[4] Niuniu X, Yuxun L. Review of decision trees[C]//Computer science and information technology (ICCSIT), 2010 3rd IEEE International Conference. 2010: 105-109.
[5] BOSER B E,GUYON I M,VAPNIK V N. A training algorithm for optimal margin classifiers[C]//Proceedings of The Fifth Annual Workshop on Computational Learning Theory. New York: ACM Press, 1992: 144-152.
[6] SYED N, LIU H, SUNG K. Incremental learning with support vector machines[C]//International Joint Conference on Artificial Intelligence. Sweden: Morgan kaufmann publishers, 1999: 352-356
[7] GAUWENBERGHS G, POGGIO T. Incremental and decremented support vector machine[J]. Machine Learning.2001, 44 (13): 409- 415.
[8] RALAIVOLA L, FLORENCE D’ALCHÉ-BUC. Incremental support vector machine learning: a local approach[C]//Proceedings of International Conference on Neural Networks. Vienna, Austria: [J], 2001:322-330.