机器学习实战 2.4从数据探索和可视化中获得洞见
创建一个副本不伤害原始数据集。为了接下来能顺利使用plt函数,import新的库:
housing = strat_train_set.copy()
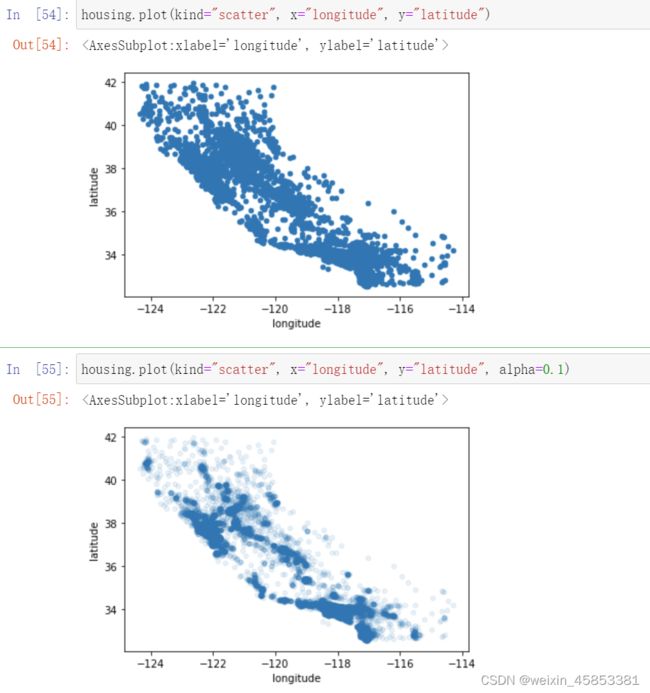
import matplotlib.pyplot as plt;2.4.1 将地理数据可视化
将 alpha 设置为0.1,显示高密度点的位置:湾区、洛杉矶、圣地亚哥。
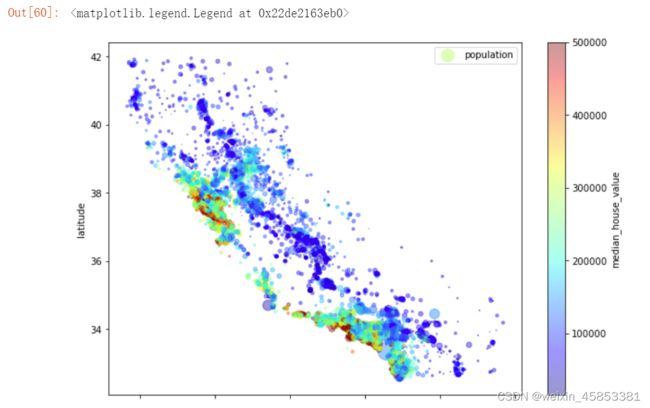
为了更加图像能够凸显更多的信息,将每个区域的人口数量作为图中每个圆的半径大小,房价中位数表示圆的颜色,使用预定义颜色表 "jet"(选项cmap) ,颜色由(低房价)到红(高房价)。
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
)
plt.legend()2.4.2 寻找相关性
使用 corr() 方法计算每对属性之间的皮尔逊相关系数r。相关系数范围 [-1, 1] ,越接近 1 表示有越强的正相关,越接近 -1 表示有越强的负相关。
注意:这里只能测量出是否线性相关。
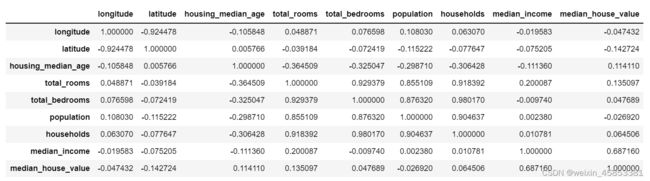
corr_matrix = housing.corr()
corr_matrix 现在看每个属性与房价中位数的相关性是多少:
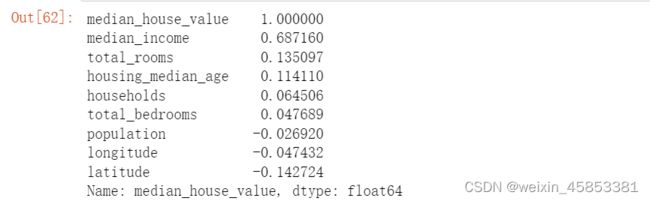
corr_matrix["median_house_value"].sort_values(ascending=False)收入与房价是最正相关的,纬度和房价最负相关(越往北房价越低)。
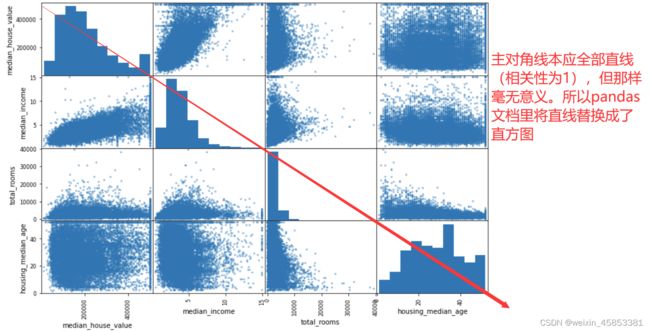
还有一种检测相关性的方法:使用 pandas 的 scatter_matrix 函数。他会绘制出每个数值属性相对于其他数值属性的相关性。比如现在有 11个数值属性,能够得到 11*11=121个图像。这里我们选取与房价中位数最相关的(潜力)属性。
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
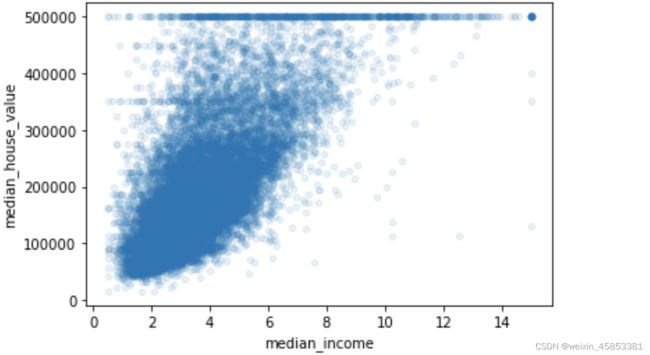
scatter_matrix(housing[attributes], figsize=(12, 8))与房价中位数最相关的属性是收入中位数,我们将上图中的收入中位数散点图单独拿出来:
2.4.3 试验不同属性的组合
在把训练集投入模型之前,我们应该尝试各种属性的组合,来将不同的、目前单看没有什么意义的属性组合成一个更有用的属性。例如,相比于一个区域的房间总数 (total_rooms) 与家庭数量 (households) ,我们可能更需要的是单个家庭的房间数量 (rooms_per_household) 。
我们尝试创建一些新属性:
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"] #总房间数/户数=每户拥有的房间数
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]#总卧室数/总房间数=卧室占比
housing["population_per_household"]=housing["population"]/housing["households"]#人口/户数=每户人数再看看新的相关性矩阵:
# 计算相关矩阵
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)可以看出,新的三个属性相关性都是挺高的!
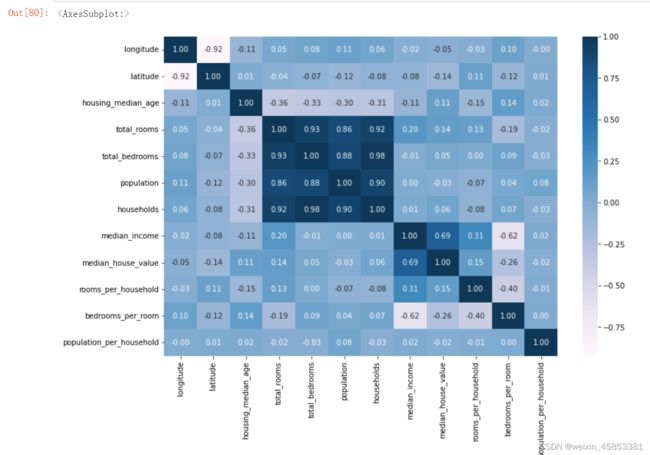
最后,做一个目前为止的相关性热图:
import seaborn as sns
plt.figure(figsize=(12,8))
sns.heatmap(housing.corr(), annot=True, fmt='.2f', cmap='PuBu')