数字图像学习笔记(一)——灰度变换
基本灰度变换函数
1 对数变换
s = c ∗ l o g ( 1 + v ⋅ r ) s=c*log(1+v·r) s=c∗log(1+v⋅r)
-
输出灰度级 s s s
-
常数 c c c
-
输入灰度级 r ( r ≥ 0 ) r(r≥0) r(r≥0)
-
底数一般为 v + 1 v+1 v+1
MATLAB 对数变换函数效果代码:
f = 0:0.01:1;
v1 = 1;
y1 = log2(1 + v1*f)/log2(v1+1);
v2 = 10;
y2 = log2(1 + v2*f)/log2(v2+1);
v3 = 50;
y3 = log2(1 + v3*f)/log2(v3+1);
v4 = 100;
y4 = log2(1 + v4*f)/log2(v4+1);
v5 = 200;
y5 = log2(1 + v5*f)/log2(v5+1);
plot(f,y1,'green',f,y2,'red',f,y3,'blue',f,y4,'yellow',f,y5,'black');
xlabel('Input gray level');
ylabel('Output gray level');
title('Log transformation: g = log(1+v*r)/log(1+v)');
lgd = legend('Log(v=1)','Log(v=10)','Log(v=50)','Log(v=100)','Log(v=200)');
legend('Location','southeast');
title(lgd,'The logarithmic function of gray transformation')
得出图像:

则我们可以得出:
-
对数变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度级。
即低灰度值部分扩展,高灰度值部分压缩
-
起到了暗处亮度增大的作用,而原本的亮处变化不明显
-
同理可推,反对数变换则是亮处亮度减小,原来的暗处变化不明显
以本人女神刘亦菲举例(不是)
举例:
f = imread('E:\Matlab Experiment\Liuyifei.jpg'); % 读取图像函数
% 对数变换
c = 1;
g = c* log(1 + double(f)); % c是一个常数
gs = im2uint8(mat2gray(g)); % 使用函数 mat2gray 可将值限定在范围 【0,1】内,使用 im2uint8 可将值限定在【0,255】内
imshow(gs)
则输入输出图像如下所示(暗处变亮)

2 幂律(伽马)变换
s = c r γ s=cr^γ s=crγ
MATLAB 幂律(伽马)变换函数效果代码:
f = 0:0.001:1;
v1 = 1;
y1 = v1*(f.^0.1);
y2 = v1*(f.^0.2);
y3 = v1*(f.^0.5);
y4 = v1*(f.^1);
y5 = v1*(f.^2);
y6 = v1*(f.^10);
y7 = v1*(f.^25);
plot( f, y1, 'red', f, y2, 'green', f, y3, 'blue', f, y4, 'black', f, y5, 'blue', f, y6, 'green', f, y7, 'red');
xlabel('Input gray level');
ylabel('Output gray level');
title('Exponential transformation: s = c*r^γ');
lgd = legend('y1','y2','y3','y4','y5','y6');
legend('Location','southeast');
title(lgd,'relation')
得出图像:

则我们可以得出:
- 幂律曲线用分数值 γ γ γ 将较窄范围的暗输入值映射为较宽范围的输出值,将高输入值映射为较窄范围的输出值
- 改变 γ γ γ 的值能得到一族变换曲线
- c = γ = 1 c = γ = 1 c=γ=1 时,称为恒等变换
- γ γ γ 大于 1 1 1 与小于 1 1 1 产生的效果是相反的
- 约定:幂律公式中的指数称为 伽马校正 或 伽马编码
- 可使用幂律变换来增强(减小)对比度
举个例子:
clc;
clear;
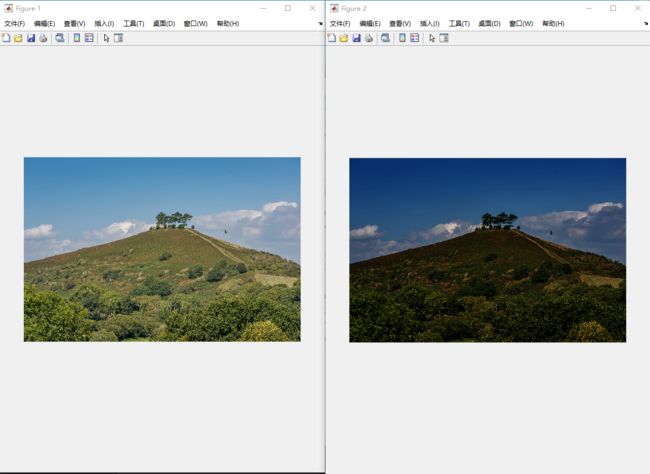
f = imread('E:\Matlab Experiment\hill.jpg'); %读取图像函数
imshow(f)
figure
%幂律变换
c = 1;
g = c*(double(f).^2.5);
% g = c* log(1 + double(f));
gs = im2uint8(mat2gray(g));
imshow(gs)
图像输入输出如下:
3 分段线性变换函数
3.1 对比度拉伸
典型变换来解释:

点 ( r 1 , s 1 ) (r_1,s_1) (r1,s1) 和点 ( r 2 , s 2 ) (r_2,s_2) (r2,s2) 的位置控制变换函数的形状。
一般假设 r 1 ≤ r 2 r_1≤r_2 r1≤r2 且 s 1 ≤ s 2 s_1≤s_2 s1≤s2 ,以便于保证函数是单值且单调递增的。这样会保留灰度级的顺序,防止产生灰度伪影。
-
r 1 = s 1 , r 2 = s 2 r_1=s_1,r_2=s_2 r1=s1,r2=s2 ,那么变换就是一个不改变灰度的线性函数

-
r 1 = r 2 , s 1 = 0 , s 2 = L − 1 r_1=r_2,s_1=0,s_2=L-1 r1=r2,s1=0,s2=L−1,那么变换成为创建以复二值图像的阈值处理函数

MATLAB程序实例:
clc;
clear;
f = imread('E:\Matlab Experiment\hill.jpg'); %读取图像函数
imshow(f)
figure
%灰度阈值变换
level = 0.5 %范围为【0,1】
g = im2bw(f, level);
% g = imbinarize(f, level);
gs = im2uint8(mat2gray(g));
imshow(gs)
3.2 灰度级分层
- a a a 图突出了区间 [ A , B ] [A,B] [A,B] 内的灰度,而将其他灰度降低了一级
- b b b 图突出了区间 [ A , B ] [A,B] [A,B] 内的灰度,而保持其他灰度级不变
3.3 比特平面分层
像素值是由比特值组成的整数,256级灰度图像中图像值是由 8 比特(1 字节)组成的
如上图所示,8 比特图像可视为由 8 个 1 比特平面组成,其中平面 1 包含图像中所有像素的最低有效比特,而平面 8 包含图像中所有像素的最高有效比特。
每一个比特图像都是一幅二值图像。将所有像素的相同比特位的数字拿出来组成一个矩阵,就会有 8 个矩阵。 以一个 3 比特的 3*3 大小的矩阵为例。
-
将各像素位置处的灰度值转换成二进制,如下图
( 7 2 4 4 6 3 2 5 2 ) → ( 111 010 100 100 110 011 010 101 010 ) \begin{pmatrix}7 & 2 & 4 \\ 4 & 6 & 3\\ 2 & 5 & 2 \end{pmatrix}\rightarrow\begin{pmatrix}111 & 010 & 100 \\ 100 & 110 & 011\\ 010 & 101 & 010 \end{pmatrix} ⎝⎛742265432⎠⎞→⎝⎛111100010010110101100011010⎠⎞ -
将各相应位置处的数取出组成矩阵,从左到右分别是比特平面3、2、1
( 1 0 1 1 1 0 0 1 0 ) ( 1 1 0 0 1 1 1 0 1 ) ( 1 0 0 0 0 1 0 1 0 ) \begin{pmatrix}1 & 0 & 1 \\ 1 & 1 & 0\\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix}1 & 1 & 0 \\ 0 & 1 & 1\\ 1 & 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 & 0 \\ 0 & 0 & 1\\ 0 & 1 & 0 \end{pmatrix} ⎝⎛110011100⎠⎞⎝⎛101110011⎠⎞⎝⎛100001010⎠⎞
如下图实例,a为原图,b ~ i 为比特平面 8 到比特平面 1
由图可见高比特平面较低比特平面所含信息量要大



