CTR深度学习模型之 DeepFM 模型解读

CTR 系列文章：

1. 广告点击率(CTR)预测经典模型 GBDT + LR 理解与实践（附数据 + 代码）
2. CTR经典模型串讲：FM / FFM / 双线性 FFM 相关推导与理解
3. CTR深度学习模型之 DeepFM 模型解读
4. 【CTR模型】TensorFlow2.0 的 DeepFM 实现与实战(附代码+数据)
5. CTR 模型之 Deep & Cross (DCN) 与 xDeepFM 解读
6. 【CTR模型】TensorFlow2.0 的 DCN(Deep & Cross Network) 实现与实战(附代码+数据)
7. 【CTR模型】TensorFlow2.0 的 xDeepFM 实现与实战(附代码+数据)

上一篇文章讲了一些比较经典的 CTR 模型：CTR经典模型串讲：FM / FFM / 双线性 FFM 相关推导与理解，从这一篇文章开始将会陆续介绍一些使用深度学习完成CTR预估的模型，本文主要讲的是DeepFM模型。

之前讲的 FM、FFM、Bi-FFM 本质上都是要学习户点击行为背后隐含的特征组合，不过这些经典模型主要是进行二阶特征组合。理论上也可以进行更高阶的特征组合，但是会造成特征维度指数级增长以及数据稀疏等问题。对于高阶特征组合问题不难想到可以用多层的神经网络解决。

DeepFM 的整体结构

对于类别变量，需要进行onehot编码后输入到DNN中，但是常规的做法会导致网络参数过多：

为了减少参数数量，可以借鉴FFM的思想，将特征划分为不同的 field：

然后再接上几个全连接层完成高阶特征组合：

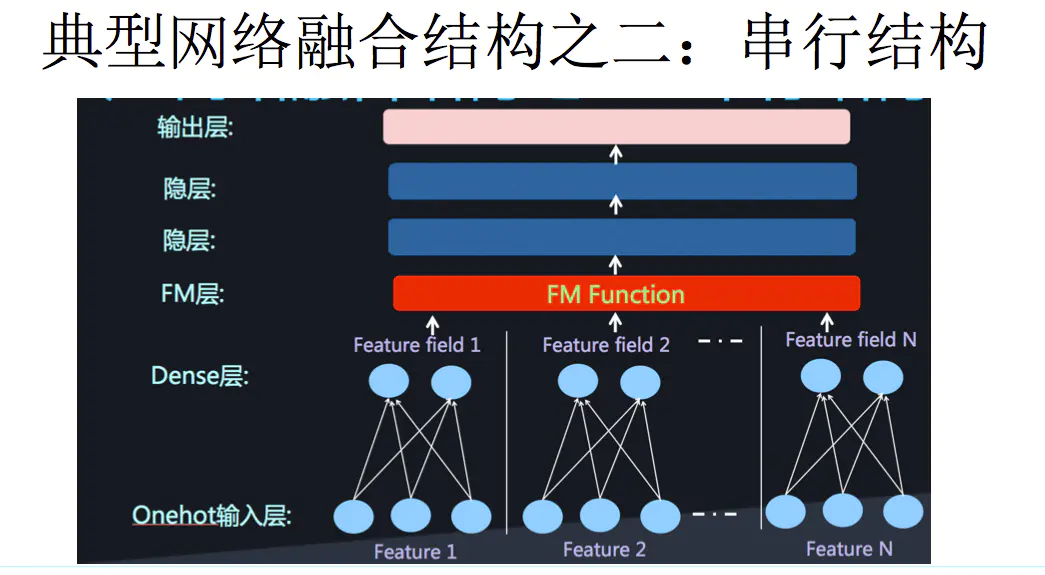
当然，我们也可以单独进行低阶特征组合，然后和高级特征融合，即将DNN与FM进行融合。具体的形式有两种，一是串行结构，二是并行结构：

DeepFM 是并行结构的代表，具体结构如下：

此模型主要分为左边的FM模块与右边的DNN模块，最终的预测由两部分的输出相加得到：
$$\hat{y}=sigmoid(y_{FM}+y_{DNN})$$

DeepFM 中的 FM 模块

FM模块如下图所示：

此部分实现的功能是：
$$y_{FM}=⟨w,x⟩+\sum _{i=1}^d\sum _{j=i+1}^d⟨V_i,V_j⟩x_i\cdot x_j$$
首先看看式子的第一项 $<w,x>$ 的计算是由下图中黄色实心圆表示的每个field的非零值相以及绿色箭头都代表的权重 w 相乘后累加而得。

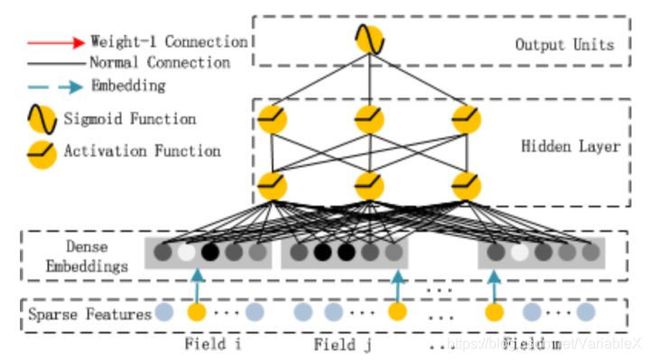
接下来介绍FM式子中的二次项计算过程。首先理解下图中的 Dense Embeddings 层，如果对输入层和embedding层展开后可以得到下面的图：

看到图中的 $V_{11},V_{12},V_{ik}$是不是很熟悉？由于CTR的输入层一般是很稀疏的向量，因此需要隐藏层之前，先按照不同的 field 进行 embedding 操作将高维稀疏压缩向量到低维稠密向量。这个 embedding 过程有两个特点：

1，不同的 field 的输入可能不同，但是在embedding之后向量的长度均为K

2，在 FM 里得到的隐变量 $V_{ik}$ 现在作为了嵌入层网络的权重

举个例子，假设 embedding 后的维度 k=5，则对于每个 field 的输入，只有一个输入节点 $x_i$ 为1，例如 $x_2=1$，此时输入层与对应的 filed 层中，仅有五条带有权重的线与 embedding 层相连，这五条线上的权重 $V_{21},V_{22},V_{23},V_{24},V_{25}$ 的组合即为 FM 公式第二项中的 $V_2$，如下图绿色箭头所示：

同理，我们可以得到 $V_1,V_3....V_n$，然后在 FM 层中对不同 $V_i,V_j$的组合进行内积计算，例如下图中绿色箭头所示：

最后，在最上层使用 sigmoid 激活函数得到该 FM 模块的输出值。

DeepFM 中的 DNN 模块

首先看看这个模块的整体结构：

此模块使用多层前馈神经网络，用于学习高阶交叉特征。具体过程是：得到了 Embedding 层的输出后，连接一些隐藏层，然后在最上面的输出层使用 sigmoid 函数得到最后的输出值。

需要注意的是，隐藏层的输入是 Embedding 层，这个嵌入层是 FM 模块与 DNN 模块所共享的。这带来两个好处：

1，可以从原始特征中学习到低阶和高阶特征

2，不需要专业的特征工程

到此为止，DeepFM 模型相关的解释说明就结束了，后续可能会有文章讲解 tensorflow2 的相关代码实现。

参考文章：

DeepFM技术细节

推荐系统遇上深度学习(三)–DeepFM模型理论和实践