强化学习：确定性策略梯度（DDPG）

1，确定性策略梯度

1.1，基本概念

随机性策略梯度算法被广泛应用于解决大型动作空间或者连续动作空间的强化学习问题。其基本思想是将策略表示成以  为参数的策略函数  。基于采样数据，通过调整参数  使得最终的累计回报最大。即：通过一个概率分布函数  ，来表示每一步的最优策略，在每一步根据该概率分布进行行为采样，获得当前的最佳行为取值；生成行为过程，本质上是一个随机过程；最后学习到的策略也是一个随机策略。

使用确定性策略的主要原因是随机策略梯度方法有以下缺陷：

• 即使通过随机策略梯度学习到了随机策略，在每一步行为时，还需要对得到的最优策略概率分布进行采样，才能获得行为的具体值；而行为通常是高维的向量，如20维，50维，在高维的行为空间频繁采样，是很耗费计算能力的。
• 在随机策略梯度的学习过程中，每一步计算策略梯度都需要在整个行为空间进行积分，同样很耗费计算能力。

由于公式可见其是关于状态和动作的期望，在求期望时，需要对状态分布和动作分布进行积分。这就要求在状态空间和动作空间采集大量的样本，这样得到的均值才能近似期望。

而确定性策略的动作是确定的，所以在确定性策略梯度存在的情况下，对确定性策略梯度的求解不需要在动作空间进行采样积分。因此，相比于随机策略方法，确定性策略需要的样本数据要小，确定性策略方法的效率比随机策略的效率高很多，这也是确定性策略方法的主要优点。

1.2，确定性策略梯度定理

整个确定性策略梯度方法沿用了行动者-评论家学习框架，评论家（Critie）使用可微近似函数估计行为值函数，行动者（Actor）朝着行为值函数梯度方向更新策略参数。在引入AC框架之前，大多数无模型强化学习算法都是基于广义策略迭代框架，将策略评估与策略改进相结合求解最优值。其中，策略评估方法通过蒙特卡罗评估或者时序差分方法学习行为值函数 或  。策略改进方法根据（估计的）行动价值函数更新策略，最常见的方法是使用贪心算法最大化动作值函数  。在连续行为空间场景下，针对每个状态求取最大行为值函数不切实际。很多研究者想到是否可以让策略朝着行为值函数梯度的方向进行更新，这是一个相对简单、计算量相对较小的替代性方案。具体来说，就是针对每个访问状态  ，让策略参数  按比例朝着值函数梯度 方向更新。每个状态  都可以计算出不同的更新量，最终的更新总量就是以状态  的分布  为该类对这些更新量求期望。

应用链式求导法则，策略更新被分解为两部分，第一部分行为值函数对行为的梯度，第二部分为策略相对于策略参数的梯度。

其中， 是一个雅克比矩阵，该矩阵的第  列表示策略的第  个维度相对于策略参数  的梯度  。

理论上认为，当策略改变时，状态分布  也会改变。事实上，在不考虑策略变化对状态分布的影响时，更新策略对结果的影响并不大。正如确定性梯度定理所表明的那样，计算策略梯度时，不需要计算状态分布的梯度。

假设在一个马尔可夫决策过程模型中， ，，，， ，， 分别存在，并且对于  都是连续函数，其中  表示初始状态概率分布， 表示状态转移概率。 以上条件是为了保证  和  存在，那么确定性策略梯度一定存在且满足：

2，DPG算法

2.1，在线策略确定性AC算法

一般来说，通过确定性策略进行采样无法确保充分探索，最终可能导致一个次优解决方案。因此，在线策略确定性行动者-评论家算法仅有理论意义。但是考虑到环境噪声的影响，在某些情况下，即使是采用了确定性策略，但只要环境中存在足够的噪声，也可以确保我们能够对环境进行充分探索。这种情况下，在线策略方法也可以找到最优解。

就像随机的行动者-评论家方法一样，确定性的行动者-评论家方法也由两部分组成。评论家评估动作值函数，而行动家对行为值函数才用梯度上升法更新策略参数。不同的是，行动者更新  的参数  时遵循的是确定性策略梯度定理。

与随机的行动者-评论家方法一样，评论家可以使用可微近似函数  代替真实动作值函数 ，，并通过策略评估方法（如Sarsa）来进行迭代更新得到参数值  。

2.2，离线策略确定性 AC

确定性策略算法在进行强化学习时，存在一个问题：给定状态  和策略参数时，动作是固定的。也就是说，当初始状态确定，通过确定性策略所产生的的轨迹永远都是固定的，智能体无法探索其他的轨迹或访问其他的状态。为了确保在使用确定性策略梯度方法的前提下，依然能够对状态进行充分探索，引入离线学习策略学习方法。即：行动策略是随机策略，评估策略是确定性策略。

离线策略方法使用行为策略  采样生成样本数据，基于样本数据对目标策略  进行改进。目标策略  是确定性策略。对应地，将目标函数修改为目标策略的值函数 基于行为策略  状态分布的积分：

其中， 表示行为策略  下的状态折扣分布。根据确定性策略梯度定理得到离线策略梯度：

同样地，评论家使用可微近似函数  代替真实的动作值函数  ， 。

离线策略确定性行动者-评论家（OPDAC）：评论者使用 Q-learning 来估计和更新值函数。

随机离线策略  算法通常对行动者和评论家都使用了重要性采样，但是，因为确定性策略梯度省去了对动作空间的积分，则避免了在行动者（Actor）中进行重要性采样，并且通过使用  ，避免了评论家（Critic）的重要采用。

3，DDPG算法

3.1，DDPG简介

DQN是第一个将深度学习与强化学习结合在一起的方法，通过将大型神经网络作为函数逼近器，成功地掌握了直接从高维视频像素中学习控制策略的方法。然而，因为DQN在每次迭代中都需要寻找行为值函数的最大值，因此它只能处理离散的、低维的动作空间。针对连续动作空间，DQN没有办法输出每个动作的行为值函数。解决上述连续动作空间问题的一个简单方法是将动作空间离散化，但是动作空间是随着动作的自由度呈现指数增长的。但是，针对大部分任务来说这个方法不现实。而确定性策略梯度法（DPG），可以解决动作空间连续的问题。它通过把策略表示为策略函数 ，将状态  映射为一个确定性的动作。当策略为确定性策略后，使用贝尔曼方程计算行为值函数  的公式，由：

变为：

于是内部期望的求解就被避免，外部期望只需根据环境求期望即可。也就是说动作-状态值函数  只和环境有关系，与求解动作无关。

有了  值，就可以通过下式迭代求解最优策略：

确定性策略梯度（DPG）可以处理连续动作空间的任务，但是无法直接从高维输入中学习策略；而DQN可以直接进行端对端的学习，却仅能处理离散动作空间问题。将两者结合起来，在DPG算法的基础上引入DQN算法的成功经验，就有了深度确定策略梯度算法（DDPG）。DDPG分别用神经网络逼近行为值函数 （Critic网络）和 （Actor网络），实现了直接从原始数据中进行端对端的学习。

3.2，算法要点

因为强化学习的数据存在马尔可夫性，不满足训练神经网络需要样本独立同分布的前提假设，在使用神经网络进行强化学习时，训练过程很不稳定。为了保证学习效果，需要打破训练数据的相关性。DDPG借鉴了DQN的成功经验，使用了经历回放来解决这个问题。在生成样本数据时，DDPG将从环境中探索得到的数据，以一个状态转换序列为单元  ，存放在记忆库  中。记忆库的容量置为某个值，如500万，当记忆库充满数据时，则需要删掉最旧的样本数据，保证记忆库中永远存放着最新的500万个转换序列。每次更新时，行动者和评论家都会从中随机地抽取一部分样本进行优化，来减少一些不稳定性。

进行神经网络训练时，如果使用同一张神经网络来表示目标网络（target network）和当前更新网络（online），学习过程会很不稳定。因为同一个网络参数在频繁地进行梯度更新的同时，还需要被用于计算网络的梯度。DDPG的解决方案是分别为评论家网络  和行动者网络 ，创建两个神经网络的拷贝。即：分别创建两个独立的目标网络  和  。

Actor网络：策略网络：

Critic网络： 网络：

在训练完一个批量（mini-batch）的数据之后，DDPG通过梯度上升/梯度下降算法更新当前（online）网络的参数。然后再通过滑动平均（soft update）方法更新目标（target）网络的参数。滑动平均指的是在进行目标网络参数更新时，不同于 DQN 直接将 Q 网络的参数复制到目标 Q 网络，DDPG遵循的是： ，且 。这就意味着目标网络参数只能缓慢变化，大大提高了学习的稳定性。

其中 0.001 根据历史经验得到

在连续行为空间学习的一个最主要挑战是如何保证有效的探索。DDPG通过给确定性策略  添加噪声  来构建行为策略，行为策略和评估策略不同，可以保证算法高效“探索”。

除此之外，DDPG还使用了一个被称为批量标准化（BN）的深度学习技术来应对不同量纲问题。比如，位置及速度，显然不能将它们当成一种数据进行处理。因为不同量纲难以找到在具有不同的状态值尺度的环境中泛化的超参数，可能导致网络难以有效学习。批量标准化技术能够对小批量样本中的每个维度进行归一化，以得到单位均值和方差。在探索和评估期间，保持均值和方差平均值用来对得到的数据进行处理，实现不同任务、不同类型的数据进行有效学习。

3.3，算法流程

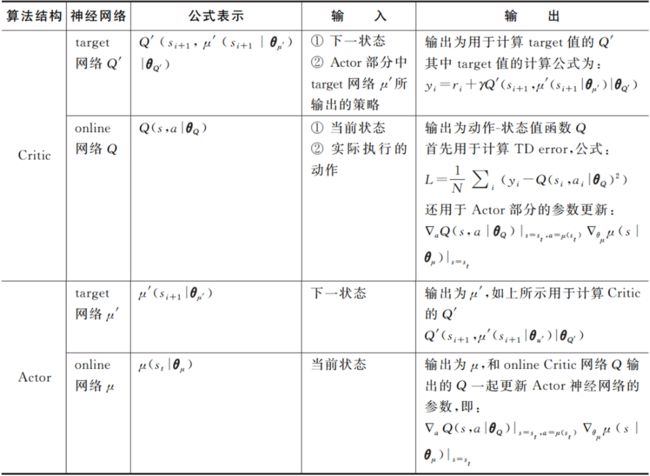
因为采用行动者-评论家架构，所以DDPG有行动者（Actor）和评论家（Critic）两个部分。目标网络和当前更新的网络是两个独立的网络，整个DDPG一共涉及四个神经网络：

• Critic目标网络（target）
• Critic 当前网络（online）
• Actor 目标网络（target） 
• Actor 当前网络（online） 

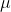
Critic 网络（online）Q 对参数  的更新，采用 DQN 中的 TD error 方式，损失函数为最小化均方差：

其中， ， 的计算用到了目标 Critic 网络  和目标Actor 网络 ，这样做是为了  网络参数的学习过程更加稳定，易于收敛。有了损失函数 ，就可以基于标准的后向传播方法，求得  针对  的梯度  。对其进行优化更新，得到  。

Actor 网络（online） 的网络参数  的更新，遵循确定性策略，公式为（详细请看确定性策略梯度定理的证明）：

 

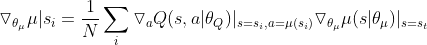
目标网络（target） 和  采用滑动平均方式：

• target Actor 网络  ，其输入为下一状态 ，在计算目标 Critic 的值  时， 用于预测下一状态的行为取值。
• online Actor 网络  ，输入当前状态，输出为当前状态的行为取值。它和 online 的 Critic 一起更新 Actor 神经网络的参数，即：

• target Critic 网络  ，输入为下一状态  和 Actor target 网络中输出的策略  ，输出用于计算 TD 目标，即：

• online Critic 网络  ，输出为当前状态  和实际执行的动作  ，其输出首先用于计算损失函数，公式为 。还用于 Actor 部分的参数更新，即：

具体流程：

DDPG算法吸收了DQN的改进方案，使得算法的效率和效果都得到了保障。比如，通过，通过使用经验库，降低了采样数据的相关性。算法执行过程中，用到了两套 AC 网络，因为 很小，所以目标网络通过滑动平均缓慢更新，使得学习过程更加稳定。

3.4，算法实现（连续动作空间）

以倒立摆作为环境：

import random
import gym
import numpy as np
import torch
from torch import nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
        self.action_bound = action_bound  # action_bound是环境可以接受的动作最大值

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return torch.tanh(self.fc2(x)) * self.action_bound
class QValueNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x, a):
        cat = torch.cat([x, a], dim=1)  # 拼接状态和动作
        x = F.relu(self.fc1(cat))
        return self.fc2(x)
class TwoLayerFC(torch.nn.Module):
    # 这是一个简单的两层神经网络
    def __init__(self,num_in,num_out,hidden_dim,activation=F.relu,out_fn=lambda x: x):
        super().__init__()
        self.fc1 = nn.Linear(num_in, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, num_out)

        self.activation = activation
        self.out_fn = out_fn

    def forward(self, x):
        x = self.activation(self.fc1(x))
        x = self.activation(self.fc2(x))
        x = self.out_fn(self.fc3(x))
        return x

对于策略网络和价值网络，都采用只有一层隐藏层的神经网络，策略网络的输出层用正切函数（y=tanhx）作为激活函数，这是因为正切函数的值域是 ，方便按比例调整成环境可以接受的动作范围。在DDPG中处理的是与连续动作交互的环境，Q网络的输入是状态和动作拼接后的向量，Q网络的输出是一个值，表示该动作对的价值。

def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

class DDPG:
    ''' DDPG算法 '''
    def __init__(self, num_in_actor, num_out_actor, num_in_critic, hidden_dim, discrete, action_bound, sigma, actor_lr, critic_lr, tau,gamma, device):
        # self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        # self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        # self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        # self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        out_fn = (lambda x: x) if discrete else (lambda x: torch.tanh(x) * action_bound)
        self.actor = TwoLayerFC(num_in_actor,num_out_actor,hidden_dim,activation=F.relu,out_fn=out_fn).to(device)
        self.target_actor = TwoLayerFC(num_in_actor, num_out_actor,hidden_dim,activation=F.relu,out_fn=out_fn).to(device)
        self.critic = TwoLayerFC(num_in_critic, 1, hidden_dim).to(device)
        self.target_critic = TwoLayerFC(num_in_critic, 1, hidden_dim).to(device)
        # 初始化目标价值网络并设置和价值网络相同的参数
        self.target_critic.load_state_dict(self.critic.state_dict())
        # 初始化目标策略网络并设置和策略相同的参数
        self.target_actor.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),lr=critic_lr)

        self.gamma = gamma
        self.sigma = sigma  # 高斯噪声的标准差,均值直接设为0
        self.action_bound = action_bound  # action_bound是环境可以接受的动作最大值
        self.tau = tau  # 目标网络软更新参数
        self.action_dim = num_out_actor
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        action = self.actor(state).item()
        # 给动作添加噪声，增加探索
        action = action + self.sigma * np.random.randn(self.action_dim)
        return action

    def soft_update(self, net, target_net):
        for param_target, param in zip(target_net.parameters(),net.parameters()):
            param_target.data.copy_(param_target.data * (1.0 - self.tau) +param.data * self.tau)

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions'],dtype=torch.float).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'],dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],dtype=torch.float).view(-1, 1).to(self.device)

        next_q_values = self.target_critic(
            torch.cat(
                [next_states, self.target_actor(next_states)], dim=1))
        q_targets = rewards + self.gamma * next_q_values * (1 - dones)
        critic_loss = torch.mean(
            F.mse_loss(
                # MSE损失函数
                self.critic(torch.cat([states, actions], dim=1)),
                q_targets))
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        actor_loss = -torch.mean(
            self.critic(
                # 策略网络就是为了使得Q值最大化
                torch.cat([states, self.actor(states)], dim=1)))
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        self.soft_update(self.actor, self.target_actor)  # 软更新策略网络
        self.soft_update(self.critic, self.target_critic)  # 软更新价值网络

actor_lr = 5e-4
critic_lr = 5e-3
num_episodes = 200
hidden_dim = 64
gamma = 0.98
tau = 0.005  # 软更新参数
buffer_size = 10000
minimal_size = 1000
batch_size = 64
sigma = 0.01  # 高斯噪声标准差
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
    "cpu")

env_name = 'Pendulum-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0]  # 动作最大值
agent = DDPG(state_dim, action_dim, state_dim + action_dim, hidden_dim, False,
             action_bound, sigma, actor_lr, critic_lr, tau, gamma, device)

return_list = train_off_policy_agent(env, agent, num_episodes,replay_buffer, minimal_size,batch_size)

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()

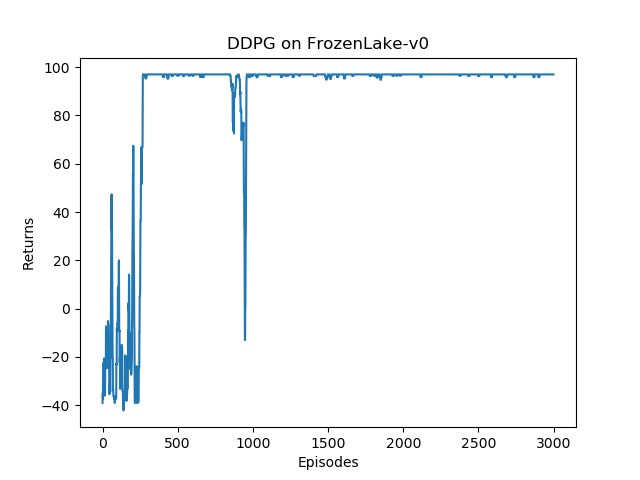
可以发现DDPG在倒立摆环境中表现出很不错的效果，其学习速度非常快，并且不需要太多样本。

3.4，算法实现（离散动作空间） 

强化学习（实践）：多智能体强化学习_燕双嘤的博客-CSDN博客_多智能体强化1，基本概念1.1，环境设置Fully cooperative（完全合作关系）：Agent利益一致，获得的奖励相同，有共同的目标。Fully comperative（完全竞争关系）：一方获得的奖励是另一方的损失。比如比赛场上的两个机器人。Mixed Cooperative & competitive（混合关系）：既有竞争，也有合作。例如：足球机器人，两支球队是竞争关系，每个队伍内部是合作关系。Self-interested （利己主义）：一个Agent的动作会改变环境的状态，此https://blog.csdn.net/qq_42192693/article/details/124164161?spm=1001.2014.3001.5501原理：MADDPG小节Gumbel-Softmax

import random
import gym
import numpy as np
import torch
from torch import nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
from tqdm import tqdm
import rl_utils
from env import  CliffWalkingEnv

class TwoLayerFC(torch.nn.Module):
    def __init__(self, num_in, num_out, hidden_dim):
        super().__init__()
        self.fc1 = torch.nn.Linear(num_in, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = torch.nn.Linear(hidden_dim, num_out)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        return self.fc3(x)
def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state,True)
                    next_state, reward, done = env.step(action)
                    #print(next_state, reward, done)
                    replay_buffer.add(state, list(action.detach().numpy()[0]), reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

class DDPG:
    ''' DDPG算法 '''
    def __init__(self, state_dim, action_dim, critic_input_dim, hidden_dim, sigma, actor_lr,critic_lr, tau, gamma):
        self.actor = TwoLayerFC(state_dim, action_dim, hidden_dim)
        self.target_actor = TwoLayerFC(state_dim, action_dim, hidden_dim)
        self.critic = TwoLayerFC(critic_input_dim, 1, hidden_dim)
        self.target_critic = TwoLayerFC(critic_input_dim, 1, hidden_dim)
        self.target_critic.load_state_dict(self.critic.state_dict())
        self.target_actor.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
        self.critic_criterion = torch.nn.MSELoss()
        self.gamma = gamma
        self.sigma = sigma  # 高斯噪声的标准差,均值直接设为0
        self.tau = tau  # 目标网络软更新参数
        self.action_dim = action_dim

    def take_action(self, state, explore):
        state=torch.tensor([state], dtype=torch.float)
        action = self.actor(state)
        if explore:
            action = rl_utils.gumbel_softmax(action)
        else:
            action = rl_utils.onehot_from_logits(action)
        return action

    def soft_update(self, net, target_net):
        for param_target, param in zip(target_net.parameters(), net.parameters()):
            param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float)
        actions = torch.tensor(transition_dict['actions'], dtype=torch.float)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float)
        self.critic_optimizer.zero_grad()
        # next_q_values = self.target_critic(torch.cat([next_states, self.target_actor(next_states)], dim=1))
        # q_targets = rewards.reshape(64,1) + self.gamma * (next_q_values) * (1 - dones.reshape(64,1))
        # critic_loss = torch.mean(F.mse_loss(self.critic(torch.cat([states, actions], dim=1)),q_targets))
        # critic_loss.backward()
        all_target_act = rl_utils.onehot_from_logits(self.target_actor(next_states))
        target_critic_input = torch.cat((next_states, all_target_act), dim=1)
        target_critic_value = rewards.view(-1, 1) + self.gamma * self.target_critic(target_critic_input) * (1 - dones.view(-1, 1))
        critic_input = torch.cat((states, actions), dim=1)
        critic_value = self.critic(critic_input)
        critic_loss = self.critic_criterion(critic_value, target_critic_value.detach())
        critic_loss.backward()
        self.critic_optimizer.step()

        self.actor_optimizer.zero_grad()
        cur_actor_out = self.actor(states)
        cur_act_vf_in = rl_utils.gumbel_softmax(cur_actor_out)
        #actor_loss = -torch.mean(self.critic(torch.cat([states, self.actor(states)], dim=1)))
        vf_in = torch.cat([states, cur_act_vf_in], dim=1)
        actor_loss = -self.critic(vf_in).mean()
        actor_loss += (cur_actor_out ** 2).mean() * 1e-3

        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        self.soft_update(self.actor, self.target_actor)  # 软更新策略网络
        self.soft_update(self.critic, self.target_critic)  # 软更新价值网络

actor_lr = 5e-4
critic_lr = 5e-3
num_episodes = 3000
hidden_dim = 64
gamma = 0.98
tau = 0.005  # 软更新参数
buffer_size = 10000
minimal_size = 2000
batch_size = 64
sigma = 0.01  # 高斯噪声标准差

env_name = 'FrozenLake-v0'
ncol = 5
nrow = 5
end = (3,1)
env = CliffWalkingEnv(ncol, nrow,end)
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = 25
action_dim = 4
agent = DDPG(state_dim, action_dim, state_dim + action_dim, hidden_dim, sigma, actor_lr, critic_lr, tau, gamma)

return_list = train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size)
print(max(return_list))
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()

rl_untils

from tqdm import tqdm
import numpy as np
import torch
import collections
import random
import torch.nn.functional as F

class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)

    def add(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):
        return len(self.buffer)

def onehot_from_logits(logits, eps=0.01):
    ''' 生成最优动作的独热（one-hot）形式 '''
    argmax_acs = (logits == logits.max(1, keepdim=True)[0]).float()
    # 生成随机动作,转换成独热形式
    rand_acs = torch.autograd.Variable(
        torch.eye(logits.shape[1])[[np.random.choice(range(logits.shape[1]), size=logits.shape[0])]],
        requires_grad=False).to(logits.device)
    # 通过epsilon-贪婪算法来选择用哪个动作
    return torch.stack([argmax_acs[i] if r > eps else rand_acs[i] for i, r in enumerate(torch.rand(logits.shape[0]))])

def sample_gumbel(shape, eps=1e-20, tens_type=torch.FloatTensor):
    """从Gumbel(0,1)分布中采样"""
    U = torch.autograd.Variable(tens_type(*shape).uniform_(), requires_grad=False)
    return -torch.log(-torch.log(U + eps) + eps)

def gumbel_softmax_sample(logits, temperature):
    """ 从Gumbel-Softmax分布中采样"""
    y = logits + sample_gumbel(logits.shape, tens_type=type(logits.data)).to(logits.device)
    return F.softmax(y / temperature, dim=1)


def gumbel_softmax(logits, temperature=1.0):
    """从Gumbel-Softmax分布中采样,并进行离散化"""
    y = gumbel_softmax_sample(logits, temperature)
    y_hard = onehot_from_logits(y)
    y = (y_hard.to(logits.device) - y).detach() + y
    # 返回一个y_hard的独热量,但是它的梯度是y,我们既能够得到一个与环境交互的离散动作,又可以
    # 正确地反传梯度
    return y
def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0))
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size - 1, 2)
    begin = np.cumsum(a[:window_size - 1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

env

import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm  # tqdm是显示循环进度条的库
import torch

class CliffWalkingEnv:
    def __init__(self, ncol, nrow, end):
        self.nrow = nrow
        self.index = 0
        self.ncol = ncol
        self.x = 0  # 记录当前智能体位置的横坐标
        self.y = 0  # 记录当前智能体位置的纵坐标
        self.end = end
        self.visited= [(0,0)]

    def step(self, action):  # 外部调用这个函数来让当前位置改变
        action = torch.argmax(action[0]).item()
        if action == 0:
            self.x -= 1  # left
        elif action == 1:
            self.x += 1  # right
        elif action == 2:
            self.y += 1  # down
        elif action == 3:
            self.y -= 1  # up
        if self.x < 0:
            self.x = 0
        # reward = -2
        if self.x >= self.nrow:
            self.x = self.nrow - 1
            # reward = -2
        if self.y < 0:
            self.y = 0
            # reward = -2
        if self.y >= self.ncol:
            self.y = self.ncol - 1
            # reward = -2
        next_state = [0] * 25
        next_state[self.y * self.ncol + self.x] = 1
        done = False
        if (self.x,self.y) in self.visited:
            reward = -5
        else:
            reward = -1
        if self.index>=10:
            done = True
        self.index += 1
        self.visited.append((self.x, self.y))
        if self.end == (self.x, self.y) :  # End
            reward = 100
            done = True
        return next_state, reward, done

    def reset(self):  # 回归初始状态，坐标轴原点在左上角
        self.index = 0
        self.x = 0
        self.y = 0
        self.visited = [(0, 0)]
        next_state = [0] * 25
        next_state[0] = 1
        return next_state

Iteration 0: 100%|██████████| 300/300 [00:08<00:00, 35.10it/s, episode=300, return=96.500]
Iteration 1: 100%|██████████| 300/300 [00:09<00:00, 30.35it/s, episode=600, return=97.000]
Iteration 2: 100%|██████████| 300/300 [00:12<00:00, 24.88it/s, episode=900, return=96.000]
Iteration 3: 100%|██████████| 300/300 [00:10<00:00, 27.47it/s, episode=1200, return=96.000]
Iteration 4: 100%|██████████| 300/300 [00:10<00:00, 28.82it/s, episode=1500, return=96.000]
Iteration 5: 100%|██████████| 300/300 [00:10<00:00, 29.16it/s, episode=1800, return=97.000]
Iteration 6: 100%|██████████| 300/300 [00:10<00:00, 28.16it/s, episode=2100, return=97.000]
Iteration 7: 100%|██████████| 300/300 [00:18<00:00, 16.40it/s, episode=2400, return=97.000]
Iteration 8: 100%|██████████| 300/300 [00:15<00:00, 19.88it/s, episode=2700, return=97.000]
Iteration 9: 100%|██████████| 300/300 [00:13<00:00, 22.37it/s, episode=3000, return=97.000]