Scikit-learn

Scikit-learn

Scikit-learn简介

​ 第三方模块，对机器学习的算法进行了封装，包括回归、降维、分类和聚类四大机器学习方法。是Scipy模块的扩展，建立在Numpy和Matplotlib基础上，是简单高效的数据挖掘和数据分析工具。

Scikit-learn安装

pip install -U scikit-learn

要求python版本高于2.7版本，Numpy版本高于1.8.2。

线性模型

Scikit-learn对于繁琐的线性回归求解数学过程设计好了线性模型，通过直接调用其linear_model模块就可以实现线性回归分析。linear-model模块中提供了包括最小二乘法回归、岭回归、Lasso、贝叶斯回归等等。

线性回归：线性回归是利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析与预测的方法，应用十分广泛。在线性回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果线性回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。（百度百科）

最小二乘法回归

参考链接

• https://www.zhihu.com/question/37031188
• https://blog.csdn.net/MarsJohn/article/details/54911788
• https://blog.csdn.net/u010687164/article/details/86160221

二乘即是平方，最小二乘法也称为最小平方法，通过最小化误差的平方和使得预测值与真实值无限接近。

在研究两个变量(x,y)之间的相互关系时，将一系列的数据(x1,y1)(x2,y2)…(xn,yn)描绘到x-y坐标系中，寻找一条直线，使得数据的这些点都在这条直线附近。直线方程的表达式为
$$Y_i=a_0+a_1{x}_i$$
通过算术平均数可以使误差最小，确定a0，a1的计算公式如下：
$$a_1=\frac{n{\sum }_{i=1}^n{x}_i{y}_i-{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{y}_i}{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}$$

$$a_0=\frac{{\sum }_{i=1}^n{y}_i}{n}-a_1\frac{{\sum }_{i=1}^n{x}_i}{n}$$

公式推导过程参考https://blog.csdn.net/MarsJohn/article/details/54911788

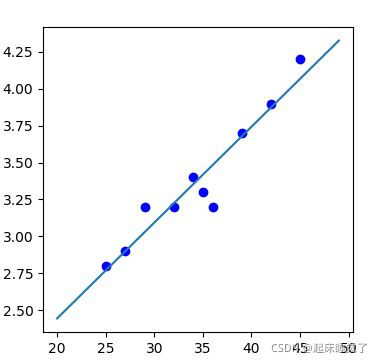
示例

import matplotlib.pyplot as plt
import numpy as np

x1=[25,27,29,32,34,36,35,39,42,45]
y1=[2.8,2.9,3.2,3.2,3.4,3.2,3.3,3.7,3.9,4.2]

fig=plt.figure(figsize=(4,4))
ax=fig.add_subplot(1,1,1)
ax.scatter(x1,y1,c='b')

x=np.arange(20,50)
y=0.0649 * x + 1.1464   #它通过公式计算的a1=0.06493 a0=1.1464
plt.plot(x,y)

plt.show()

在linear_model模块中实现最小二乘法回归的函数为LinearRegression：

linear_model.LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=None)

fit_intercept	是否需要计算截距
normalize	是否需要标准化
copy_X	是否复制X数据
n_jobs	CPU工作效率的核数(-1时所有核都工作)

LinearRegression函数的主要方法：

fit（X,y,sample_weight=None）	拟合线性模型
predict(X)	使用线性模型返回预测数据
score(X,y,sample_weight=None)	返回预测的确定系数R^2

示例

from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

data=[[56,7800],[104,9000],[156,9200],[200,10000],[250,11000],[300,12000]]
columns=['面积','价格']
df=pd.DataFrame(data=data,columns=columns)
x=pd.DataFrame(df['面积'])
y=pd.DataFrame(df['价格'])
print(df)
clf = linear_model.LinearRegression()
clf.fit (x,y)    #拟合线性模型
k=clf.coef_      #回归系数
b=clf.intercept_ #截距
x0=np.array([[170]])
#通过给定的x0预测y0，y0=截距+X值*回归系数
y0=clf.predict(x0) #预测值
print('回归系数：',k)
print('截距：',b)
print('预测值：',y0)

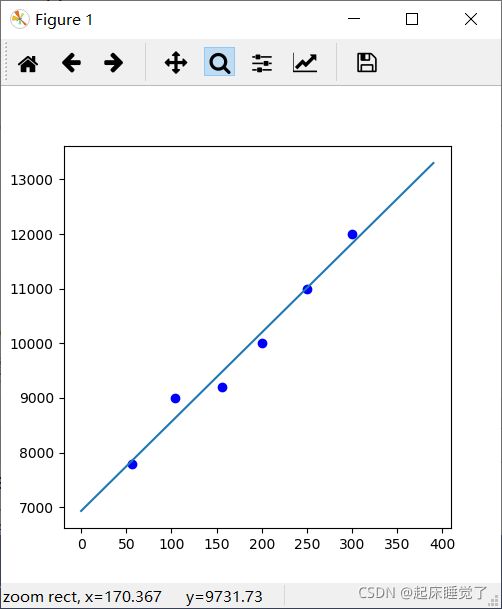
fig=plt.figure(figsize=(5,5))
ax=fig.add_subplot(1,1,1)
ax.scatter(x,y,c='b')

x=np.arange(0,400,10)
y=16.32229076* x + 6933.4063421
plt.plot(x,y)
plt.show()

输出结果

    面积     价格
0   56   7800
1  104   9000
2  156   9200
3  200  10000
4  250  11000
5  300  12000
回归系数： [[16.32229076]]
截距： [6933.4063421]
预测值： [[9708.19577086]]

岭回归

​ 岭回归是一种改进的最小二乘估计法，通过放弃最小二乘法的无偏性、以损失信息来达到使回归系数更加可靠的回归方法。对于某些数据来说，其中的某个数据的变动较大，对最后的回归系数产生较大影响，即最小二乘法回归的不足之处，岭回归便是在该方面进行了改进。在原先的线性回归残差平方和中加入了惩罚函数，保证了回归系数的稳定。

​ 岭回归模型通过在相关矩阵中引入一个很小的岭参数K（1>K>0），并将它加到主对角线元素上，从而降低参数的最小二乘估计中复共线特征向量的影响，减小复共线变量系数最小二乘估计的方法，以保证参数估计更接近真实情况。岭回归分析将所有的变量引入模型中，比逐步回归分析提供更多的信息。

岭回归https://zhuanlan.zhihu.com/p/25013568

岭回归主要使用linear_model模块的Ridge函数：

linear_model.Ridge(alpha=1.0,fit_intercept=True,normalize=False,copy_X=True,max_iter=None,tol=0.001,solver='auto',random_state=None)

alpha	权重
fit_intercept	是否需要计算截距
normalize	输入样本特征的归一化
copy_X	复制
max_iter	最大迭代次数
tol	控制求解的精度
solver	求解器(auto、svd、cholesky、sparse_cg、lsqr)

主要方法

fit(X,y)	拟合线性模型
predict(X)	使用线性模型返回预测数据

from sklearn.linear_model import Ridge
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

data=[[56,7800],[104,9000],[156,9200],[200,10000],[250,11000],[300,12000]]
columns=['面积','价格']
df=pd.DataFrame(data=data,columns=columns)
x=pd.DataFrame(df['面积'])
y=pd.DataFrame(df['价格'])
print(df)
clf = Ridge(alpha=1.0)
clf.fit (x,y)    #拟合线性模型
k=clf.coef_      #回归系数
b=clf.intercept_ #截距
x0=np.array([[170]])
#通过给定的x0预测y0，y0=截距+X值*回归系数
y0=clf.predict(x0) #预测值
print('回归系数：',k)
print('截距：',b)
print('预测值：',y0)

fig=plt.figure(figsize=(5,5))
ax=fig.add_subplot(1,1,1)
ax.scatter(x,y,c='b')

x=np.arange(0,400,10)
y=16.32229076* x + 6933.4063421
plt.plot(x,y)
plt.show()

    面积     价格
0   56   7800
1  104   9000
2  156   9200
3  200  10000
4  250  11000
5  300  12000
回归系数： [[16.32189646]]
截距： [6933.47639485]
预测值： [[9708.19879377]]

Lasso回归

Lasso回归于岭回归非常相似，它们的差别在于使用了不同的正则化项。最终都实现了约束参数从而防止过拟合的效果。除此之外岭回归无法剔除变量，而Lasso回归模型可以将一些不重要的回归系数缩减为0，达到剔除变量的目的。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SlqWVYuI-1635244857705)(C:\Users\小傻子\AppData\Roaming\Typora\typora-user-images\image-20211025182315456.png)]

其中ESS(β)= 表示误差平方和，λl1(β)表示惩罚项。

函数信息官方：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html

岭回归主要使用linear_model模块的Lasso函数：

linear_model.Lasso(alpha=1.0,fit_intercept=True, normalize=False，copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='random')

alpha	权重
fit_intercept	是否计算此模型的截距
normalize	是否进行归一化标准化
copy_X	X 被复制或是覆盖
max_iter	最大迭代次数
tol	浮动精度
positive	强制系数为正
selection	如果设置为 ‘random’，则每次迭代都会更新一个随机系数，而不是默认按顺序循环遍历特征。这（设置为“随机”）通常会显着加快收敛速度，尤其是当 tol 高于 1e-4 时。

主要方法：

fit(X,y)	拟合线性模型
score(X,y)	返回预测的确定系数
predict（X)	使用线性模型返回预测数据

from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

data=[[56,7800],[104,9000],[156,9200],[200,10000],[250,11000],[300,12000]]
columns=['面积','价格']
df=pd.DataFrame(data=data,columns=columns)
x=pd.DataFrame(df['面积'])
y=pd.DataFrame(df['价格'])
print(df)
clf = linear_model.Lasso()
clf.fit (x,y)    #拟合线性模型
k=clf.coef_      #回归系数
b=clf.intercept_ #截距
x0=np.array([[170]])
#通过给定的x0预测y0，y0=截距+X值*回归系数
y0=clf.predict(x0) #预测值
print('回归系数：',k)
print('截距：',b)
print('预测值：',y0)

fig=plt.figure(figsize=(5,5))
ax=fig.add_subplot(1,1,1)
ax.scatter(x,y,c='b')

x=np.arange(0,400,10)
y=16.32229076* x + 6933.4063421
plt.plot(x,y)
plt.show()

    面积     价格
0   56   7800
1  104   9000
2  156   9200
3  200  10000
4  250  11000
5  300  12000
回归系数： [16.32214581]
截距： [6933.43209379]
预测值： [9708.1968821]

支持向量机

支持向量

感知机的模型就是尝试找到一条直线，能够把二元数据隔离开。放到三维空间或者更高维的空间，感知机的模型就是尝试找到一个超平面，能够把所有的二元类别隔离开。对于这个分离的超平面，我们定义为wTx+b=0wTx+b=0。在优化时我们希望所有的点都被准确分类。但是实际上离超平面很远的点已经被正确分类，它对超平面的位置没有影响。我们最关心是那些离超平面很近的点，这些点很容易被误分类。如果所有的样本不光可以被超平面分开，还和超平面保持一定的函数距离（下图函数距离为1），那么这样的分类超平面是比感知机的分类超平面优的。可以证明，这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量，我们定义为支持向量。

待续。。。