python使用蒙特卡洛树(MCTS)算法实现黑白棋miniAlphaGo for Reversi
黑白棋(reversi),也叫苹果棋,翻转棋,是一个经典的策略性游戏。一般棋子双面为黑白两色,故称“黑白棋”。因为行棋之时将对方棋子翻转,变为己方棋子,故又称“翻转棋”。棋子双面为红、绿色的成为“苹果棋”。它使用8*8的棋盘,由两人执黑子和白子轮流下棋,最后子多方为胜。
规则:
(1) 黑方先行,双方交替下棋。
(2) 一步合法的棋步包含:在一个空格新落下一个棋子,并且反转对手一个或多个棋子。
(3) 新落下的棋子与棋盘上已有的同色棋子间,对方被夹住的所有棋子都要反转过来。可以横着夹,竖着夹,斜着夹。夹住的位置上必须全部都是对手的棋子,不能有空格。
(4) 一步棋可以在数个(横向、纵向、对角线)方向上翻棋,任何被夹住的棋子都必须被翻转过来,棋手无权选择不去翻某个棋子。
(5) 除非至少翻转了对手的一个棋子,否则就不能落子。如果一方没有合法棋步,也就是说不管他下到哪里,都不能至少翻转对手的一个棋子,那他这一轮 只能弃权,而由他的对手继续落子直到他有合法棋步可下。
(6) 如果一方至少有一步合法棋步可下,他就必须落子,不得弃权。
(7) 棋局持续下去,直到棋盘填满或者双方都无合法棋步可下。
(8) 如果某一方落子时间超过1分钟,则判该方失败。
蒙特卡洛搜索树的主要核心思想
蒙特卡罗树搜索大概可以被分成四步。选择,拓展,模拟,反向传播。在开始阶段,搜索树只有一个节点,也就是我们需要决策的局面。搜索树中的每一个节点包含了三个基本信息:代表的局面,被访问的次数,累计评分。
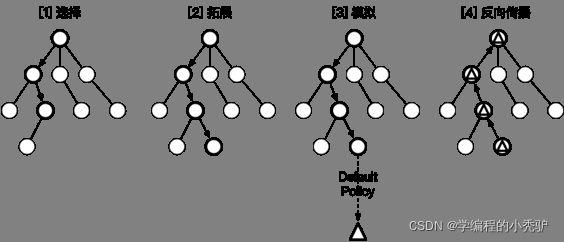
(1)选择
在选择阶段,需要从根节点,也就是要做决策的局面R出发向下选择出一个最急迫需要被拓展的节点N,局面R是是每一次迭代中第一个被检查的节点;对于被检查的局面而言,可能有三种可能:
1.该节点所有可行动作都已经被拓展过
2.该节点有可行动作还未被拓展过
3.这个节点游戏已经结束了(例如已经连成五子的五子棋局面)
对于这三种可能:
1.如果所有可行动作都已经被拓展过了,那么将使用UCB公式计算该节点所有子节点的UCB值,并找到值最大的一个子节点继续检查。反复向下迭代。
2.如果被检查的局面依然存在没有被拓展的子节点,那么认为这个节点就是本次迭代的的目标节点N,并找出N还未被拓展的动作A。执行步骤[2]
3.如果被检查到的节点是一个游戏已经结束的节点。那么从该节点直接执行步骤{4]。
每一个被检查的节点的被访问次数在这个阶段都会自增。在反复的迭代之后,我们将在搜索树的底端找到一个节点,来继续后面的步骤。
(2)扩展
在选择阶段结束时候,查找到了一个最迫切被拓展的节点N,以及他一个尚未拓展的动作A。在搜索树中创建一个新的节点Nn作为N的一个新子节点。Nn的局面就是节点N在执行了动作A之后的局面。
(3)模拟
为了让Nn得到一个初始的评分。从Nn开始,让游戏随机进行,直到得到一个游戏结局,这个结局将作为Nn的初始评分。一般使用胜利/失败来作为评分,只有1或者0。
(4)反向传播
在Nn的模拟结束之后,它的父节点N以及从根节点到N的路径上的所有节点都会根据本次模拟的结果来添加自己的累计评分。如果在[1]的选择中直接发现了一个游戏结局的话,根据该结局来更新评分。每一次迭代都会拓展搜索树,随着迭代次数的增加,搜索树的规模也不断增加。当到了一定的迭代次数或者时间之后结束,选择根节点下最好的子节点作为本次决策的结果。
实现
MCTS.py
import random
import math
import time
BOARD_SIZE = 8
PLAYER_NUM = 2
COMPUTER_NUM = 1
MAX_THINK_TIME = 60
direction = [[0, 1], [1, 1], [1, 0], [1, -1], [0, -1], [-1, -1], [-1, 0], [-1, 1]]
# 初始化棋盘数组
def getInitialBoard():
board = {}
for i in range(0, BOARD_SIZE):
board[i] = {}
for j in range(0, BOARD_SIZE):
board[i][j] = 0
board[BOARD_SIZE / 2 - 1][BOARD_SIZE / 2 - 1] = COMPUTER_NUM
board[BOARD_SIZE / 2][BOARD_SIZE / 2] = COMPUTER_NUM
board[BOARD_SIZE / 2 - 1][BOARD_SIZE / 2] = PLAYER_NUM
board[BOARD_SIZE / 2][BOARD_SIZE / 2 - 1] = PLAYER_NUM
return board
# 返回棋子数
def countTile(board, tile):
stones = 0
for i in range(0, BOARD_SIZE):
for j in range(0, BOARD_SIZE):
if board[i][j] == tile:
stones += 1
return stones
# 返回一个颜色棋子可能的下棋位置
def possible_positions(board, tile):
positions = []
for i in range(0, BOARD_SIZE):
for j in range(0, BOARD_SIZE):
if board[i][j] != 0:
continue
if updateBoard(board, tile, i, j, checkonly=True) > 0:
positions.append((i, j))
return positions
def isOnBoard(x, y):
return x >= 0 and x <= 7 and y >= 0 and y <= 7
# 是否是合法走法,如果合法返回需要翻转的棋子列表
def updateBoard(board, tile, i, j, checkonly=False):
# 该位置已经有棋子或者出界了,返回False
reversed_stone = 0
# 临时将tile 放到指定的位置
board[i][j] = tile
if tile == 2:
change = 1
else:
change = 2
# 要被翻转的棋子
need_turn = []
for xdirection, ydirection in direction:
x, y = i, j
x += xdirection
y += ydirection
if isOnBoard(x, y) and board[x][y] == change:
x += xdirection
y += ydirection
if not isOnBoard(x, y):
continue
# 一直走到出界或不是对方棋子的位置
while board[x][y] == change:
x += xdirection
y += ydirection
if not isOnBoard(x, y):
break
# 出界了,则没有棋子要翻转
if not isOnBoard(x, y):
continue
# 是自己的棋子,中间的所有棋子都要翻转
if board[x][y] == tile:
while True:
x -= xdirection
y -= ydirection
# 回到了起点则结束
if x == i and y == j:
break
# 需要翻转的棋子
need_turn.append([x, y])
# 将前面临时放上的棋子去掉,即还原棋盘
board[i][j] = 0 # restore the empty space
# 没有要被翻转的棋子,则走法非法。翻转棋的规则。
for x, y in need_turn:
if not (checkonly):
board[i][j] = tile
board[x][y] = tile # 翻转棋子
reversed_stone += 1
return reversed_stone
# 蒙特卡洛树搜索
def mctsNextPosition(board):
def ucb1(node_tuple, t, cval):
name, nplayout, reward, childrens = node_tuple
if nplayout == 0:
nplayout = 0.00000000001
if t == 0:
t = 1
#reward 是赢的次数 nplayout是模拟对局次数,cval是常数
return (reward / nplayout) + cval * math.sqrt(2 * math.log(t) / nplayout)
def find_playout(tep_board, tile, depth=0):
def eval_board(tep_board):
player_tile = countTile(tep_board, PLAYER_NUM)
computer_tile = countTile(tep_board, COMPUTER_NUM)
if computer_tile > player_tile:
return True
return False
if depth > 32:
return eval_board(tep_board)
turn_positions = possible_positions(tep_board, tile)
# 查看是否可以在这个位置下棋
if len(turn_positions) == 0:
if tile == COMPUTER_NUM:
neg_turn = PLAYER_NUM
else:
neg_turn = COMPUTER_NUM
neg_turn_positions = possible_positions(tep_board, neg_turn)
if len(neg_turn_positions) == 0:
return eval_board(tep_board)
else:
tile = neg_turn
turn_positions = neg_turn_positions
# 随机放置一个棋子
temp = turn_positions[random.randrange(0, len(turn_positions))]
updateBoard(tep_board, tile, temp[0], temp[1])
# 转换轮次
if tile == COMPUTER_NUM:
tile = PLAYER_NUM
else:
tile = COMPUTER_NUM
return find_playout(tep_board, tile, depth=depth + 1)
def expand(tep_board, tile):
positions = possible_positions(tep_board, tile)
result = []
for temp in positions:
result.append((temp, 0, 0, []))
return result
def find_path(root, total_playout):
current_path = []
child = root
parent_playout = total_playout
isMCTSTurn = True
while True:
if len(child) == 0:
break
maxidxlist = [0]
cidx = 0
if isMCTSTurn:
maxval = -1
else:
maxval = 2
for n_tuple in child:
parent, t_playout, reward, t_childrens = n_tuple
#实现最大最小搜索,电脑选择最大值,玩家选择最小值
if isMCTSTurn:
cval = ucb1(n_tuple, parent_playout, 0.1)
if cval >= maxval:
if cval == maxval:
maxidxlist.append(cidx)
else:
maxidxlist = [cidx]
maxval = cval
else:
cval = ucb1(n_tuple, parent_playout, -0.1)
if cval <= maxval:
if cval == maxval:
maxidxlist.append(cidx)
else:
maxidxlist = [cidx]
maxval = cval
cidx += 1
# 随机进行下棋,扩展
maxidx = maxidxlist[random.randrange(0, len(maxidxlist))]
parent, t_playout, reward, t_childrens = child[maxidx]
current_path.append(parent)
parent_playout = t_playout
child = t_childrens
isMCTSTurn = not (isMCTSTurn)
return current_path
root = expand(board, COMPUTER_NUM)
current_board = getInitialBoard()
current_board2 = getInitialBoard()
start_time = time.time()
for loop in range(0, 5000):
# 思考最大时间限制
if (time.time() - start_time) >= MAX_THINK_TIME:
break
# current_path是一个放置棋子的位置列表,根据此列表进行后续操作
current_path = find_path(root, loop)
tile = COMPUTER_NUM
for temp in current_path:
updateBoard(current_board, tile, temp[0], temp[1])
if tile == COMPUTER_NUM:
tile = PLAYER_NUM
else:
tile = COMPUTER_NUM
#复制棋盘,因为会在find_playout函数修改了棋盘
isWon = find_playout(current_board2, tile)
#自顶向下传递参数
child = root
for temp in current_path:
idx = 0
for n_tuple in child:
parent, t_playout, reward, t_childrens = n_tuple
if temp[0] == parent[0] and temp[1] == parent[1]:
break
idx += 1
if temp[0] == parent[0] and temp[1] == parent[1]:
t_playout += 1
if isWon:
reward += 1
if t_playout >= 5 and len(t_childrens) == 0:
t_childrens = expand(current_board, tile)
child[idx] = (parent, t_playout, reward, t_childrens)
child = t_childrens
print("loop count: ", loop)
max_avg_reward = -1
mt_result = (0, 0)
for n_tuple in root:
parent, t_playout, reward, t_childrens = n_tuple
if (t_playout > 0) and (reward / t_playout > max_avg_reward):
mt_result = parent
max_avg_reward = reward / t_playout
return mt_result
Game.py
import MCTS as rvs
import tkinter as Tk
import time
import tkinter.messagebox
total=[]
class ReversiBoard(Tk.Canvas):
cell_size = 46
margin = 5
board = rvs.getInitialBoard()
validBoard = True
isPayerTurn = True
step = []
def __init__(self, master):
cwidth = rvs.BOARD_SIZE * self.cell_size
Tk.Canvas.__init__(self, master, relief=Tk.RAISED, bd=4, bg='white', width=cwidth, height=cwidth,cursor="cross")
self.bind("<1>", self.put_stones)
for i in range(rvs.BOARD_SIZE):
for j in range(rvs.BOARD_SIZE):
bcolor = "#F5F5DC"
x0 = i * self.cell_size + self.margin
y0 = j * self.cell_size + self.margin
self.create_rectangle(x0, y0, x0 + self.cell_size, y0 + self.cell_size, fill=bcolor, width=1)
self.refresh()
def put_stones(self, event): # 放置棋子
# 是否游戏结束
if self.validBoard == False:
self.validBoard = True
self.board = rvs.getInitialBoard()
self.isPayerTurn = True
for numid in self.step:
self.delete(numid)
self.step = []
self.refresh()
return
# 电脑轮次
if not (self.isPayerTurn):
return
# 玩家轮次
x = self.canvasx(event.x)
y = self.canvasy(event.y)
# 获得坐标
i = int(x / self.cell_size)
j = int(y / self.cell_size)
if self.board[i][j] != 0 or rvs.updateBoard(self.board, rvs.PLAYER_NUM, i, j, checkonly=True) == 0:
return
rvs.updateBoard(self.board, rvs.PLAYER_NUM, i, j)
self.refresh()
isPayerTurn = False
self.after(100, self.AI_move)
def AI_move(self):
while True:
player_possibility = len(rvs.possible_positions(self.board, rvs.PLAYER_NUM))
mcts_possibility = len(rvs.possible_positions(self.board, rvs.COMPUTER_NUM))
if mcts_possibility == 0:
break
start= time.time()
stone_pos = rvs.mctsNextPosition(self.board)
end =time.time()
one_time=end-start
print("Computer position:", stone_pos)
print("Step time:",format(one_time, '.4f'),"s")
total.append(one_time)
rvs.updateBoard(self.board, rvs.COMPUTER_NUM, stone_pos[0], stone_pos[1])
self.refresh()
player_possibility = len(rvs.possible_positions(self.board, rvs.PLAYER_NUM))
mcts_possibility = len(rvs.possible_positions(self.board, rvs.COMPUTER_NUM))
if mcts_possibility == 0 or player_possibility > 0:
break
if player_possibility == 0 and mcts_possibility == 0:
self.showResult()
self.validBoard = False
self.isPayerTurn = True
def showResult(self):
player_stone = rvs.countTile(self.board, rvs.PLAYER_NUM)
mcts_stone = rvs.countTile(self.board, rvs.COMPUTER_NUM)
if player_stone > mcts_stone:
tkinter.messagebox.showinfo('游戏结束', "你获胜了")
elif player_stone == mcts_stone:
tkinter.messagebox.showinfo('游戏结束', "平局")
else:
tkinter.messagebox.showinfo('游戏结束', "你失败了")
print(sum(total))
def refresh(self):
for i in range(rvs.BOARD_SIZE):
for j in range(rvs.BOARD_SIZE):
x0 = i * self.cell_size + self.margin
y0 = j * self.cell_size + self.margin
if self.board[i][j] == 0:
continue
if self.board[i][j] == rvs.PLAYER_NUM:
bcolor = "#000000"
if self.board[i][j] == rvs.COMPUTER_NUM:
bcolor = "#ffffff"
self.create_oval(x0 + 2, y0 + 2, x0 + self.cell_size - 2, y0 + self.cell_size - 2, fill=bcolor,
width=0)
class Reversi(Tk.Frame):
def __init__(self, master=None):
Tk.Frame.__init__(self, master)
self.master.title("黑白棋")
l_title = Tk.Label(self, text='Reversi_AI', font=('Times', '24', ('italic', 'bold')), fg='#191970', bg='#EEE8AA',
width=12)
#l_title.pack(padx=10, pady=10)
self.f_board = ReversiBoard(self)
self.f_board.pack(padx=10, pady=10)
if __name__ == '__main__':
app = Reversi()
app.pack()
app.mainloop()