时空图学习笔记：Structural-RNN: Deep Learning on Spatio-Temporal Graphs

                                                               

论文链接：https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/Jain_Structural-RNN_Deep_Learning_CVPR_2016_paper.pdf

此为原创笔记，如需转载请注明

                     时空图和结构化RNN: st-graph and structural-RNN

目录

                     时空图和结构化RNN: st-graph and structural-RNN

 

一、时空图（Spatio-temporal graph）

1.时空图

2.时空图展开

3.因子图

3.1 因子图

3.2  因子/参数共享

二、时空图到Structural-RNN转化

1.转化过程——二分图

2.算法

三、Strctural-RNN训练过程

 

---

 

本论文讲解的的是如何通过人的特征（人体姿态特征）、物的特征（物的功能特征等）以及人和静态物体的关系（相对位置关系特征等），来判断每个时间点t=1,2,3,...人所做的动作。

一、时空图（Spatio-temporal graph）

1.概念

（以 人、碗、微波炉的例子进行讲解）

                                        

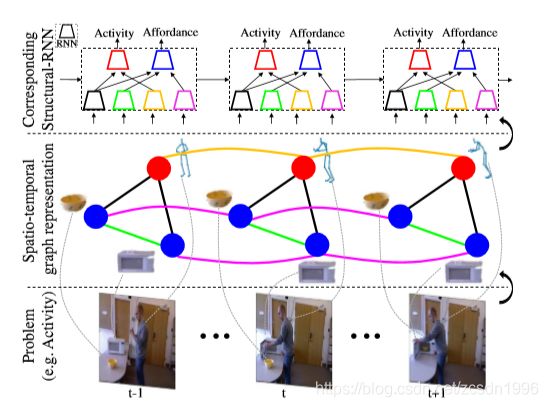
   图1：从st图到S-RNN的示例问题。（底部）显示了一个示例活动（人体微波食品）。对这些问题进行建模需要空间和时间两方面的推理。（中）捕捉人与物体之间的时空交互作用的St-graph。（顶部）我们的结构RNN体系结构的示意图，自动从st图形派生。它以一种丰富而可伸缩的方式捕捉st-graph的结构和交互作用。

    时空图（st-graph）：是一种用于刻画多个物体之间在空间与时间维度上交互的图结构。

                                          

                                                                    简化的时空图

   时空图三要素：节点，时空边（spatio-temporal edge）和时间边（temporal edge）

                                                                               其中v∈V，

      （1）节点V：人和物体                                                          例子中为人、碗、微波炉

      （2）时空边集：同一时间，人-人，人-物之间的关系       例子中为边（人，碗），边（人，微波炉），边（碗，微波炉）

      （3）时间边集：同一节点在相邻时间步上的关系             例子中为边（人，人），边（碗，碗），边（微波炉，微波炉）           

     nodes的种类：human、object

     edges的种类：human-human（self）、human-object、object-object（self）、object-object

                                  

 

2.时空图展开

按时间展开的时空图：                             

其中， 给定时间步t处的节点与无向时空边相连，相邻时间步上的节点（例如时间t处的节点u和时刻t+1处的节点v）与无向时间边相连。

        ：，，：表示节点的特征向量 ，如人/物的姿态：人的活动特征和物体的功能特征（affordance）

       ：,,,：表示边的特征向量，如节点间的相对位置

       给定一个st图和与图2b所示的节点和边相关联的特征向量、，目标是在每个时间步t预测节点标签（或实值向量，如每个时间步人的姿态/动作）。例如，在人和对象交互中，节点特征可以表示人和物体的姿势，而边特征可以表示它们的相对方向；该节点标签表示人类活动和物体 的affordance（物体的功能属性）。标签受其节点及其与其他节点（边）的交互作用的影响，导致整个复杂系统。这种交互作用通常用因子图参数化 。

3.因子图

3.1 因子图

    Factor Graph称作因子图，在维基百科定义中“将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个二分图叫做因子图。”

    具体在此参考文献中，st-graph借助各个nodes和edges的features得到nodes的labels，st-graph可被看做是从features到了labels的全局函数，但此全局函数过于复杂，因此基于图的语义：图由点和边组成，将st-graph整个全局函数拆分成点因子函数和边因子函数。

    该因子图表示st图上的（复杂）函数如何分解为更简单的函数[35]。我们从st图的因子图表示中导出了S-RNN体系结构。我们的因子图表示法对每个节点有一个因子函数，每个边有一个成对因子。图2c显示了与2a中st图相对应的因子图。

点因子函数：，

边因子函数：

用RNN实现这些因子函数，训练其权重。

     

 （a） 表示活动的时空图                  展开（unroll）         （b） 随时间展开             因子图            （c） 因子图参数化

图2：人类活动的时空图（st图）示例。（a） 捕捉人-对象交互的st图。（b） 通过边缘集展开st图形。节点和边用与其相关联的特征向量进行标记。（c） st图的因子图参数化。st图中的每个节点和边都有相应的因子。

3.2  因子/参数共享

 1.节点之间的共享因子

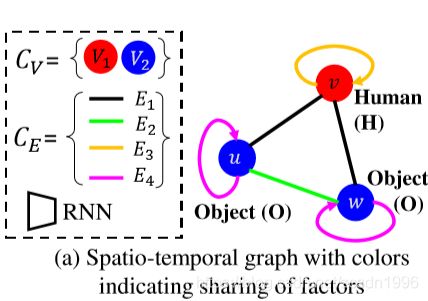
         st图中的每个因子都有需要学习的参数。语义相似的节点可以选择共享因子，而不是为每个节点学习不同的因子。例如，st图中的所有“对象节点”{u，w}可以共享相同的节点因子和参数。这种建模选择允许在相似节点之间强制参数共享。它还提供了处理具有更多节点的st图而不增加参数数量的灵活性。为此，我们将节点划分。在图3a中，我们重新绘制st图，并为共享节点因子的节点分配相同的颜色。

      节点划分：CV={V1，…，VP}，其中VP是一组语义相似的节。，它们都使用相同的节点因子。如：碗和微波炉共享因子

     共享因子：它们都使用相同的节点因子。

 

2. 边之间共享因子

    边划分   ：={E1，…，EM}，其中EM是一组边的集合，这些边的节点组成一个语义对。

    共享因子：集合中的所有边共享相同的边因子。例如，所有的“人类对象边缘”{（v，u），（v，w）}都是用相同的边缘因子建模。即用一个RNN实现。

    基于语义的共享因子使得整体参数化紧凑。事实上，共享参数对于处理节点数量取决于上下文的应用程序是必需的。例如，在人与对象交互中，对象节点的数量随环境而变化。因此，如果不在对象节点之间共享参数，模型就不能推广到具有更多对象的新环境。对于流动性建模，和中的边因子(参数）不共享。因此，在图3a中，对象-对象的时间边与对象对象的时空边的颜色不同。（即object-object表示时：时空边用绿色表示交互，时间边用紫色表示交互，但都是object-object的交互）                 （在轨迹预测中这些静态物体对人的影响一样，自然可以共享因子）

 

3.共享因子时空图

    为了预测节点v∈Vp的标签，我们考虑其节点因子，以及因子图中与v相连的边因子。如果节点因子和边因子共同影响st图中某个节点的标签，我们将它们定义为邻居。更正式地说，节点因子和边因子是相邻的，如果存在一个节点v∈Vp，使得它同时连接到因子图中的和。我们将在构建S-RNN体系结构时使用此定义，以便它捕获st图中的交互作用。

                                  

                                                    因子/参数共享后的时空图 

二、时空图到Structural-RNN转化

1.转化过程——二分图

     我们从st图的因子图表示中导出了S-RNN体系结构。st图中的因子以时间方式操作，在每个时间步中，因子观察（节点和边缘）特征并对这些特征进行一些计算。在S-RNN中，我们用RNN表示每个因子。我们把从节点因子得到的rnn称为NodeRNNs，将从边因子得到的rnn称为edgeRNNs。st图表示的交互通过nodeRNNs和edgeRNNs之间的连接来捕获。       

    在文章提出使用RNN之前，对于nodes和edges的factor function的描述是抽象的，也没有不同factors运算的层级关系，笔者没有发现如何具体地使用这些factor得出最终预测的nodes的labels。

    而在提出使用RNN充当factor function功能后，文章给出了预测labels的具体结构——二分图，左侧点是edgeRNNs，右侧点是nodeRNNs，图中所有的边均由左侧指向右侧，经右侧nodeRNNs计算后输出得到最终的labels，这样做的目的主要是使得RNNs组成的模型是一个前馈神经网络以便训练。

 图3 （a） 用颜色表示因子共享的时空图  （b） 对应S-RNN（二分图）  （c） 人节点v的前向传播 （d） 对象节点w的前向传播

 图3（b）：由st-graph转化的Strctural-RNN图形称为二分图——

                   edgeRNNs：从边因子得到的rnn称为edgeRNNs

                   nodeRNNs：从节点因子得到的rnn称为NodeRNNs

                  ：节点因子对应的RNN

                 ：边因子对应的RNN。

                 为了得到一个前馈网络，我们将边缘网络和节点网络连接起来形成一个二部图。特别地，edgeRNN 连接到节点nodeRNN   iff 因子和因子是st图中的邻居，即它们共同影响st图中某个节点的标签。综上所述，在算法1中我们给出了构造S-RNN体系结构的步骤。图3b显示了图3a所示的人类活动的S-RNN。nodeRNNs将它们连接到的edgeRNNs的输出组合起来（即因子图中它的邻居），并预测节点标签。nodeRNNs（如和）的预测通过edgeRNNs（如）相互作用。每个edgeRNN处理st-grap中连接的节点之间的特定语义交互，并对交互如何随时间演变进行建模。在下一节中，我们将解释S-RNN的输入、输出和训练过程。 

图3（c）：人-人的前向传播过程

                 人类节点v的前向传播涉及RNNs RE1、RE3和RV1。在图4中，我们展示了这个前进通道的详细布局。RE1的输 入特征是人-物体边特征的总和。

图3（d）：对象节点w的前向传播过程

                  对象节点w的前向过程涉及RNNs RE1、RE2、RE4和RV2。在该正向过程中，edgeRNN RE1仅处理边缘特征xv，w。

     

2.算法

    

 输入：st-graph:,CV={V1，…，VP}

 输出：S-RNN二分图：

步骤：

1.根据语义划分边：={E1，…，EM}

2.求st图的因子部分：{，}

3.用nodeRNN 表示每个

4.用edgeRNN 表示每个

5.连接{}和{}形成一个二分图

边（，），当存两个节点（eg:u,v）不在同一分类但是相互关联的时候

return：

 

三、Strctural-RNN训练过程

         

              图4:Human NodeV的前向传播显示了与展开的st图上的图3C相对应的体系结构布局。（彩色视图）

    为了训练S-RNN体系结构，对于st图的每个节点，与该节点相关联的特征被输入到该体系结构中。在节点v∈Vp的正向过程中， edgeRNN 的输入是边上的边特征的时间序列，其中边e与st图中的节点v相关联。每个时间步的nodeRNN 连接节点特征及其连接的edgeRNN的输出，并预测节点标签。训练时，预测误差通过前向传播过程中涉及的nodeRNN和edgeRNNs进行反向传播。这样，S-RNN非线性地结合了与节点相关的节点和边缘特征，以预测节点标签。

    图3c显示了人节点的前向传播S-RNN。图4显示了同一前向传播的详细架构布局。前向传播涉及到边（人-物边）和（人-人边）。由于人类节点v与两个对象节点{u，w}交互，我们将两个边缘特征的总和作为输入传递给。与串联相反，特征的总和对于使用固定体系结构处理可变数量的对象节点非常重要。由于对象计数随环境的变化而变化，用固定长度的特征向量来表示可变的上下文是一个挑战。根据经验，添加特性比平均池更有效。我们推测加法保留了对象计数和st图的结构，而平均池平均了边的数量。nodeRNN 将（人类）节点特征与edgeRNNs的输出连接起来，并预测每个时间步的活动。

    参数共享和结构化特征空间。S-RNN的一个重要方面是跨节点标签共享参数。当RNN在转发过程中是公共的时，节点标签之间会发生参数共享。例如，在图3c和3d中，edgeRNN 在人类节点和对象节点的正向过程中象边缘特征的线性组合。这对处理的特征施加了一个结构。更正式地说，的输入是内积，其中F是存储边缘特征很常见。此外，参数通过反向传播的梯度从对象和人类节点得到更新。这样，同时影响人和对象节点标签。

    由于人体节点连接到多个对象节点，因此输入到edgeRNN 中的始终是人体-对象边特征的线性组合。这对RE1处理的特征施加了一个结构。更正式地说，RE1的输入是内积F，其中F是存储边特征  s.t. 的特征矩阵。向量s捕捉结构化特征空间。它的条目位于{0,1}中，这取决于前向传播的节点。在上面的例子。对于人类节点，而对于对象节点。

---