HW14基于规则化的终身学习Regularization-based Lifelong Learning
文章目录
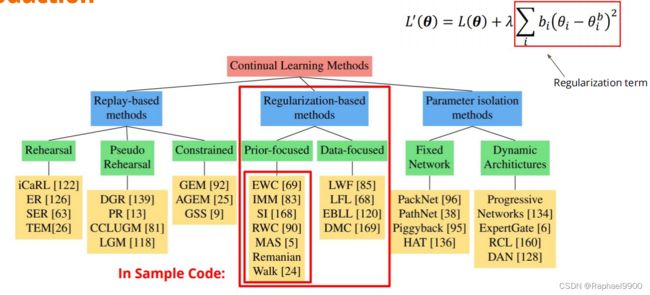
- 一、介绍-终身学习
-
-
- 目标
- 数据集
- 任务
- 示例代码-准备数据
- 模型体系结构
- 样本代码-训练和评估
- Training Pipeline:
- MAS - Memory Aware Synapse
- SI
- SCP - Sliced Cramer Preservation
-
- 二、实验
-
- 1、baseline
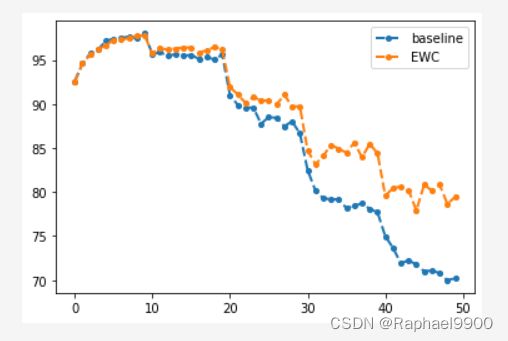
- 2、EWC
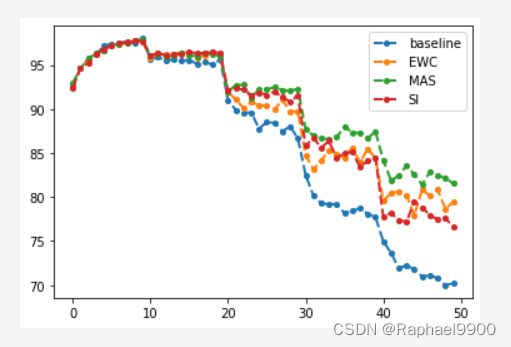
- 3、MAS
- 4、SI
- 5、RWalk
- 6、SCP
一、介绍-终身学习
目标
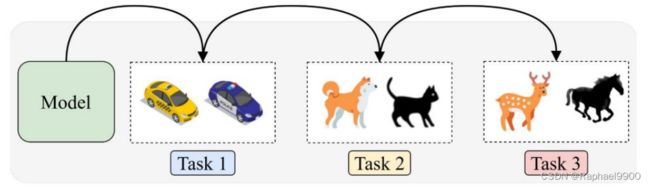
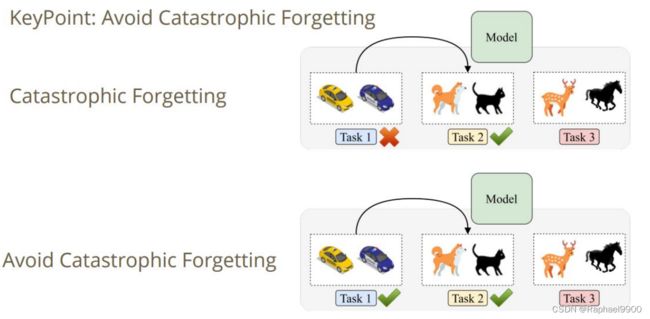
一个模型可以打败所有的任务!

条件:模型按顺序学习不同的任务!(在训练时间内)
数据集
任务
●一共五个任务,每个任务有10个训练周期用于训练。
●每种方法的训练模型都要花费~20分钟。(Tesla T4)
●每种方法的训练模型都要花费~60分钟。(Tesla K80)
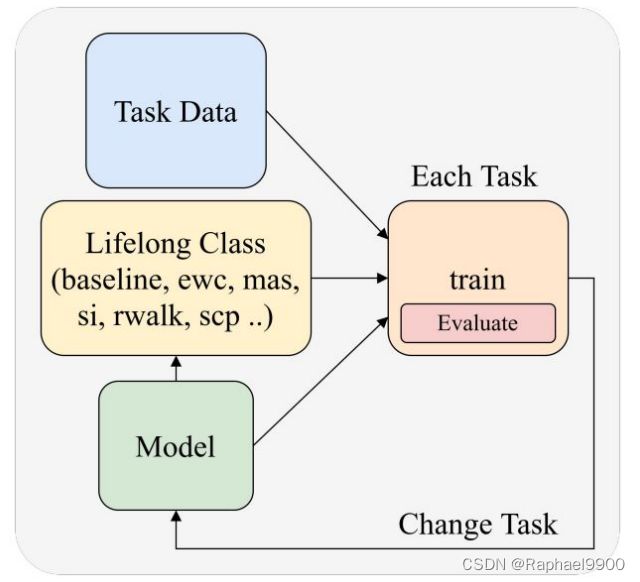
示例代码-指南:●实用工具●准备数据●准备模型●训练和评估●方法●图函数
示例代码-准备数据
●准备数据:○旋转和转换○Dataloaders and Arguments○可视化

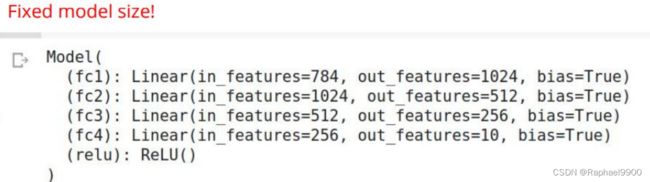
模型体系结构
样本代码-训练和评估
●训练:○顺序训练。○添加正则化项并更新它。
●评估:○使用特殊metric。
Training Pipeline:
MAS - Memory Aware Synapse
SI
SCP - Sliced Cramer Preservation

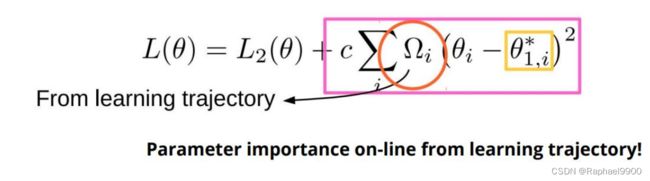
提出基于分布式的距离,以防止快速不妥协,避免高估参数的重要性。

二、实验
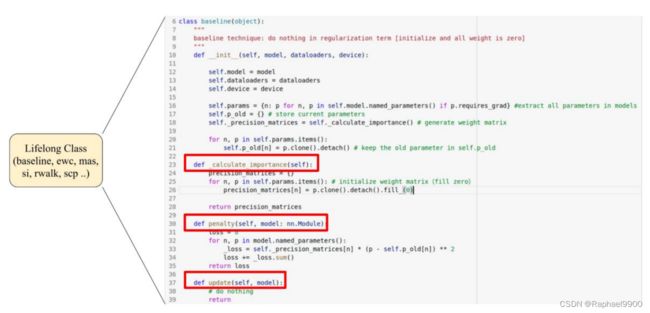
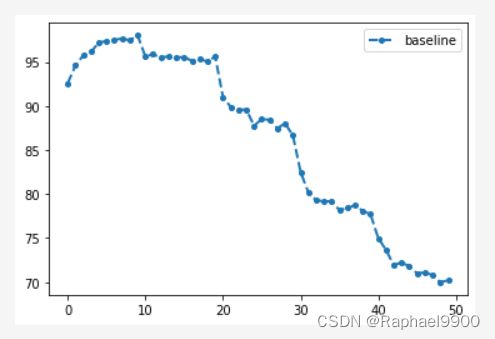
1、baseline
没有加入正则化项
# Baseline
class baseline(object):
"""
baseline technique: do nothing in regularization term [initialize and all weight is zero]
"""
def __init__(self, model, dataloader, device):
self.model = model
self.dataloader = dataloader
self.device = device
# extract all parameters in models
self.params = {n: p for n, p in self.model.named_parameters() if p.requires_grad}
# store current parameters
self.p_old = {}
# generate weight matrix
self._precision_matrices = self._calculate_importance()
for n, p in self.params.items():
# keep the old parameter in self.p_old
self.p_old[n] = p.clone().detach()
def _calculate_importance(self):
precision_matrices = {}
# initialize weight matrix(fill zero)
for n, p in self.params.items():
precision_matrices[n] = p.clone().detach().fill_(0)
return precision_matrices
def penalty(self, model: nn.Module):
loss = 0
for n, p in model.named_parameters():
_loss = self._precision_matrices[n] * (p - self.p_old[n]) ** 2
loss += _loss.sum()
return loss
def update(self, model):
# do nothing
return
# Baseline
print("RUN BASELINE")
model = Model()
model = model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=args.lr)
# initialize lifelong learning object (baseline class) without adding any regularization term.
lll_object=baseline(model=model, dataloader=None, device=device)
lll_lambda=0.0
baseline_acc=[]
task_bar = tqdm.auto.trange(len(train_dataloaders),desc="Task 1")
# iterate training on each task continually.
for train_indexes in task_bar:
# Train each task
model, _, acc_list = train(model, optimizer, train_dataloaders[train_indexes], args.epochs_per_task,
lll_object, lll_lambda, evaluate=evaluate,device=device, test_dataloaders=test_dataloaders[:train_indexes+1])
# get model weight to baseline class and do nothing!
lll_object=baseline(model=model, dataloader=train_dataloaders[train_indexes],device=device)
# new a optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=args.lr)
# Collect average accuracy in each epoch
baseline_acc.extend(acc_list)
# display the information of the next task.
task_bar.set_description_str(f"Task {train_indexes+2:2}")
# average accuracy in each task per epoch!
print(baseline_acc)
print("==================================================================================================")
[92.58999999999999, 94.64, 95.77, 96.13000000000001, 97.14, 97.41, 97.47, 97.64, 97.45, 98.00999999999999, 95.545, 95.76, 95.52000000000001, 95.64999999999999, 95.43, 95.61999999999999, 95.145, 95.355, 95.135, 95.52000000000001, 91.06666666666668, 89.78, 89.38333333333333, 89.49000000000001, 87.72666666666667, 88.55333333333334, 88.09333333333332, 87.38666666666667, 87.83333333333333, 86.75, 82.02000000000001, 79.6725, 79.28, 79.135, 79.34750000000001, 78.0925, 78.6275, 78.995, 78.17, 78.01249999999999, 74.888, 73.388, 71.65, 72.104, 71.682, 70.146, 70.874, 70.81200000000001, 69.728, 70.256]
2、EWC
ewc类应用EWC算法来计算正则项。我们想让我们的模型连续学习10个任务。这里我们展示了一个简单的例子,让模型连续学习两个任务(任务A和任务B)。在EWC算法中,损失函数的定义如下所示:
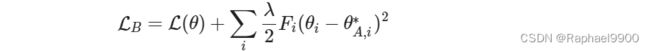
假设我们有一个具有两个以上参数的神经网络。Fi对应于第i护卫。F的定义如下所示:
![]()
我们只取矩阵的对角线值来近似每个参数的Fi。
# EWC
class ewc(object):
"""
@article{kirkpatrick2017overcoming,
title={Overcoming catastrophic forgetting in neural networks},
author={Kirkpatrick, James and Pascanu, Razvan and Rabinowitz, Neil and Veness, Joel and Desjardins, Guillaume and Rusu, Andrei A and Milan, Kieran and Quan, John and Ramalho, Tiago and Grabska-Barwinska, Agnieszka and others},
journal={Proceedings of the national academy of sciences},
year={2017},
url={https://arxiv.org/abs/1612.00796}
}
"""
def __init__(self, model, dataloader, device, prev_guards=[None]):
self.model = model
self.dataloader = dataloader
self.device = device
# extract all parameters in models
self.params = {n: p for n, p in self.model.named_parameters() if p.requires_grad}
# initialize parameters
self.p_old = {}
# save previous guards
self.previous_guards_list = prev_guards
# generate Fisher (F) matrix for EWC
self._precision_matrices = self._calculate_importance()
# keep the old parameter in self.p_old
for n, p in self.params.items():
self.p_old[n] = p.clone().detach()
def _calculate_importance(self):
precision_matrices = {}
# initialize Fisher (F) matrix(all fill zero)and add previous guards
for n, p in self.params.items():
precision_matrices[n] = p.clone().detach().fill_(0)
for i in range(len(self.previous_guards_list)):
if self.previous_guards_list[i]:
precision_matrices[n] += self.previous_guards_list[i][n]
self.model.eval()
if self.dataloader is not None:
number_data = len(self.dataloader)
for data in self.dataloader:
self.model.zero_grad()
# get image data
input = data[0].to(self.device)
# image data forward model
output = self.model(input)
# Simply use groud truth label of dataset.
label = data[1].to(self.device)
# generate Fisher(F) matrix for EWC
loss = F.nll_loss(F.log_softmax(output, dim=1), label)
loss.backward()
for n, p in self.model.named_parameters():
# 获取每个参数的梯度并求平方,然后在所有验证集中求平均值。
precision_matrices[n].data += p.grad.data ** 2 / number_data
precision_matrices = {n: p for n, p in precision_matrices.items()}
return precision_matrices
def penalty(self, model: nn.Module):
loss = 0
for n, p in model.named_parameters():
# generate the final regularization term by the ewc weight (self._precision_matrices[n]) and the square of weight difference ((p - self.p_old[n]) ** 2).
_loss = self._precision_matrices[n] * (p - self.p_old[n]) ** 2
loss += _loss.sum()
return loss
def update(self, model):
# do nothing
return
lll_lambda=100
[92.49000000000001, 94.62, 95.6, 96.17, 96.67, 97.21, 97.26, 97.48, 97.72, 97.78, 95.57, 96.035, 95.72, 95.88499999999999, 95.725, 95.795, 95.22, 95.275, 95.565, 95.46, 91.23666666666666, 89.55666666666667, 89.07333333333334, 88.04666666666667, 88.28999999999999, 87.44666666666667, 87.19999999999999, 87.97666666666667, 87.0, 87.14, 82.29250000000002, 80.735, 80.35749999999999, 80.8175, 80.7775, 79.1975, 80.59750000000001, 79.66250000000001, 79.62, 80.5825, 74.80399999999999, 74.07600000000001, 73.082, 72.012, 70.48400000000001, 71.848, 72.344, 72.29599999999999, 71.736, 71.37]
3、MAS
class mas(object):
"""
@article{aljundi2017memory,
title={Memory Aware Synapses: Learning what (not) to forget},
author={Aljundi, Rahaf and Babiloni, Francesca and Elhoseiny, Mohamed and Rohrbach, Marcus and Tuytelaars, Tinne},
booktitle={ECCV},
year={2018},
url={https://eccv2018.org/openaccess/content_ECCV_2018/papers/Rahaf_Aljundi_Memory_Aware_Synapses_ECCV_2018_paper.pdf}
}
"""
def __init__(self, model: nn.Module, dataloader, device, prev_guards=[None]):
self.model = model
self.dataloader = dataloader
# extract all parameters in models
self.params = {n: p for n, p in self.model.named_parameters() if p.requires_grad}
# initialize parameters
self.p_old = {}
self.device = device
# save previous guards
self.previous_guards_list = prev_guards
# generate Omega(Ω) matrix for MAS
self._precision_matrices = self.calculate_importance()
# keep the old parameter in self.p_old
for n, p in self.params.items():
self.p_old[n] = p.clone().detach()
def calculate_importance(self):
precision_matrices = {}
# initialize Omega(Ω) matrix(all filled zero)
for n, p in self.params.items():
precision_matrices[n] = p.clone().detach().fill_(0)
for i in range(len(self.previous_guards_list)):
if self.previous_guards_list[i]:
precision_matrices[n] += self.previous_guards_list[i][n]
self.model.eval()
if self.dataloader is not None:
num_data = len(self.dataloader)
for data in self.dataloader:
self.model.zero_grad()
output = self.model(data[0].to(self.device))
################################################################
##### TODO: generate Omega(Ω) matrix for MAS. #####
l2_norm = output.norm(2, dim=1).pow(2).mean()
l2_norm.backward()
for n, p in self.model.named_parameters():
# get the gradient of each parameter and square it, then average it in all validation set.
precision_matrices[n].data += p.grad.data ** 2 / num_data
################################################################
precision_matrices = {n: p for n, p in precision_matrices.items()}
return precision_matrices
def penalty(self, model: nn.Module):
loss = 0
for n, p in model.named_parameters():
_loss = self._precision_matrices[n] * (p - self.p_old[n]) ** 2
loss += _loss.sum()
return loss
def update(self, model):
# do nothing
return
4、SI
# SI
class si(object):
"""
@article{kirkpatrick2017overcoming,
title={Overcoming catastrophic forgetting in neural networks},
author={Kirkpatrick, James and Pascanu, Razvan and Rabinowitz, Neil and Veness, Joel and Desjardins, Guillaume and Rusu, Andrei A and Milan, Kieran and Quan, John and Ramalho, Tiago and Grabska-Barwinska, Agnieszka and others},
journal={Proceedings of the national academy of sciences},
year={2017},
url={https://arxiv.org/abs/1612.00796}
}
"""
def __init__(self, model, dataloader, epsilon, device):
self.model = model
self.dataloader = dataloader
self.device = device
self.epsilon = epsilon
# extract all parameters in models
self.params = {n: p for n, p in self.model.named_parameters() if p.requires_grad}
self._n_p_prev, self._n_omega = self._calculate_importance()
self.W, self.p_old = self._init_()
def _init_(self):
W = {}
p_old = {}
for n, p in self.model.named_parameters():
n = n.replace('.', '__')
if p.requires_grad:
W[n] = p.data.clone().zero_()
p_old[n] = p.data.clone()
return W, p_old
def _calculate_importance(self):
n_p_prev = {}
n_omega = {}
if self.dataloader != None:
for n, p in self.model.named_parameters():
n = n.replace('.', '__')
if p.requires_grad:
# Find/calculate new values for quadratic penalty on parameters
p_prev = getattr(self.model, '{}_SI_prev_task'.format(n))
W = getattr(self.model, '{}_W'.format(n))
p_current = p.detach().clone()
p_change = p_current - p_prev
omega_add = W/(p_change**2 + self.epsilon)
try:
omega = getattr(self.model, '{}_SI_omega'.format(n))
except AttributeError:
omega = p.detach().clone().zero_()
omega_new = omega + omega_add
n_omega[n] = omega_new
n_p_prev[n] = p_current
# Store these new values in the model
self.model.register_buffer('{}_SI_prev_task'.format(n), p_current)
self.model.register_buffer('{}_SI_omega'.format(n), omega_new)
else:
for n, p in self.model.named_parameters():
n = n.replace('.', '__')
if p.requires_grad:
n_p_prev[n] = p.detach().clone()
n_omega[n] = p.detach().clone().zero_()
self.model.register_buffer('{}_SI_prev_task'.format(n), p.detach().clone())
return n_p_prev, n_omega
def penalty(self, model: nn.Module):
loss = 0.0
for n, p in model.named_parameters():
n = n.replace('.', '__')
if p.requires_grad:
prev_values = self._n_p_prev[n]
omega = self._n_omega[n]
_loss = omega * (p - prev_values) ** 2
loss += _loss.sum()
return loss
def update(self, model):
for n, p in model.named_parameters():
n = n.replace('.', '__')
if p.requires_grad:
if p.grad is not None:
self.W[n].add_(-p.grad * (p.detach() - self.p_old[n]))
self.model.register_buffer('{}_W'.format(n), self.W[n])
self.p_old[n] = p.detach().clone()
return
5、RWalk
6、SCP
def sample_spherical(npoints, ndim=3):
vec = np.random.randn(ndim, npoints)
vec /= np.linalg.norm(vec, axis=0)
return torch.from_numpy(vec)
class scp(object):
"""
OPEN REVIEW VERSION:
https://openreview.net/forum?id=BJge3TNKwH
"""
def __init__(self, model: nn.Module, dataloader, L: int, device, prev_guards=[None]):
self.model = model
self.dataloader = dataloader
self.params = {n: p for n, p in self.model.named_parameters() if p.requires_grad}
self._state_parameters = {}
self.L= L
self.device = device
self.previous_guards_list = prev_guards
self._precision_matrices = self.calculate_importance()
for n, p in self.params.items():
self._state_parameters[n] = p.clone().detach()
def calculate_importance(self):
precision_matrices = {}
for n, p in self.params.items():
precision_matrices[n] = p.clone().detach().fill_(0)
for i in range(len(self.previous_guards_list)):
if self.previous_guards_list[i]:
precision_matrices[n] += self.previous_guards_list[i][n]
self.model.eval()
if self.dataloader is not None:
num_data = len(self.dataloader)
for data in self.dataloader:
self.model.zero_grad()
output = self.model(data[0].to(self.device))
mean_vec = output.mean(dim=0)
L_vectors = sample_spherical(self.L, output.shape[-1])
L_vectors = L_vectors.transpose(1,0).to(self.device).float()
total_scalar = 0
for vec in L_vectors:
scalar=torch.matmul(vec, mean_vec)
total_scalar += scalar
total_scalar /= L_vectors.shape[0]
total_scalar.backward()
for n, p in self.model.named_parameters():
precision_matrices[n].data += p.grad**2 / num_data
precision_matrices = {n: p for n, p in precision_matrices.items()}
return precision_matrices
def penalty(self, model: nn.Module):
loss = 0
for n, p in model.named_parameters():
_loss = self._precision_matrices[n] * (p - self._state_parameters[n]) ** 2
loss += _loss.sum()
return loss
def update(self, model):
# do nothing
return