【Causality】因果图入门
这部分主要讲了causal discovery的算法描述和图论相关表达。下一篇会整理intervention相关的理论,欢迎大家一起学习。
因果图入门
- 初始因果发现
-
- 因果发现问题
- 因果发现算法
- 因果图模型的相关定义
-
- 因果图
- 因果边假设
- 结构因果模型
- 马尔可夫性
- D-faithfulness
- D-separation
- CPDAG
- Ancestral graph
- 下期预告
初始因果发现
了解系统中现象的规律实际上就是以因果的角度取建模变量间的内在联系。尤其在进行决策时,我们需要考虑干预(intervention)造成的潜在影响。实际上, 一个研究的主要目的往往都是在评估一个“动作”(action)的影响,而不是关联性。因此,因果研究的过程时,往往也是将决策的影响划分为因果影响和非因果影响的过程。
当因果图(causal graph)未知时,我们则尝试用数据和先验知识来重现因果对(cause-effect pairs)。这种学习带有因果解释性的图结构的过程就称为因果发现(causal discovery),是因果的一个分支,是从数据中辨别和评价因果效应并且用因果图呈现的学科。
因果图用一条从因指向果的箭头表达因果性,在表达上非常有效。与深度学习算法不同,因果学习是数据驱动的方法,具有无与伦比的可解释性,能够让研究者对研究问题有更深的理解。
因果发现问题
因果发现问题可以描述为为给定的数据寻找一个因果图作为可能的因果关系解释。数学语言表示为设 G G G为数据集 D D D的变量集 V V V定义的一个图结构集, G ∗ ∈ G G^* \in G G∗∈G是数据集 D D D生成的真实的但是未知的图。
因果发现算法
我们说一个算法可以解决(solve)一个因果发现问题当且仅当它能够在现有的数据集和先验知识的情况下可以收敛至(converge to)真实的图 G ∗ G^* G∗。对于因果发现算法有很多的描述。我们认为一个算法是sound的当他可以解决一个因果发现问题;它是complete的当它能够找到最具信息量的因果图。而一个图是最具信息量(most informative)的当且仅当在没有提供其他信息的情况下,该图未确定方向的边无法确定方向,已经确定方向的边无法更改方向。一个算法是具有一致性(consistent)的当它输出的图对应的概率分布总是与输入的数据一致;是具有可识别性(identifiable)的当它能够决定因果图任意边的方向。但这是比较困难的,一般的因果学习算法可以在马尔可夫等价类(markov equivalence class)层面具有可识别性,而马尔科夫等价类的具体表达为CPDAG,这些在定义部分都会阐释。
因果图模型的相关定义
因果图
因果图是由因果关系组成的图结构表达,这也是与贝叶斯网络不同的地方。颠倒贝叶斯网络中的一个边也许会得到相同的概率分布,对于贝叶斯网络来说没有区别。但是对于因果图来说则是彻底改变了因果机制(变量间的因果关系)
因果边假设
因果图中每个变量X的值完全由一个关于其父变量的函数决定:
X : = f ( P a ( x ) ) , ∀ X ∈ V X:= f(Pa(x)), \forall X \in V X:=f(Pa(x)),∀X∈V
结构因果模型
也称为结构方程模型,由一个元组 M = ( V , U , F , P ) M=(V,U,F,P) M=(V,U,F,P),其中:
- V V V是内生的变量,也称为可观测变量,
- U U U是外生的变量,也成为非观测变量,隐变量,显然 V ∩ U = ∅ V \cap U = \empty V∩U=∅,
- F F F是一个函数集,其中的方程 f ∈ F : ( V ∩ U ) p → V f \in F:(V \cap U)^p \rightarrow V f∈F:(V∩U)p→V,其中 p p p表示f的参数数量。
- P P P是外生变量的联合概率分布, P ( U ) = ∏ i P ( U i ) P(U) = {\textstyle \prod_{i}}P(U_i) P(U)=∏iP(Ui).
马尔可夫性
一个图具有马尔可夫性,或者说可以做概率因子分解,当其对应的联合概率分布可以被递归分解为:
P ( V ) = ∏ X ∈ V P ( X ∣ P a ( X ) ) P(V) = \prod_{X \in V}P(X|Pa(X)) P(V)=X∈V∏P(X∣Pa(X))
D-faithfulness
当概率的独立性可以由图的独立性表达时,我们称图具有D-faithfulness,即
X ⊥ P Y ∣ Z ⇒ X ⊥ G Y ∣ Z X\perp _PY|Z \Rightarrow X\perp_GY|Z X⊥PY∣Z⇒X⊥GY∣Z,
其中Z是 V ∖ X Y V \setminus XY V∖XY的子集。
D-separation
用于测试对于任意忠实于因果图G的概率P,在给定Z的情况下,X是否条件独立于Y。具体表现为Z阻断了所有X和Y之间的路径。路径主要有以下几种形式:
- X ← Z → Y X \leftarrow Z \rightarrow Y X←Z→Y是一个叉结构,
- X → Z → Y X \rightarrow Z \rightarrow Y X→Z→Y是一个链结构,
- X → Z ← Y X \rightarrow Z \leftarrow Y X→Z←Y是一个对撞结构。
另 π \pi π表示X到Y的一个路径,则 π \pi π会被Z阻断当 π \pi π包含了:
- 叉结构 X ← Z → Y X \leftarrow Z \rightarrow Y X←Z→Y或链结构 X → Z → Y X \rightarrow Z \rightarrow Y X→Z→Y且中间节点Z被观测,或
- 对撞结构 X → Z ← Y X \rightarrow Z \leftarrow Y X→Z←Y且中间节点Z及其子节点都未被观测。
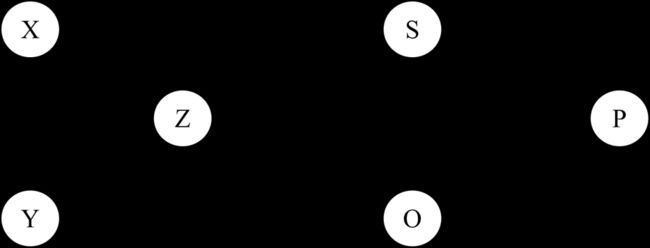
如下图所示,当Z未被观测时,X和Y是独立的。而X与S想实现条件独立,必须观测Z。
CPDAG
Partially DAG既包含了有向边(directed edge)又包含了非有向边(undirected edge)。因此,PDAG可以将因果对与未知的因果关系区别开。
Skeleton 是将PDAG所有有向边转化为非有向边后的产物。V-structure则是一个元组 X → Z ← Y X \rightarrow Z \leftarrow Y X→Z←Y,其中X与Y不相邻。在PDAG中,v-structure解码了概率分布的条件独立。不可反向边(compelled edge)是任意边满足当该边逆转方向时,会增加或删除v-structure。其他边则称为可逆转边(reversible edge)。
等价类(equivalence class)的性质是设置任意非有向边的方向都不会导致概率分布的变化。
Observational markov equivalence 是指两个DAG G和H图应有相同的seleton和v-structure,记作 G ≡ H G\equiv H G≡H,意味着改变可转向边的方向虽然导致了不同的机构但是具有相同的因子分解。此时G和H属于同一马尔可夫等价类。
Completed PDAG(CPDAG),也称作essential graph或者最大有向图, 是任意PDAG当所有的有向边都是不可反向边而所有非有向边都是可逆转边。CPDAG是马尔科夫等价类的通常表达。
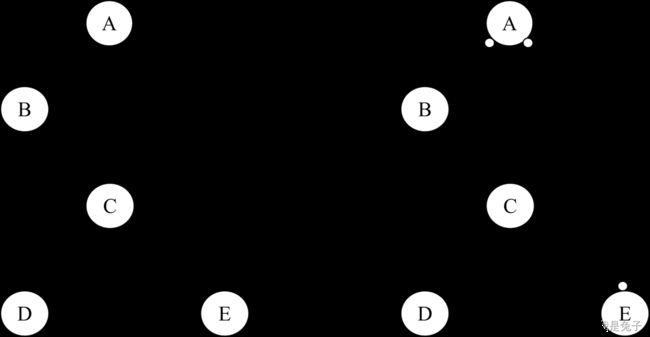
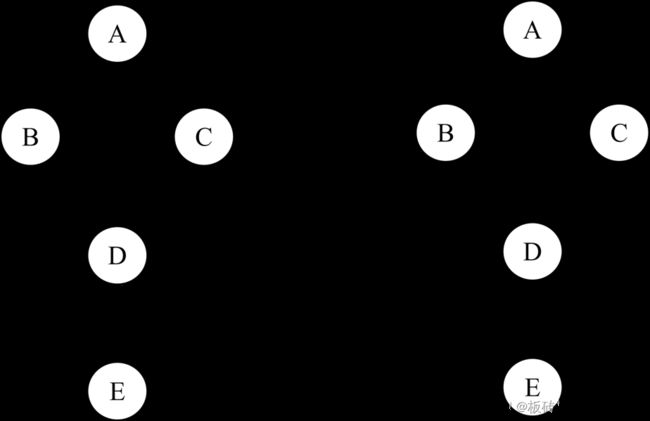
下图是一个有向图及其等价类图。其中 B → D ← C B\rightarrow D\leftarrow C B→D←C之间形成了对撞结构。 A → B A \rightarrow B A→B和 A → C A \rightarrow C A→C即使转变方向也不会出现新的v-structure,因此是可以转向边,需要变为undirected edge。 D → E D\rightarrow E D→E转变方向会出现新的v-structure B → D ← E B\rightarrow D \leftarrow E B→D←E和 C → D ← E C\rightarrow D \leftarrow E C→D←E,因此也是不可转向边(compelled edge),应为有向边。
Ancestral graph
混合图(Mixed graph)是包含有向边、无向边和双向边的图。双向边 X ↔ Y X\leftrightarrow Y X↔Y便是X是Y的一个对偶集合(节点),记作 X ∈ S p ( Y ) X \in Sp(Y) X∈Sp(Y)。混合图中,叉结构、链结构和对撞结构只有在双向边中才能修改。
M-separation是指对于混合图G中的一个路径 π \pi π和观测变量集V的子集Z, π \pi π被Z阻断当且仅当 π \pi π包含:
- 非对撞结构而中间变量被观测(包含在Z中),或者
- 对撞结构但中间变量或其子节点都未被观测。
我们称Z m-分离了X和Y当Z将所有连接X和Y的路径都阻断了。
祖先图(Ancestral graph)是一个无环混合图,且当有一个双向边连接了X和Y,那么X和Y之间就不存在其他的又向路径。
最大化祖先图(Maximal Ancestral graph)是一个祖先图当不相邻的节点间都是m-separated的。MAG的马尔可夫等价类由部分祖先图表示。对于等价类中的MAG,同一位置的标记一致相同,称为不变标记。
在混合图中我们不再关注边,而关注端点的标记。如一个 → \rightarrow →可以分解为尾标记(-)和一个箭头标记(>)。而部分祖先图(partial ancestral graph)是一个包含了尾标记(-),箭头(><)和圆标记(o)的图。将图G的等价类记作集合[G],那么
- G有与[G]相同的骨架(邻接矩阵),并且
- G中的尾标记和箭头标记都是不变标记。
根据上面两条,显然,PAG中圆标记也是不变的,因此,PAG也是MAG的马尔科夫等价类中最具信息量(most informative)的图,常用作表示MAG的马尔科夫等价类。因此与CPDAG一样满足complete的定义。
祖先图可以可能涉及潜在混杂因素和/或选择偏差的数据生成过程,而不明确地建模未观察变量。PAG的解释非常复杂:
- ( X → Y X \rightarrow Y X→Y):X导致了Y但Y没有导致X,X和Y之间可能有未被观测的干扰变量。
- ( X ↔ Y X \leftrightarrow Y X↔Y):X与Y之间没有因果关系且必存在一个未被观测的干扰变量同时为X和Y的父节点(因)。
- ( X ∘ → Y X \circ \rightarrow Y X∘→Y):两种情况:X导致了Y;X与Y之间没有因果关系且必存在一个未被观测的干扰变量同时为X和Y的父节点。
- ( X ∘ − ∘ Y X \circ -\circ Y X∘−∘Y):三种情况:X导致了Y;Y导致了X;X与Y之间没有因果关系且必存在一个未被观测的干扰变量同时为X和Y的父节点。
下期预告
关于因果图的图论基本内容就是这些了。下次更新intervention相关内容,包含前门后门准则、do-calculus等。笔者会先去看Causal Diagrams for Empirical Research这篇文章,希望一切顺利,mark~