【Causality】do calculus原理

这部分主要讲了causal discovery的do-calculus理论。这是将干预的结果概率化表达的重要理论，是评估因果作用的主要方法。欢迎大家一起学习

理论

1 有向图

相关图论知识请移步：

【Causality】因果图入门

2 do算子

通过因果之梯，我们知道，如果想要把对因果的理解上升到“干预”的层面，就必须引入“干预”。我们用do算子来在概率分布层面表述这种动作。在$DAG$中$do(X_i)=x_i^{\prime }$表示如下的操作：将$DAG$中指向$x_i$的有向边全部切断，且将$X_i$的取值固定为常数$x_i^{\prime }$ 。如此操作，得到的新$DAG$的联合分布可以记做$P(x_1,x_2,...,x_n|do(X_i)=x_i)$ 。 可以证明，干预后的联合分布为
$$P(x_1,...,x_n|do(X_i)=x_i^{\prime })=\frac{P(x_1,...,x_n)}{P(x_i|Pa(x_i))}I(x_i=x_i^{\prime })$$

3 do ≠ condition

如下图（1）所示，当$x_1$是$x_2$的原因（父节点）时，$P(X_2=x_2|X_1=x_1)=P(X_2=x_2|do(X_1)=x_1)$，因为在干预前，原因的状态原本就对应着相应的结果状态，改变原因的值不会影响这种对应关系。

但如图（2）所示，当$x_1$是$x_2$的结果（子节点），给定了结果，对应的原因状态的可能性是不变的，即人为的干预结果，并不影响原因的分布，所以$$P(X_2=x_2|X_1=x_1)\ne P(X_2=x_2|do(X_1)=x_1)=P(X_2=x_2)$，根据因果边假设（causal edge assumption），从图像上来看，指向X_1的所有边都被删除了。

4 后门准则与The Adjustment Formula （校正公式）

根据 do 算子，便可以定义因果作用。比如二值的变量$Z$对于$Y$的平均因果作用（average causal effect）定义为
$$ACE(Z\to Y)=E\left\{Y|do(Z=1)\right\}-E\left\{Y|do(Z=0)\right\}$$
也就是激活$Z$与不激活$Z$之间的区别。

“可识别性” 这个概念将被频繁的使用。因果推断中的识别性，和传统统计中的识别性定义是一致的。统计中，如果两个不同的模型参数，对应不同的观测数据的分布，那么我们称模型的参数可以识别。这里，如果因果作用可以用观测数据的分布唯一的表示，那么我们称因果作用是可以识别的。

有关$D$-分离的概念请看图论。

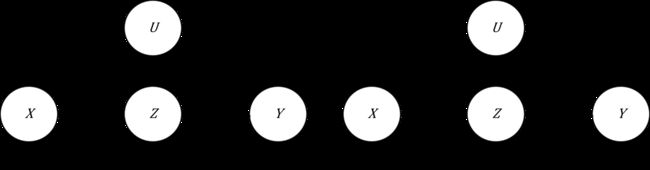
后门准则：如图(1)，在$DAG$中，如果如下条件满足：

1. $Z$中节点不是$X$的后代；
2. $Z$阻断了$(X,Y)$之间所有指向$X$的路径（又称为后门路径），

则称变量集合$Z$相对于变量有序对$(X，Y)$满足后门准则。且Pearl（1995）证明，若存在一个变量集合$Z$相对于$(X,Y)$满足后门准则，那么$X$到$Y$的因果作用是可以识别的。进行干预后，我们会得到新的图称作manipulated model，见图(2)，对应的概率记作$P_m$.

根据后门准则，有

1. $P_m(Z=z)=P(Z=z)$
2. $P_m(Y=y|X=x,Z=z)=P(Y=y|X=x,Z=z)$

因此，校正公式（又称作causal effect rule）得以满足，如下：
$$\begin{array}{rl}P(Y=y|do(X)=x)& =\sum _{z}P(Y=y,Z=z|do(X=x))\\ & =\sum _{z}P(Y=y|X=x,Z=z)P(Z=z)\\ & =\sum _{z}P(Y=y|X=x,Pa(x)=z)P(Pa(x)=z)\end{array}$$

与$ACE$识别公式相同，用$Z$做调整，在分层加权求和求期望。

后门准则的例子（转载）

https://zhuanlan.zhihu.com/p/395623955

后门准则失败的例子

5 前门准则与The Adjustment Formula （校正公式）

前门准则：如图(1)，在$DAG$中，如果满足下列条件：

1. $Z$切断了所有$X$到$Y$的直接路径
2. $X$到$Z$没有后门路径
3. 所有$Z$到$Y$的后门路径都被$X$阻断。

如图，$P(Y=y|X=x)$可以分解为两个后门$P(Y=y|Z=z)$和$P(Z=z|X=x)$。
对于$P(Y=y|Z=z)$，满足后门准则的变量有$\left\{X\right\}$，所以根据后门准则，
$$P(Y=y|Z=z)=\sum _{x^{\prime }}P(Y=y|Z=z,X=x^{\prime })P(X=x^{\prime })$$
对于$P(Z=z|X=x)$，没有满足后门准则的变量，因此不变。则有
$$\begin{array}{rl}P(Y=y|do(X)=x)& =\sum _{z}P(Y=y,Z=z|do(X=x))\\ & =\sum _{z}P(Y=y|Z=z,do(X)=x)P(Z=z|do(X)=x)\\ & =\sum _{z}P(Y=y|do(Z=z))P(Z=z|do(X)=x)\\ & =\sum _z\sum _{x^{\prime }}P(Y=y|Z=z,X=x^{\prime })P(X=x^{\prime })P(Z=z|X=x)\end{array}$$
进而得到前门准则的校正公式为
$$P(y|do(x))=\sum _{z}P(z|x)\sum _{x^{\prime }}P(y|x^{\prime },z)P(x^{\prime })$$
这两个准则的意义在于：（1）某些研究中，即使$DAG$中的某些变量不可观测，我们依然可以从观测数据中估计出某些因果作用；（2）这两个准则有助于我们鉴别“混杂变量” 和设计观察性研究。

6 do calculus

6.1 基本术语

1. $G_{\overline{X}}$：移除$G$中所有指向$X$的边，即$X$没有parent,也表示do(x)为空集；
2. $G_{\underline{X}}$：移除$G$中所有从$X$指出的边，即$X$没有；descendant
3. $G_{\overline{Z(W)}}$：移除$Z$指向$W$的所有边，即$Z$中没有$W$的parent。
4. $A\perp B|C$指已知C的情况下A条件独立于B。

6.2 三条规则

1. Ignoring observations（d-separation）：如果$G_{\overline{X}}$中$Y\perp Z|X,W$。
   $$P(y|do(x),z,w)=P(y|do(x),w)$$
2. Intervention/observation exchange（后门调整）：如果$G_{\overline{X},\underline{Z}}$中$Y\perp Z|X,W$，
   $$P(y|do(x),do(z),w)=P(y|do(x),z,w)$$
3. Ignoring interventions：如果$G_{\overline{X,Z(W)}}$中$Y\perp Z|X,W$，即$Y$和$Z$被$W$ $D$-separation。
   $$P(y|do(x),do(z),w)=P(y|do(x),w)$$

6.3 例子：计算$P(c|do(s))$

$$\begin{array}{cc}\begin{array}{rl}P(c|do(s))& =\sum _{t}P(c,t|do(s))\\ & =\sum _{t}P(c|t,do(s))P(t|do(s))\\ & =\sum _{t}P(c|do(t),do(s))P(t|s)\\ & =\sum _{t}P(c|do(t))P(t|s)\\ & =\sum _t\sum _{s^{\prime }}P(c|do(t),s^{\prime })P(s^{\prime }|do(t))P(t|s)\\ & =\sum _t\sum _{s^{\prime }}P(c|t,s^{\prime })P(s^{\prime }|do(t))P(t|s)\\ & =\sum _t\sum _{s^{\prime }}P(c|t,s^{\prime })P(s^{\prime })P(t|s)\end{array}& \begin{array}{rl}& 1行.边缘分布公式\\ & 2行.因子分解\\ & 3，4行.do(s)=空集，所以do(s)=s\\ & 5行.t和c后门被S阻断，因为T\leftarrow S\leftarrow G\to C，根据后门修正公式\\ & 6行.t是c的原因，改变t不会影响c对应的分布，还是原本的条件分布\\ & 7行.t是s的结果，人为干预结果不会影响原因的分布，因此do(t)与s无关\end{array}\end{array}$$

下期预告

接下来会用代码实现do-calculus的计算，大概就这两天。