Deep Stable Learning for Out-Of-Distribution Generalization

简介

 这是一篇来自2021年CVPR的论文。文章的主要贡献就是通过给每个样本加权，来消除掉虚假关联，使得模型更加关注与分类结果有因果关系的discriminative features。举一个简单的例子，下图是传统的resnet18网络和作者的stableNet对图片中不同特征的关注差异，stableNet会更关注狗本身的特征，它是与标签dog有因果关系的特征，而resnet的关注点还会有背景，如水，它把水也作为dog的特征（因为使用的训练集大部分是以水为背景的），而文章的目标就是消除这样的虚假关联。
 那么文章的题目叫做for out-of-distribution generalization，它主要是应用在泛化任务中，即训练数据集和测试数据集分布有迁移shift。分布发生转移，与标签有因果关系的特征是不会变的，如下图中狗的特征，造成泛化任务识别准确率降低的原因是不同分布伪相关特征confounder的不同，如背景水。这两类特征都会对预测结果产生影响，并且它们相互纠缠，作者提出的一系列方法就是让这两类特征独立，然后让网络学习到哪些特征与预测结果是因果关系以及它们对结果影响的大小，那么无论分布怎么转移，网络都能做出稳定预测了。强烈建议先看一下文末视频，肯定要比我讲得清楚。

网络架构

 下图是论文中的网络结构图。结构图下面一路就是常规的分类网络，可以是resnet18可以是densenet都可以，那么它与常见的分类网络唯一的不同之处在于上面一路为每个样本加权，先通过RFF方法增广Feature Map，然后通过LSWD一套算法为每个样本学习一个权重，这个权重就加在网络输出的预测和标签的交叉熵上，最后对每个样本的交叉熵累加作为损失函数。（常规损失函数每个样本交叉熵的权值可以看作是1）

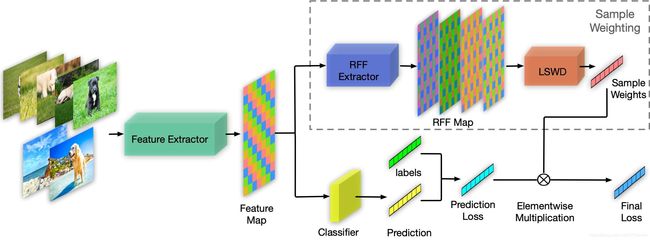
关键部分

 样本加权

 要消除不同特征之间的关联，为什么要给每个样本加权？我最初也有这样的疑惑。按照作者的解释，确实应该给特征向量的每一维都加权，每一个样本也要加权，才能保证把特征的任一维作为‘实验组’，其他‘对照组’服从相同分布，但这样一来会有$k\ast N$个参数($k$为特征维度，$N$为样本数)，计算开销太大，其次没有相应理论支撑。于是作者做了一个让步，只对样本加权，实验证明效果也挺好，所以可能就这样了。。。

 Independence testing statistics

 这就是使用核方法为两个变量的独立性提供一种度量，后面把这种度量发展成为了文章的损失函数。根据作者给出的参考文献顺藤摸瓜，就会发现这类方法研究内容也比较相似，发表时间大多在04-08年，比较理论比较数学，暂时不展开了，后面必要再补充。那么大概的过程是这样的：参考文献【14】最先给出了互协方差因子的定义：$<h_A,{\Sigma }_{AB}\cdot h_B>=E_{AB}[h_A(A)\cdot h_B(B)]-E_A[h_A(A)]\cdot E_B[h_B(B)]$；参考文献【20】提出HSIC方法，并给出一个定理要想A、B独立只需${\Sigma }_{AB}=0$，即$\Sigma =0$ ⇔$A$⊥$B$。那么$\Sigma =0$就可以作为一个准则criterion来监督特征解耦，就是可以作为损失函数；接着参考文献【61】就提出利用随机傅里叶特征RFF来近似基于核方法的条件独立性测试，这个方法的优点就是速度快准确率也不差。原文给出的partial cross-covariance matrix是基于条件概率的，作者在这里应该是做了推广，那么就有了最终的独立性测试以及损失函数，直接论文截图了：

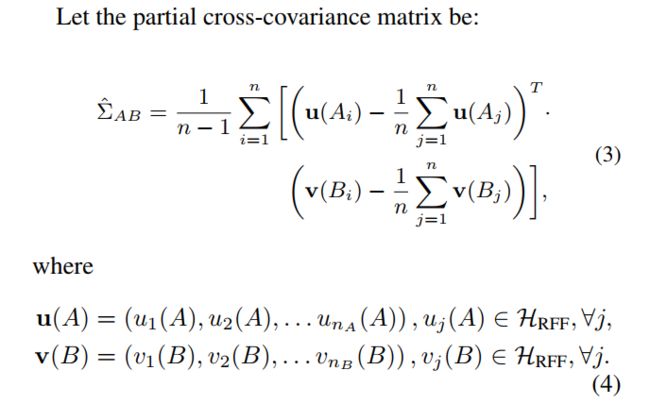
 Learning sample weights for decorrelation

  那么加权方法就是每个样本RFF映射函数的值*权重$w$，如下：

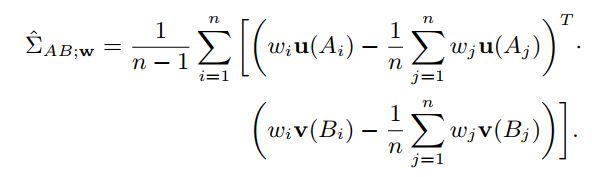
 $w$的优化函数如下：

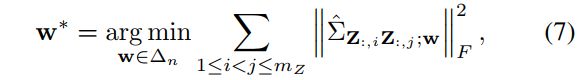
 这里就有点疑惑：$i,j$的取值范围怎么是$[1,mz]$？$mz$是特征向量的维度呀！还有就是我觉得${\Sigma }_{AB}$应该衡量的是特征向量不同维度的独立性，而不是不同样本的独立性，不知道大家是否有相同疑问。则篇文章小毛病如缺个句号多个逗号也很常见。。。

 保存/重载学习全局权重

 设计这个方法还是因为算法空间/时间复杂度为$O(n^2)$，随着$n$规模增加会爆炸，另外现在的优化算法都是一个batch地取数据，也不便于得到global weights。
 对于这部分的理解也只能来源于论文，既没有参考文献也没有源码，只有论文描述。训练的过程中把之前所有的样本权重和特征向量都存起来，训练下一个batch时把之前保存内容都重载，拼接成一个全局的特征向量和权重，length为$k\ast B$，$k$取值0，1，2…为第$k$个batch，$B$为batchsize大小。这样看来计算复杂度会随着$k$的增加而增加。拼接特征向量为$$Z_o=Concat(Z_{G1},Z_{G2},...,Z_{Gk},Z_l)$$，同样拼接权重$$w_o=Concat(w_{G1},w_{G2},...,w_{Gk},w_l)$$G下标表示Global，参数固定不更新，l下表指代local，需要更新参数。在每个batch训练结束后，新的Global权重按下式生成：$$Z_{Gi}^{{}^{\prime }}={\alpha }_i{Z}_{Gi}+(1-{\alpha }_i)Z_L$$同理$w^{{}^{\prime }}$,设计${\alpha }_i$是考虑"记忆"?调节${\alpha }_i$大小可以调节记忆长短?

实验

 实验部分作者设计了4种由易到难的实验设置。最简单的classic，常规泛化任务设置，不同的域数据量相当。其次是unbalanced，它要求来自不同域的数据量按一定比例如5:1:1，来模拟未知数据分布的情形。然后是unbalanced+flexible，它是模拟这样一种情形：如狗和鸟两类，狗可以在草地上在水里面，但是狗不可以在树上，而鸟可以；不同类之间分布会有差异，但就实际附录中设置二和三看不出差别，可能是设置二每一类的图片情况未具体展开，而差别就在这里。最后是+adversarial，它是给不同类别的图片替换上相同的背景，人为给标签和域建立伪相关，难度确实挺大的。但是从实验是准确率以及saliency maps上看，作者的这套方法还挺有效。

附录

  附录部分主要是我自己在读文献的时候查阅的各种来源的资料，正文没解释清楚的地方可以参考附录内容

随机傅里叶特征RFF

 RFF干了一件什么样的事呢？简单来说，RFF将两条原始数据 $x,y$ 通过显式的映射函数 $Z$ 将其映射到一个低维的欧几里得空间 $R^D$ ，即$Z:R^d\to R^D$ ，并且映射后的两点内积就是核函数 $k(x,y)$的估计值：
$k(x,y)=<\varphi (x),\varphi (y)>\approx Z(x{)}^T\cdot Z(y)$
  不同于核函数 $k(\cdot ,\cdot )$对应的特征映射 $\varphi (\cdot )$ 会将 $x$ 映射到很高维度， $Z(\cdot )$将 $x$ 映射到了一个较低维空间(注意"较低维"是相对于映射 $\varphi (\cdot )$ 而言，而不是原始数据的维度 $d$。因此，我们可以简单地用 $Z$ 对输入进行变换，然后应用线性的学习方法来近似非线性的学习算法。

随机傅里叶特征(Random Fourier Features)
随机傅里叶特征方法简述(Random Fourier Features, RFF)，这篇文章的讲解思路是最清楚的，还有matlab代码实现

再生核希尔伯特空间RKHS

A Story of Basis and Kernel - Part II: Reproducing Kernel Hilbert Space

协方差

从多个角度来理解协方差（covariance），非常直观地讲明白了协方差公式为什么这样定义

相关视频

 2021 CVPR 论文分享会|Session4:机器学习及多模态-哔哩哔哩，这个视频是直接讲这篇文章，背景、方法、实验、数据集都有涉及，就是时长只有20min，讲得粗略。
 Towards Explainable and Stable Prediction | 崔鹏-哔哩哔哩，这个视频是在本文所讲论文论文之前，崔鹏教授对他们工作的介绍，基本思想已经成型，介绍更详尽些。
 浙江大学助理教授况琨：因果推理和稳定学习-哔哩哔哩，这个视频是崔鹏团队的况琨老师讲的，也就是本文所讲文章的理论铺垫，最初提出全局样本加权思想文章对应的视频。
  其实文章背景如论文中的introduction、related works部分看视频了解的更快。