《PROTOTYPICAL CONTRASTIVE LEARNING OF UNSUPERVISED REPRESENTATIONS》学习笔记
PROTOTYPICAL CONTRASTIVE LEARNING
-
- 引言
- 方法
- 实验
-
- Low-shot classification
- 特征可视化
- 消融实验
引言
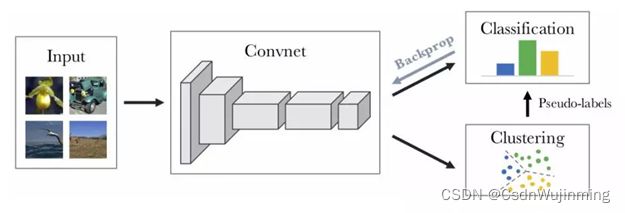
本文提出了一种无监督表征学习方法,主要针对对比损失(contrastive loss) 和聚类方法(deep cluster)方法改进,对比损失主要基于噪声对比估计(noise contrastive estimator),将同分布的embedding 拉近,不同分布的embedding距离推远。这些方法的主要问题是对比损失针对的实例判别任务只需浅层特征就可以处理,因为实验表明在10epochs内就可以达到很高精度,而继续训练只提供少量信息。而且提取的特征在下游任务中表现不好。所以实例对比学习到的特征缺少高层语义信息。另外对比损失需要构造大量负样本,而与正样本相似的负样本会损害表征学习。对于基于聚类的无监督学习方法,其结构如图1,重复 聚类-分类训练 的步骤,但cnn提取的特征还需要先pca降维,而且最后的分类器需要频繁初始化。
本文针对这些问题,结合InfoNCE 和EM(最大期望)算法改进deepcluster方法。聚类时,直接使用backbone的特征,将聚类中心作为一组相似样本的prototype(原型)特征,图2中蓝绿实心小圆,希望提取到的原型特征能包含一类样本共有的语义特征。如图2,实例对比损失的方法会将同实例的训练样本靠近,而本文的方法是将样本往聚类中心靠近。
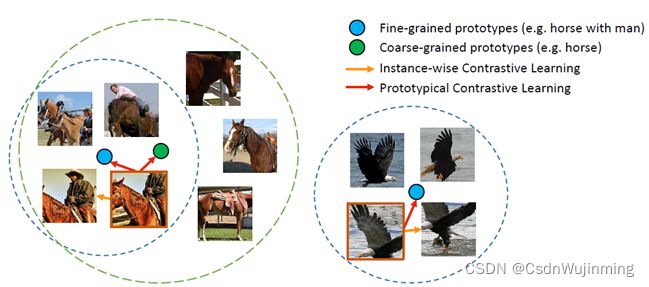
方法
目标函数使用似然函数,使用 θ \theta θ参数描述 p ( x i ; θ ) p(x_i;\theta) p(xi;θ),选择最优参数使得似然函数最大(已有样本发生可能性最大)。即公式 1 1 1:
θ ∗ = arg max θ ∑ i = 1 n log p ( x i ; θ ) (1) \theta^{*}=\underset{\theta}{\arg \max } \sum_{i=1}^{n} \log p\left(x_{i} ; \theta\right) \tag{1} θ∗=θargmaxi=1∑nlogp(xi;θ)(1)
引入隐变量 c i c_i ci,表示样本属于哪个原型特征对应的聚类中。公式1变为下式:
θ ∗ = arg max θ ∑ i = 1 n log p ( x i ; θ ) = arg max θ ∑ i = 1 n log ∑ c i ∈ C p ( x i , c i ; θ ) (2) \theta^{*}=\underset{\theta}{\arg \max } \sum_{i=1}^{n} \log p\left(x_{i} ; \theta\right)=\underset{\theta}{\arg \max } \sum_{i=1}^{n} \log \sum_{c_{i} \in C} p\left(x_{i}, c_{i} ; \theta\right) \tag{2} θ∗=θargmaxi=1∑nlogp(xi;θ)=θargmaxi=1∑nlogci∈C∑p(xi,ci;θ)(2)
对于等式右边的项利用凹函数log的jensen不等式可以确定其下界
∑ i = 1 n log ∑ c i ∈ C p ( x i , c i ; θ ) = ∑ i = 1 n log ∑ c i ∈ C Q ( c i ) p ( x i , c i ; θ ) Q ( c i ) ≥ ∑ i = 1 n ∑ c i ∈ C Q ( c i ) log p ( x i , c i ; θ ) Q ( c i ) (3) \sum_{i=1}^{n} \log \sum_{c_{i} \in C} p\left(x_{i}, c_{i} ; \theta\right)=\sum_{i=1}^{n} \log \sum_{c_{i} \in C} Q\left(c_{i}\right) \frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)} \geq \sum_{i=1}^{n} \sum_{c_{i} \in C} Q\left(c_{i}\right) \log \frac{p\left(x_{i}, c_{i} ; \theta\right)}{Q\left(c_{i}\right)} \tag{3} i=1∑nlogci∈C∑p(xi,ci;θ)=i=1∑nlogci∈C∑Q(ci)Q(ci)p(xi,ci;θ)≥i=1∑nci∈C∑Q(ci)logQ(ci)p(xi,ci;θ)(3)
通过最大化下界来求解参数,求解过程即EM算法过程,当 Q ( c i ) Q(c_i) Q(ci)满足下式时下界最大,参考PCL。
Q ( c i ) = p ( c i ; x i , θ ) (4) Q\left(c_{i}\right)=p\left(c_{i} ; x_{i}, \theta\right) \tag{4} Q(ci)=p(ci;xi,θ)(4)
因为 Q ( c i ) Q(c_i) Q(ci)与 θ \theta θ无关,所以 ∑ i = 1 n ∑ c i ∈ C Q ( c i ) log Q ( c i ) \sum_{i=1}^{n} \sum_{c_{i} \in C} Q\left(c_{i}\right) \log Q\left(c_{i}\right) ∑i=1n∑ci∈CQ(ci)logQ(ci)为常数
θ ∗ = arg max θ ∑ i = 1 n log p ( x i ; θ ) = arg max θ ∑ i = 1 n ∑ c i ∈ C Q ( c i ) log p ( x i , c i ; θ ) − c o n s t = arg max θ ∑ i = 1 n ∑ c i ∈ C Q ( c i ) log p ( x i , c i ; θ ) = arg max θ ∑ i = 1 n ∑ c i ∈ C p ( c i ; x i , θ ) log p ( x i , c i ; θ ) (5) \theta^{*}=\underset{\theta}{\arg \max } \sum_{i=1}^{n} \log p\left(x_{i} ; \theta\right)=\underset{\theta}{\arg \max }\sum_{i=1}^{n} \sum_{c_{i} \in C} Q\left(c_{i}\right) \log p\left(x_{i}, c_{i} ; \theta\right)-const \\ = \underset{\theta}{\arg \max }\sum_{i=1}^{n} \sum_{c_{i} \in C} Q\left(c_{i}\right) \log p\left(x_{i}, c_{i} ; \theta\right) \\ =\underset{\theta}{\arg \max }\sum_{i=1}^{n} \sum_{c_{i} \in C} p\left(c_{i} ; x_{i}, \theta\right) \log p\left(x_{i}, c_{i} ; \theta\right)\tag{5} θ∗=θargmaxi=1∑nlogp(xi;θ)=θargmaxi=1∑nci∈C∑Q(ci)logp(xi,ci;θ)−const=θargmaxi=1∑nci∈C∑Q(ci)logp(xi,ci;θ)=θargmaxi=1∑nci∈C∑p(ci;xi,θ)logp(xi,ci;θ)(5)
现在问题是如何知道 Q ( c i ) = p ( c i ; x i , θ ) Q(c_i)=p\left(c_{i} ; x_{i}, \theta\right) Q(ci)=p(ci;xi,θ)与 p ( x i , c i ; θ ) p\left(x_{i}, c_{i} ; \theta\right) p(xi,ci;θ),在聚类完成后,我们就可以知道每个样本与哪个原型相关,属于哪个聚类中。用指示函数给出每个样本与原型的关系。
p ( c i ; x i , θ ) = 1 ( x i ∈ c i ) (6) p\left(c_{i} ; x_{i}, \theta\right)=\mathbb{1}\left(x_{i} \in c_{i}\right) \tag{6} p(ci;xi,θ)=1(xi∈ci)(6)
对于 p ( x i , c i ; θ ) p\left(x_{i}, c_{i} ; \theta\right) p(xi,ci;θ),使用概率公式转换, p ( c i ; θ ) p\left(c_{i} ; \theta\right) p(ci;θ)使用均匀分布。
p ( x i , c i ; θ ) = p ( x i ; c i , θ ) p ( c i ; θ ) = 1 k ⋅ p ( x i ; c i , θ ) (7) p\left(x_{i}, c_{i} ; \theta\right)=p\left(x_{i} ; c_{i}, \theta\right) p\left(c_{i} ; \theta\right)=\frac{1}{k} \cdot p\left(x_{i} ; c_{i}, \theta\right) \tag{7} p(xi,ci;θ)=p(xi;ci,θ)p(ci;θ)=k1⋅p(xi;ci,θ)(7)
p ( x i ; c i , θ ) p\left(x_{i} ; c_{i}, \theta\right) p(xi;ci,θ)采用高斯分布
p ( x i ; c i , θ ) = exp ( − ( v i − c s ) 2 2 σ s 2 ) / ∑ j = 1 k exp ( − ( v i − c j ) 2 2 σ j 2 ) (8) p\left(x_{i} ; c_{i}, \theta\right)=\exp \left(\frac{-\left(v_{i}-c_{s}\right)^{2}}{2 \sigma_{s}^{2}}\right) / \sum_{j=1}^{k} \exp \left(\frac{-\left(v_{i}-c_{j}\right)^{2}}{2 \sigma_{j}^{2}}\right) \tag{8} p(xi;ci,θ)=exp(2σs2−(vi−cs)2)/j=1∑kexp(2σj2−(vi−cj)2)(8)
综合上面公式,最后目标函数为:
θ ∗ = arg min θ ∑ i = 1 n − log exp ( v i ⋅ c s / ϕ s ) ∑ j = 1 k exp ( v i ⋅ c j / ϕ j ) (9) \theta^{*}=\underset{\theta}{\arg \min } \sum_{i=1}^{n}-\log \frac{\exp \left(v_{i} \cdot c_{s} / \phi_{s}\right)}{\sum_{j=1}^{k} \exp \left(v_{i} \cdot c_{j} / \phi_{j}\right)} \tag{9} θ∗=θargmini=1∑n−log∑j=1kexp(vi⋅cj/ϕj)exp(vi⋅cs/ϕs)(9)
因为要聚类,不知道需要多少个聚类数,所以聚类M次,每个聚类数为 k m k_m km,然后取平均,同时加上InfoNCE的Loss,最后总损失函数如下:
L ProtoNCE = ∑ i = 1 n − ( log exp ( v i ⋅ v i ′ / τ ) ∑ j = 0 r exp ( v i ⋅ v j ′ / τ ) + 1 M ∑ m = 1 M log exp ( v i ⋅ c s m / ϕ s m ) ∑ j = 0 r exp ( v i ⋅ c j m / ϕ j m ) ) (10) \mathcal{L}_{\text {ProtoNCE }}=\sum_{i=1}^{n}-\left(\log \frac{\exp \left(v_{i} \cdot v_{i}^{\prime} / \tau\right)}{\sum_{j=0}^{r} \exp \left(v_{i} \cdot v_{j}^{\prime} / \tau\right)}+\frac{1}{M} \sum_{m=1}^{M} \log \frac{\exp \left(v_{i} \cdot c_{s}^{m} / \phi_{s}^{m}\right)}{\sum_{j=0}^{r} \exp \left(v_{i} \cdot c_{j}^{m} / \phi_{j}^{m}\right)}\right) \tag{10} LProtoNCE =i=1∑n−(log∑j=0rexp(vi⋅vj′/τ)exp(vi⋅vi′/τ)+M1m=1∑Mlog∑j=0rexp(vi⋅cjm/ϕjm)exp(vi⋅csm/ϕsm))(10)
其中InfoNCE loss为
L InfoNCE = ∑ i = 1 n − log exp ( v i ⋅ v i ′ / τ ) ∑ j = 0 r exp ( v i ⋅ v j ′ / τ ) (11) \mathcal{L}_{\text {InfoNCE }}=\sum_{i=1}^{n}-\log \frac{\exp \left(v_{i} \cdot v_{i}^{\prime} / \tau\right)}{\sum_{j=0}^{r} \exp \left(v_{i} \cdot v_{j}^{\prime} / \tau\right)} \tag{11} LInfoNCE =i=1∑n−log∑j=0rexp(vi⋅vj′/τ)exp(vi⋅vi′/τ)(11) 参考Noise Contrastive Estimation和Contrastive Predictive Coding,注意里面构造的正负样本关系。
损失函数中有个 ϕ \phi ϕ参数,类似于温度系数,当聚类样本数越多越集中, ϕ \phi ϕ越小,这样样本间的相似度会放大,因此,紧密的簇( ϕ \phi ϕ 值小)相似度增大,松散的簇( ϕ \phi ϕ值大)相似度降低。同温度系数改变Loss,产生更平衡的cluster且其集中程度(concentration)相似。
实验
基于学习的特征在有限的微调下做后续任务
Low-shot classification
每个类别只有k个样本时的分类任务。ImageNet上无监督表征学习,在少样本中训练svm分类器。指标为mAP。参数设置同MoCo方法。
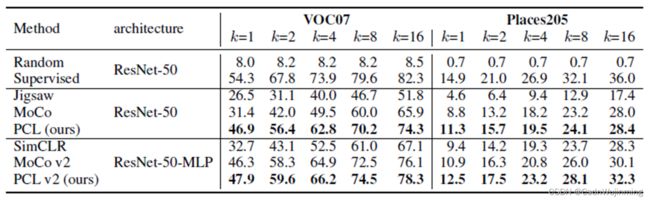
特征可视化
在ImageNet无监督训练完后,使用t-SNE工具可视化特征分布。对比MoCo方法

