人工智能笔记15 --贝叶斯网络
概述
什么是贝叶斯网络
• 贝叶斯网络是一种概率图模型
Ø 节点表示变量
Ø 有向边表示变量间的依赖关系
• 表达能力强、适用面广
Ø 专家系统知识表示 (80年代)
Ø 贝叶斯学习(90年代)
• 特点:先验推导后验
基础知识
定义1 统计概率
若在大量重复试验中,事件A发生的频率稳定地
接近于一个固定的常数 ρ \rho ρ,它表明事件A出现的可能性大小,则称此常数 ρ \rho ρ为事件A发生的概率,记为P(A), 即
ρ = P ( A ) \rho = P(A) ρ=P(A)
可见概率就是频率的稳定中心。任何事件A的概率为不大于1的非负实数,
0 < P ( A ) < 1 0
定义2 古典概率
我们设一种次试验有且仅有有限的N个可能结
果,即N个基本事件,而A事件包含着K个可能结果,则称K/N为事件A的概率,记为P(A)。即
P ( A ) = K / N P(A) = K/N P(A)=K/N
定义3 条件概率
我们把事件B已经出现的条件下,事件
A发生的概率记做为P(A|B)。并称为在B出现的条件下A出现的条件概率,而称P(A)为无条件概率。
若事件A与B中的任一个出现,并不影响另一事件出
现的概率,即当
P ( A ) = P ( A ⋅ B ) o r P ( B ) = P ( B ⋅ A ) P(A) = P(A\cdot B) \quad or\quad P(B) = P(B\cdot A) P(A)=P(A⋅B)orP(B)=P(B⋅A)
则称A与B是相互独立的事件
定理1 加法定理
两个不相容(互斥)事件之和的概率,等于两个事件概率之和,即P(A+B)=P(A)+P(B)两个互逆事件A和A-1的概率之和为1。即当A+A-1=Ω,且A与A-1互斥,则P(A)+P(A-1) =1,或常有P(A) =1-P(A-1) 。
若A、B为两任意事件,则P(A+B)=P(A)+P(B)-P(AB)
定理2 乘法定理
设A、B为两个不相容(互斥)非零事件,则其乘积的概率等于A和B概率的乘积,即
P ( A B ) = P ( A ) P ( B ) 或 P ( A B ) = P ( B ) P ( A ) P(AB)=P(A)P(B) 或 P(AB)=P(B) P(A) P(AB)=P(A)P(B)或P(AB)=P(B)P(A)
设A、B为两个任意的非零事件,则其乘积的概率等于A(或B)的概率与在A(或B)出现的条件下B(或A)出现
的条件概率的乘积。
P ( A ⋅ B ) = P ( A ) ⋅ P ( B ∣ A ) 或 P ( A ⋅ B ) = P ( B ) ⋅ P ( A ∣ B ) P(A·B)=P(A)·P(B|A) 或 P(A·B)=P(B)·P(A|B) P(A⋅B)=P(A)⋅P(B∣A)或P(A⋅B)=P(B)⋅P(A∣B)
(1) 先验概率
先验概率是指根据历史的资料或主观判断所确定的各事件发生的概率,该类概率没能经过实验证实,属于检验前的概率,所以称之为先验概率。先验概率一般分为两类,一是客观先验概率,是指利用过去的历史资料计算得到的概率;二是主观先验概率,是指在无历史资料或历史资料不全的时候,只能凭借人们的主观经
验来判断取得的概率
(2) 后验概率
后验概率一般是指利用贝叶斯公式,结合调查等方式获取了新的附加信息,对先验概率进行修正后得到的更符合实际的概率。
(3) 联合概率
联合概率也叫乘法公式,是指两个任意事件的乘积的概率,或称之为交事件的概率。
(4)全概率公式

熵(信息熵)反应了系统的不确定性
H = − ∑ i = 1 n P ( B i ) l o g 2 P ( B i ) H = -\sum^n_{i=1}P(B_i)log_2P(B_i) H=−i=1∑nP(Bi)log2P(Bi)
由此可以形象地把全概率公式看成为“由原因推结果”
每个原因对结果的发生有一定的“作用”,即结果发生的可能性与各种原因的“作用”大小有关。全概率公式表达了它们之间的关系。
(5)
贝叶斯网络
贝叶斯网络由网络结构和条件概率表组成
Ø 网络结构是一个有向无环图
Ø 每个结点代表一个事件或者随机变量
Ø 结点的取值是完备互斥的
• 对已有信息要求低, 可以在信息不完全情况下推理
Ø 采用条件独立性假设
• 具有良好的逻辑性和可理解性
Ø 贝叶斯网络是白盒,神经元模型是黑盒
• 可以与专家知识深度融合,避免过学习
Ø 突出主要矛盾
三个议题
• 贝叶斯网络预测
Ø 贝叶斯网络的预测是指从起因推测一个结果的推理,也称为由顶向下的推理
Ø 原因推导出结果,求出由原因导致的结果发生的概率
• 贝叶斯网络诊断
Ø 贝叶斯网络的诊断是指从结果推测一个起因的推理,也称为由底至上的推理。
Ø 已知发生了某些结果,根据贝叶斯网络推理计算造成该结果发生的原因和发生的概率
• 贝叶斯网络学习
Ø 贝叶斯网络学习是指由先验的贝叶斯网络得到后验的贝叶斯网络的过程
Ø 贝叶斯网络学习的实质是用现有数据对先验知识的修正
Ø 贝叶斯网络可以持续迭代修正
Ø 上次学习得到的后验贝叶斯网络变成下一次学习的先验贝叶斯网络
Ø 结构学习:确定最合适的贝叶斯网络模型结构
Ø 参数学习:在给定结构下,确定贝叶斯网络模型的参数,即每个结点上的条件概率分布表(CPT表)。

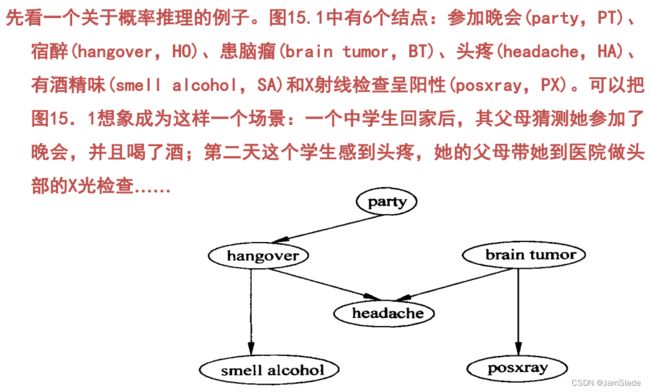
前例回顾
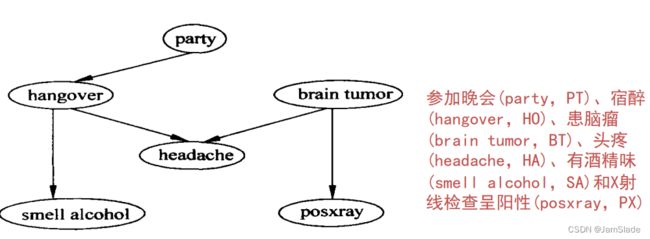
图15.1中的Party和Brain Tumor两个结点是原因结点,没有连线以它们作为终点。首先给出这两个结点的无条件概率,如表15.2所示。
表15.2中的第二列是关于Party(参加晚会)的概率:参加晚会的概率是0.2,不参加晚会的概率是0.8。第三列是关于患脑瘤的概率:患脑瘤的概率是0.001,不患脑
瘤的概率是0.999。
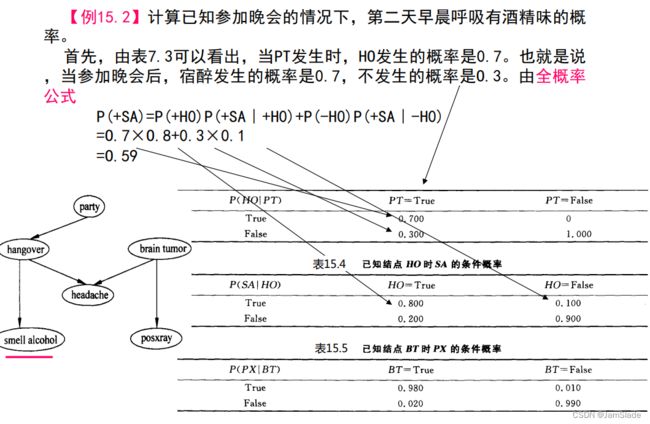
下面还将给出几组条件概率,分别是PT已知的情况下HO的条件概率,如表15.3所示;HO已知的情况下SA的条件概率,如表15.4所示;BT已知的情况下PX的概率,如表15.5所示。

上面三个表的结构相似,给出的都是条件概率。表15.3中第2列的意思是:当参加晚会后,宿醉的概率是0.7;不宿醉的概率是0.3。第3列的意思是:当不参加晚会后,不会发生宿醉的情况。
对表15.4和表15.5的解释类似。
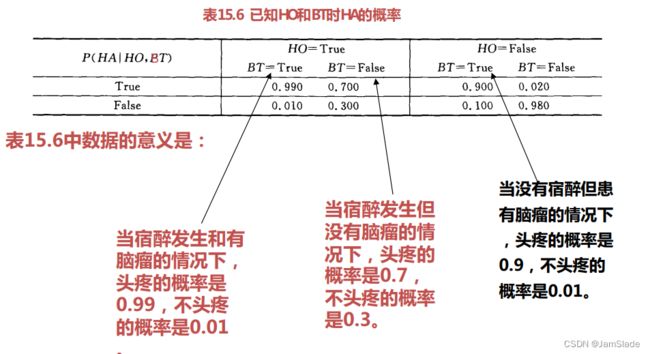
最后给出的是一个联合条件概率:已知HO和BT时HA的概率,如表15.6所示
【计算15.1】
【计算15.2】
【计算15.3】
【计算15.4】
【计算15.5】
【计算15.6】
【计算15.7】
如何构建?
- 节点
- 边
- CPT表