第3章 第1节-基于采样的路径规划-PRM&RRT及其优化
基于采样的路径规划(Sampling Based-Planners)
与基于search方法所不同的是,基于采样的路径规划不需要遍历空间所有点,而是通过在空间中随机撒点,通过线段连点构成路图/树(没有障碍的),来抽象的表达这个空间。 这个更高效,更适用于复杂环境、三维/高维空间
1. complete Planner完备规划器:在一定时间内,总可以找到一条路径从出发点到终点,A*就是
2. Probabilistic Complete Planner概率规划器:如果一个解存在(路径规划=找函数的解,如高斯法),使用随机采样的方法,改规划器最终能找到这个解
3. Resolution Complete Planner:和上面一样,但是基于一个确定的采样(如在一个fixed grid中采样
课程安排
1.概率路图
2.快速搜索随机树RRT
3.优化算法
4.Advanced 算法
5.实际应用
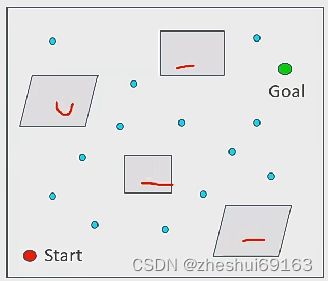
Probabilistic Road Map 概率路图(PRM)
PRM:是一种图结构
他把规划分为两个阶段:
1.学习Learning phase:学习地图结构:在环境中撒点,连点,从而做出一个图的结构,这是图的简化版,找路径直接在这个上找就会简单很多
1)采样
| (1)随机采点 | (2)障碍物中的点扔掉 |
|---|---|
|
2.连接相邻的点,得到无碰撞的有效分割
要求:
| (1)起点、终点要被连接到里面,点与点之间的连接要符合距离要求:太远的点不能连(如图不能连1-3,1-4等,避免路径太多,查询效率低)所以红色的线要删掉 | (2)有障碍物的点不要,所以删除绿色的线 |
|---|---|
2.查询 Query phase
直接用Dijkstra或者A*找到一条路径
直接A*等就很复杂,要很多网格计算
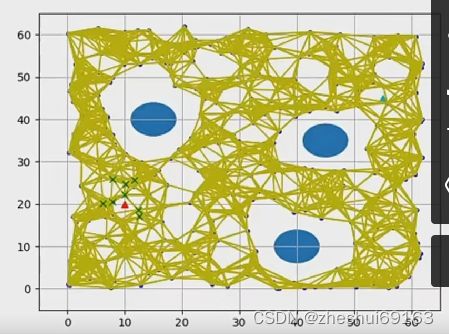
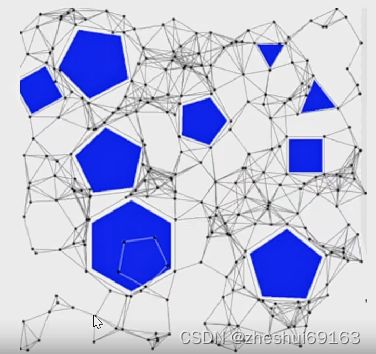
eg
| 1学习过程 | 2查询过程 |
|---|---|
 |
 |
 |
 |
优点Pros:概率完备的:若存在解,那么在空间中随机踩点,肯定可以找到解;相对于Dijkstra和A*不需要在整个环境中搜索,只要给出图(简化的环境)就可以找出,效率更高
问题Cons:要解决两点之间的约束,因为两个直线之间是不可导的,不适合机器人行走,要构造一条曲线满足机器人行走; 算法过于冗长,一开始就单纯的简化环境,没有考虑起始点与终点,相对不够有效率
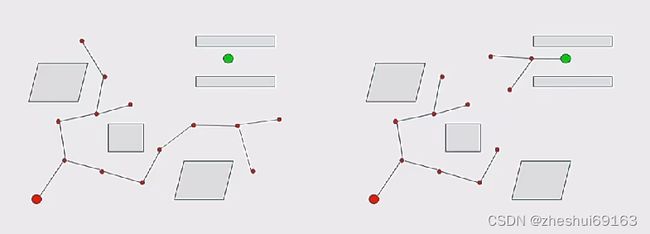
3.PRM改进-Lazy collision-checking
效率影响因素:检查点是否在障碍物内很耗时
Lazy collision-checking:直接不考虑点在不在障碍物内,直接不去点。这样生成的路径可能是经过障碍物的,那么再把这个不可行的点及其相关的路径删了,再重新构图,…,以此类推,直到找到可行路径

 |
| |
|
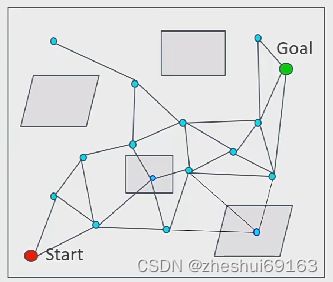
快速搜索随机树(Rapidly-exploring Random Tree)
相对于PRM更有针对性,能快速规划,在复杂/高维环境下搜索效率更高
在起点x init附近采样一些点构成树,相对于PRM是一种增量式的路径(首先采点,找树里面最近的点做一些连接,并且要障碍物检测,然后把新的点添加到树中,这个过程不断迭代,从而把树构建出来。直到把目标点也添加到树中,则可以找到从起始点到终点的路径
相对于之前的PRM,这个Tree方法不需要区分learning phase和query phase,他的目标就是构建一条路径,只要目标点被加入则反方向查询直接找到路径,而且不需要A*等算法。
伪代码:
输入:地图、初始点、终点
输出:起点到终点的路径
for i=1 to n do
第一次循环:(比较简单)
得到蓝色采样点,得到蓝色-红色路径,让红色往这条线上走 D e l t a Delta Delta距离,得到小的红色点,若这条段线段上没有障碍物,则原红色点+现在的线段=更新后的树

第二次循环
(1) x_rand<-Sample
Sample得到随机点x_rand
(2)x_near<-Near(x_rand,\Tau)
再刚刚生成的树上找一点距离x_rand最近的点x_near
(3)x_new<-Steer(x_rand,x_near,StepSize)
(4)E_i<-Edge(x_new,x_near)
(5) if CollisionFree(M,E_i) then \Tau.addNode(x_new) \Tau.addEdge(E_i)
Steer就是x_near到x_rand的连线上移动一定的距离StepSize,得到新的点x_new,和边Ei,如果这个edge Ei和Point x_new是collision-free的,那么这个点和边就加到树里面去,完成一次更新
后面的循环:若出现collision,则因为(5)中的判断条件,则边和点不会加到树中
最后
(6) if x_new=x_goal then Success(其实这力不应该直接说最后把绿色的点加入树就成功了,而是把绿色周围的点加到树中就成功了,因为绿色的点不一定会被随机采样到。如果绿色周围的点被选中,则也说明路径规划完成,只是有一定的偏移量
所以从终点倒着找父节点,最终找到起始节点,则路径就出来了
缺点:区域特殊,如下。落在狭窄区域的概率比较小,导致可能一直在一侧扩散
PPT的优势与缺点
优势Pros:相对于PRM,更有针对性的去找起点到终点的路径,速度较快
缺点Cons:不是最优路径(不是最短,也不是完全符合运动学约束)
改进:toward improving efficiency
1.Kd-tree
当重新选取一个rand点时,需要找打离其最近的点–笨方法是一一对比;Kd-tree工具:对所以点取横坐标的中位数,4,然后根据4划分成左右两支,再左右两侧分别纵坐标,…这个方法可以快速找到离你最近的点
2.Bidirectional RRT/RRT Connect
通过一次采样,在起点、终点处分别构建树,直到x_rand同时连接两棵树算法截止
有利于解决狭窄区域的概率比较小,导致可能一直在一侧扩散的问题,因为在终点也生成树了!
Bidirectional RRT 相对于单纯的RRT效率是高的,对于特例:终点在narrow path的问题也很有帮助,但对于narrow path问题他不是解决的唯一方式,更多的人倾向于通过改进采样的方式来解决narrow path问题:通过一些采样函数使得在狭窄区域落的点采样多一点(自行百度了解)