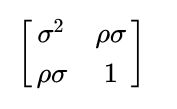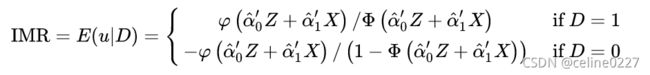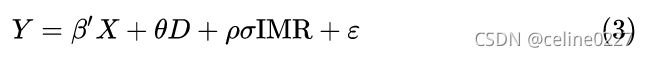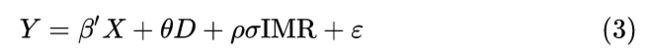Heckman 两阶段法及与工具变量法的区别

一、适用范围

Heckman两阶段模型适用于解决由样本选择偏差（sample selection bias）造成的内生性问题。

在经济学领域，样本选择偏差的典型例子是研究女性的受教育情况对女性工资的影响。按照这个思路，一般会去问卷收集或在哪个网站下载部分女性的受教育情况，工资，及其他特征数据，例如年龄，毕业院校等级等个人特征，然后做回归。不过这样做有一个问题，就是登记的女性，都是在工作的，但是许多受教育程度较高的女性不工作，选择做家庭主妇，这部分样本就没有算在内，样本失去随机性。这就导致模型只是用到了在工作的女性，这样得出的结论是有偏差的。

在管理学领域，一个典型的问题是企业的某个特征，或者董事/CEO的某个特征，对企业R&D投入的影响。也是同样的问题，企业的R&D投入是企业自愿披露的内容，有的企业不披露，这时你做回归时就不能包括这部分样本，也会造成样本选择偏差，结果有偏。

二、分析步骤

经典的赫克曼二阶段法，具体步骤如下：

第一步，研究者根据管理学理论设计出一个计算企业披露R&D投入概率的模型，而该模型的统计估计结果可以用来预测每个个体的概率

第二步，研究者将这些被预测个体概率合并为一个额外的解释变量，与其他控制变量等变量一起来矫正自选择问题。这个比率叫逆米尔斯比率，inverse Mills ration， imr，也就是说，在第一步计算出imr，在第二步把imr当作一个控制变量。

三、主要原理

选择模型有两种主要应用，一是 处理效应 (treatment effect model)，即回归模型中包含一个内生的指示变量 (D)。例如，管理层是否发布盈余预测 (D=1 或 0) 对资本成本影响。二是 样本选择 (sample selection model)，即回归样本为一个子样本。例如，在管理层发布盈余预测子样本中 (D=1)，对管理层盈余预测精确度的影响因素进行分析。在上述模型中，内生的 D 都会导致有偏估计。

处理效应模型 (treatment effect model) 如下：

其中， 包含截距项和一组影响  的外生解释变量。指示性变量  可以通过以下二元选择模型进行回归得到： 

通常，式 (1) 和式 (2) 的随机误差项  和  服从二元正态分布，其均值为 0，协方差矩阵为： 

 

如果随机误差项  和  相关 ()，则 ，使得式 (1) 中的 OLS 估计量  有偏。Heckman 方法就是通过式 (2) 构造 逆米尔斯比率 (IMR) 控制这个偏差。IMR 计算如下： 

 其中， 和  分别为标准正态分布的密度函数和累积分布函数。然后，将计算得到 IMR 加入式 (1) 进行回归：

此时，式 (3) 中随机误差项  与 D 不相关， 为无偏估计量。并且，可以通过 IMR 显著性和系数判断选择偏差是否存在以及方向。当然，式 (2) 和 式 (3) 可以用传统两步法或最大似然估计法。

上述为处理效应模型 (treatment effect model)，除式 (3) 是以子样本回归外，样本选择模型与处理效应模型 (sample selection model)类似。例如，对管理层预测精确度 (Y) 分析中，回归样本为发布盈余预测的公司 (D=1)。此时，式 (3) 为 

 其中，IMR1 计算公式如下：

 

IMR可以识别选择性偏差的主要原因：

选择模型式 (3) 与 OLS 模型式 (1) 的区别在于前者加入了逆米尔斯比率 ()。IMR 可以识别选择性偏差主要是以下原因：

• IMR 是  和  变量的非线性函数
• 变量从式 (3) 中已经排除

其中，Z 变量被假定为不会对  变量产生直接的影响，只能通过 IMR 产生间接影响，因此也被称为排他性约束 (exclusion restrictions)。

排他性约束变量，也就是 Z 变量，在控制选择模型内生性问题过程中具有非常重要的作用:

1.  变量必须是外生的，否则选择模型第一阶段回归 (式 2) 系数以及 IMR 会产生偏误；

2.  变量对 D 具有较强的解释能力，使得 IMR 能够更好的检测和控制选择偏差；

3. 式 (3) 中必须有效排除  变量的影响，即  变量只能通过 IMR 对  产生间接影响，否则  IMR 与随机误差项相关，使得  IMR 系数估计有偏，不能有效控制 D 变量的内生性。

找到一个好的  变量是困难的。在没有排他性约束情况下，即没有  变量，仍可以通过 IMR 的非线性去识别偏差。但可能面临以下两个问题：

• 由于只能通过 IMR 的非线性识别偏差，非线性模型被错误设定为线性模型会被 IMR 吸收。
• 在式 (3) 中，IMR  与  和 D 相关，这种相关性在没有排他性约束变量 () 情况下更加严重。

进一步，高的共线性会产生以下两个问题：

• 高共线性会使得系数的标准差变大，降低了系数的显著性。IMR  系数可能会变得不显著，进而得出错误结论。
• 在模型被正确设定下，即使存在高的共线性问题，系数也可以被无偏的估计。但是，事实上，选择模型被错误设定概率是很高的。若模型被错误设定，共线性会吸收这种偏差，导致系数估计有偏。

四、实例分析

以企业R&D投入问题为例，假设全样本是1000家公司，其中800家公司披露了其R&D投入。

第一阶段的模型，是一个包括全样本（1000家）的Probit模型，用来估计一家公司是否会披露其R&D投入的概率。这里的因变量是二元的，表示是否披露R&D投入；自变量是一些会影响是否披露R&D的外生变量，比如其他收入营业收入，杠杆率，公司规模，所属行业等等。然后根据这个Probit模型，为每一个样本计算出imr，IMR作用是为每一个样本计算出一个用于修正样本选择偏差的值。

第二阶段，在原来的回归方程，也就是原来只有800家公司的样本的方程假如imr作为控制变量，其他都不变，然后估计出回归参数。这时不管imr显著不显著都不重要，imr显著说明样本选择偏差的确影响了你最初模型的估计，这正表明了使用Heckman两步法纠正样本选择偏差的必要性。imr不显著说明原模型不存在严重的样本选择偏差，这时Heckman第二步得到的结果应该与原模型得到的结果差不多。(关于imr的显著性是否说明样本选择偏差存在目前还有争议，不过imr不是关注的变量)。第二步关注的对象是核心解释变量是否显著。只要核心解释变量显著，就说明结果稳健。

五、Stata实现

在stata上的实现，还是刚才的例子。假设问题是研究董事会的连锁懂事比例对企业R&D投入的影响，各变量如下：

因变量：企业R&D投入额度（rd）

自变量：董事会连锁懂事比例 （interlockratio）

控制变量：公司规模（firmsize），杠杆率（leverage）， 公司成长性（growth），公司年龄（age），行业R&D投入（industryrd），行业集中度（cr4），行业净资产收益率（industryroa）等。

其中前三个控制变量还会影响企业R&D投入的概率。

总样本数1000家，其中800家披露了R&D投入，不考虑其他变量的缺失值。

Heckman两步法
第一步，命名一个新的因变量，企业是否披露R&D投入，ifrd
xi: probit ifrd firmsize leverage growth i.year i.ind  r//Heckman两阶段的第一阶段回归，这里的r可加可不加，看需不需要控制异方差问题。
estimate store First
predict y_hat, xb
gen pdf = normalden(y_hat)  
gen cdf = normal(y_hat)  
gen imr = pdf/cdf//生成imr
 第二步回归，把imr当作控制变量加入原模型，用原来的数据。
reg rd interlockratio leverage growth industryrd cr4 industryroa imr i.year i.ind , r if ifrd==1

六、回归变量选择

需要注意的是，在第一步，确定哪些变量会影响企业披露其R&D数据时，这些变量不一定是原模型的因变量，可以是可以不是，是不是要说明理由。

要真正解决样本选择问题，总样本模型中的解释因子群应该是选择模型（披露了R&D投入）的解释因子群的完全子集。而且，在选择模型中，至少要有一个解释变量不出现在主体模型之中。文章通常会选取与因变量不相关的变量加入进行估计。

eg. 在陈云松（2012）：农民工收入与村庄网络，《社会》发表的文章中，家庭劳动力数量被视为和农民工在城市的工资收入无关的因素而纳入打工决策的Logit模型

七、 与工具变量区别

Heckman二阶段法只能解决样本选择问题，对于一般性的因遗漏变量引发的估计偏误和联立性问题（双向因果）却无能为力。

为解决这个问题，在陈云松（2012）：农民工收入与村庄网络，《社会》发表的文章中，Heckman二阶段模型的基础上进一步采用工具变量方法。这个工具变量必须是一个和农民工在城市的工资收入没有任何直接关系，但却又可以有力地影响村庄外出打工者数量的外生变量。利用工具变量所引发的自变量的差异，可以获得对因变量的无偏估计。