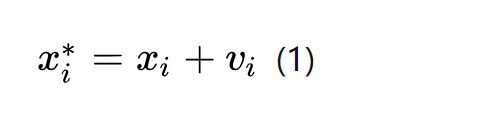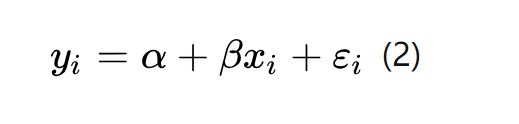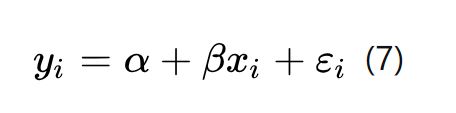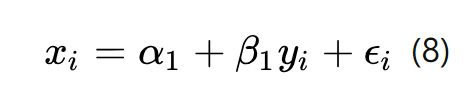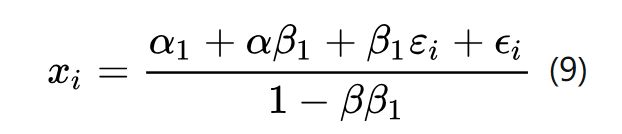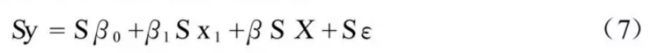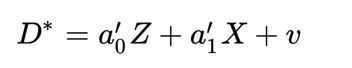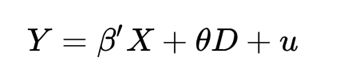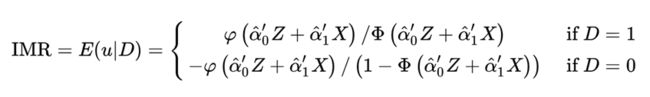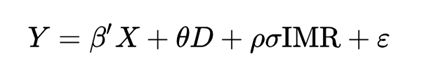Heckman模型学习笔记

Heckman模型学习笔记

1、内生性

1.1 线性回归估计原理

我们做线性回归的时候，需要做一些假设，包括：

1）线性性

回归模型对参数而言是线性的，回归子Y和回归元X可以是非线性的。（估计参数本身就是一个随机变量，在进行估计时，X看为固定值，那么对应的条件均值Y与关系应该为线性的。参考logit y=bx)

2）重复抽样种，x视为固定

实际上，我们估计的是E(Y|X=X0)条件均值。

3）误差项（εε）之间独立同分布~N(0,），同y

y=bx+ε,所以y与ε同态同方差。因此，ε的正态性是保证我们估计出来的y的条件均值能代表其平均水平的重要条件。异方差则会导致最小二乘法估计的参数检验失效。而且，由于，我们是通过多个不同的x对应Y的数据来估计其条件均值的，没有同一个x对应的y的重复数据，因此我们是无法得到y的方差的，所以，我们需要假设其同方差，这样才能够利用多个(x,y）来估计其方差。然后，才能对参数进行各种假设检验。

 4）观测次数n大于待估计的参数个数

会解方程的都懂

5）无完全多重共线性

1.2 何为内生性

我们都知道，在一个回归方程里，等号左边是因变量，右边是自变量。在联立方程模型里，我们有几十乃至几百个方程，所以每个变量都可能同时出现在方程 A 的左手边和方程 B 的右手边。也就是说，这些变量的值既被其他变量决定，又能够影响另外一些变量。它们在整个模型中起了中间环节的作用，因此被称为 “内生变量”（只出现在左手边的变量显然也是内生的）。如果我们假设每个变量都是内生的，那模型中的参数就会太多，以至于根本无法估计（不可识别）。所以，研究者必须根据理论或者现实观察，对模型加以简化，假设某些变量只出现在各个方程的右手边，这些纯粹的 “输入” 就被称为 “外生变量”。正是外生变量的存在，使得我们可以 “识别（identify）” 模型中的参数。这是内生性这个名词的由来，从今天的角度来看，联立方程模型当然充满了各种问题：为什么方程都是线性的？这么多关系式是从何推导而来？因此在经济学和政治学中，这套方法已经不再时兴。但是，这整个体系时至今日，还在很大程度上左右着社会科学家们对实证研究的评判。而广义上的内生性则是指模型中的一个或多个解释变量与误差项存在相关关系。 

而内生性会导致什么呢？它会破坏掉参数估计的一致性（当样本量很大时，用样本估计出的参数会无限趋近于总体的真实参数。当我们用样本估计出的参数没有了一致性，那它也就没什么参考价值了。）（待理解原因）

1.3 内生性的种类

1）测量误差（measurement error）

测量误差指的是模型使用的解释变量的数值和真实数据有误差。假如解释变量 出现了测量误差，我们测得的数据为二者之间有了一个误差 :

假设真实x与y之间的关系为：

那么把替代进去就是：

如果，我们算与y的回归关系，则会得到（4）的回归式，而其中随机误差项为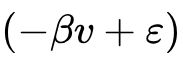而解释变量跟其协方差为：
显然不等于0.

3）互为因果（simultaneity）

被解释变量能够反过来影响解释变量的情况被称为互为因果，有时也被称为反向因果（reverse causality）。设想我们设计了这样的模型：

但同时，y又反过来影响x:

联立78可得：

4）选择偏误

包括样本选择偏误和自选择偏误，自选择偏误指因变量在某种程度上是被个人选择决定的，样本选择偏误则是指，某些因变量数值不可及，而得到的非随机样本，导致失去样本的普遍性。

例如，若我们想研究妇女年龄与工资收入，虽然我们可以观测到有工作的妇女的实际工资收入，但是不知道没有工作的妇女的“保留工资”（即愿意工作的最低工资，如果低于最低工资则不选择去工作，而我们是无法得到不去工作的那部分女性的工资水平的）。于是我们收集数据时就会缺失没有选择工作的妇女样本。

此时，我们以为我们估计了工资与年龄的关系：

实际上，我们估计的是选择工作的人：

而在7中，如果存在x1即影响是否工作，又影响工资水平，则会导致（7）式中存在内生性。

 

2、heckman模型

1、产生背景

1974年，Heckman首次提出样本选择模型及其似然估计，应用于市场工资与妇女劳动力供给关系研究。1979年，Heckman对模型进行完善，提出两步法，得到学术界认可。此后二十年，该模型在国外经济学和社会科学领域得到了广泛应用和认可。2000年，Heckman因解决样本选择偏倚被授予诺贝尔经济学奖。此后，Heckman模型引入国内并逐渐引起重视，应用于各个领域用于解决内生性问题。

2、模型介绍

Heckman样本选择模型主要包含两部分内容，一是选择方程模型，用于分析样本的选择行为（例如，妇女是否选择去工作D=0,1）；二是结果方程模型，用于消除样本选择偏倚后对实际结果进行预测，其中包含了内生的指示变量D。

heckman两步法：

通俗来讲，由于某些原因，部分样本的结果变量未知，而我们只能用部分已知结果的样本进行模型拟合，因此，存在偏差，即样本是否选择，这一变量。当影响是否选择这一变量的自变量与研究结果y的自变量无重合部分时，可以说是否选择与结果y无关，这时适用已有结果的样本进行拟合模型是无偏的，但若二者中有重合变量，则会导致模型有偏，此时使用选择方程模型拟合出逆米尔斯率纳入结果方程模型中，可以很好的解决这一问题。

3、Heckman模型的使用方式

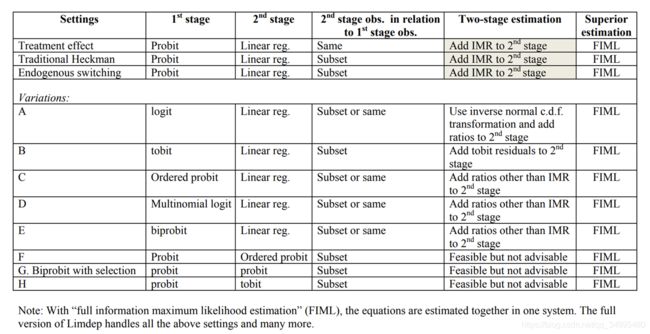
上文介绍了heckman模型中经典的二步法，但不是所有的情景都可以使用两步法来解决的。两步法的本质是选择方程模型使用一个probit二分类模型，得出一个逆米尔斯率纳入第二个结果方程模型中，进行OLS回归。所以，在使用两步法的时候，第一阶段应该是一个二分类的选择行为，二第二阶段最好是一个因变量为连续性变量的回归模型（因变量若为二分类变量的话可以使用但不被建议，原因同线性概率模型的局限性）。

而在我们平时使用模型时，结果方程模型的因变量很多情况下都不是连续性变量（此时两步法失效，应使用全阶段似然估计），或者第一阶段选择方程模型中选择行为有大于两种，这时可能需要使用logistics多分类模型，这时将逆米尔斯率添加到第二阶段方程中也不合适，因为probit和logistics模型的累积函数不同，所以需要对逆米尔斯率进行转化。具体情况分类如下表格：