机器视觉笔记：RANSAC算法以及思想
目录
- 1.问题背景
-
- 1.1误差和粗差
- 1.2举例
- 2.RANSAC算法过程
-
- 2.1RANSAC算法思路
- 2.2RANSAC算法过程
- 3.算法结果
- 结语
1.问题背景
- 在对观测数据处理的过程中可以发现，由于噪声的存在，实际的观测值会与其真实值存在一定的差值。RANSAC算法的目的就是尽可能地减少这些差值对系统的影响。
1.1误差和粗差
- 影响我们的观测结果的差值可以分为误差和粗差两个部分（可能不书里面的名称不太一样）。其中误差来源于对目标的多次观测，从而不可避免地产生了一些微小的差距，而粗差则来源于错误的观测。
- 举个例子：假如你用尺子去测量铅笔的长度（假设尺子有足够的精度，而铅笔正好是10cm的长度），测了10次以后发现几乎每次测量的结果都是准确的10cm，总有0点几毫米的差距，这就是误差。而如果你本来计划去测量铅笔，却测量了中性笔的长度，最后的结果自然就是错误的了，这个就是粗差。
- 从这个例子我们可以看出来误差和粗差的存在对观测结果会产生一定的影响，误差对观测结果的影响较小，而粗差对观测结果的影响较大，甚至直接产生一个错误的测量。
1.2举例
- **再举一个例子：**在计算机视觉的相关领域中（比如SLAM），需要对图像的特征点进行提取的匹配，从而完成对相机位姿的估计。针孔相机成像的过程是三维空间点通过相机的内参、外参矩阵映射到相机产生的图像的像素中，相机模型不做赘述，公式如下：
Z P u v = Z [ u v 1 ] = K ( R P w + t ) = K T P w ZPuv=Z\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=K(RPw+t)=KTPw ZPuv=Z⎣⎡uv1⎦⎤=K(RPw+t)=KTPw - 由于世界坐标是连续的，而无论分辨率多高，相机成像始终是在离散平面的某像素点处成像，而且在计算图像特征的时候，也不能十分准确地定位特征点，再加上相机本身标定的误差，都会导致成像的时候有一定误差。这就是相机系统中误差的来源，在实际使用的过程中，一般会将这种误差拟合为一个高斯分布的模型，后续通过一系列优化方法进行优化。
而在特征点匹配的过程中，会有很多误匹配，如下图中虽然找到了很多特征点，但是许多特征点匹配地并不正确（比如有一条黄色的线，将电脑屏幕角与键盘角匹配到了一起）。
这些误匹配会给后续的相机位姿估计带来巨大的影响，在统计学中属于离群点，这些就是粗差点。过多的误匹配将会导致相机位姿估计越来越离谱。因此就需要通过某些算法来实现对这种误匹配的粗差点进行剔除，RANSAC算法就是一种剔除离群点的很好的一种方法。
2.RANSAC算法过程
2.1RANSAC算法思路
RANSAC算法的思路就是从所有观测中随机找到几个尽可能少的点去拟合模型，拟合后依次计算模型和所有观测数据的残差，当残差小于给定的阈值时，就将其判断为内点，大于给定的阈值时，就判断为外点，并统计内点的数量，然后再次随机选取几个点拟合模型迭代。如果本次拟合内点数量大于先前的模型，就将旧模型迭代为新的模型。
2.2RANSAC算法过程
以二元的最小二乘回归问题为例，如下图：
- 红色点为内群点（包含高斯分布的误差），而黑色点为不符合回归模型的离群点，红色直线为通过群内点拟合出的回归模型（也就是理想中的拟合模型），黑色直线为所有点的拟合模型，可见，黑色与红色之间存在较大的差距，结果不可信：
算法过程具体如下：
-
在所有点集中随机选取2个点，拟合模型，得到最初的模型; - 统计在容限误差内的点的数量; - 再次在所有点集中随机选取两个点，再次拟合模型; -统计在容限误差内的点的数量，如果这次数量增加，则将旧模型替换为新的模型;如果小于之前的模型，则直接进入下一次迭代; -
若到达最大迭代次数，则终止算法。
2.3参数确定
RANSAC算法中主要有两个参数，一个是最大迭代次数，一个是容限误差。
最大迭代次数可以通过如下公式导出：
K = l o g ( 1 − p ) ) l o g ( 1 − w n ) ) K=\frac{log(1-p))}{log(1-w^{n}))} K=log(1−wn))log(1−p)) -
式中：
K——最大迭代次数 p——算法跑k次的成功率 w——随机抽取一个点是内群点的概率 n——每次拟合模型选择的点的个数 -
虽然这个公式中有未知数w，但是可以发现，当n越小的时候，算法的成功率越大。因此需要用尽可能少的观测数据拟合。而容限误差也是一个先验的参数，可以计算（还没研究明白，以后补上）
-
增加了 检查列表 功能。
3.算法结果
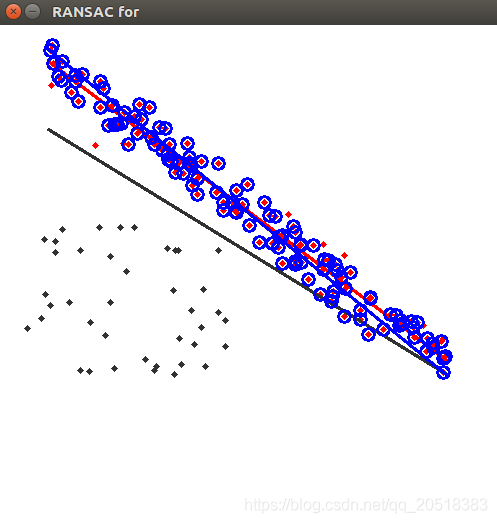
算法的迭代是随机的过程，所以每次迭代的结果不固定，但是最终都会收敛于数据的真实分布。蓝色线条为RANSAC算法拟合的模型，蓝色圈为算法判断的内群点：
- 算法第1次迭代的结果：
- 算法第4次迭代的结果：
算法第254次迭代的结果：
- 算法第最终迭代的结果：
- 最终可以看到，红蓝线条重合，算法收敛于Ground_Truth，成功排除了离群点对于模型拟合的影响。
4.代码：
- 其实这类代码用python比较明晰，不过为了锻炼C++编程能力，虽然C++比较繁琐，还是用C++来写啦：
#include 结语
- 时间仓促，对于RANSAC算法的理解还有不正确的地方，欢迎指正。代码注释也没来得及完善，留待以后。自我感觉RANSAC更像是一种思想，而不是一个固定的算法。所以以后再遇到类似里群点剔除、滤波等问题时，RANSAC将会是一个很好的思路。
第一次写博客，写的不好，欢迎指正～