【矩阵论】线性空间与线性变换（6）
有关线性映射的[值域空间]和[核子空间]的讨论
一. 满射、单射与双射
- 定义回顾
在前一篇文章《【矩阵论】线性空间与线性变换（5）》中我们对线性映射的值域和核子空间进行了定义：
同样地，我们也对线性映射的类型进行了讨论：
2. 定理描述
首先：根据线性映射的满射和单射，其值域空间和核子空间分别会与集合U和零空间相等。
又因为：两个有限维度的线性空间相等，可以转换成证明两个空间的维度相等；
因此：要证明一个线性映射是满射或者是单射，只需要证明线性映射的值域空间维度与U维度一致+证明线性映射的核子空间维度为0.
- 定理证明
下面对上述定理中的第二条充要条件进行证明。
【必要性】：已知f为单射，要证明f的核子空间为零空间。
要证明一个空间为零空间，则需要证明对于任意一个向量η∈K(f)，都有η = θ。
按照核子空间的定义，应该有f(η) = θ；又因为f是一个线性映射，所以应该有f(θ) = θ；
那么按照单射的定义，只可能是η = θ。
#证毕
【充分性】：已知线性映射f的核子空间是零空间，要证明映射f是一个单射。
假设存在两个向量x,y，其映射之后的像相等，也就是【f(x) = f(y)】，变形后也就是【f(x)-f(y) = θ】
根据线性映射关于线性运算封闭的定义，则有【f(x-y) = θ】，那么左式是符合核子空间的定义，则【(x-y)∈K(f)】
即：(x-y) = θ，从而推出x = y。
- 【值域空间】基与维数的求解
按照前面我们讨论以及证明的定理来看，在求解单射、满射以及双射的相关问题时，我们需要对映射f的值域空间R(f)和映射f的核子空间K(f)进行求解。
（1）定理描述
（2）定理理解
我们要求解R(f)的基，也就是求解R(f)的极大线性无关组。根据定义，直到R(f)是由f(α1)，f(α2)，f(α3)，…，f(αs)这组向量张成的线性空间，那么问题就可以转换成求解f(α1)，f(α2)，f(α3)，…，f(αs)的极大线性无关组。
根据线性映射的矩阵描述，我们可以得到如下等式
f(α1)，f(α2)，f(α3)，…，f(αs) = （β1，β2，…，βs）A
其中矩阵A写成列分块矩阵后，第i列就是f(αi)这个向量在（β1，β2，…，βs）这组基下的坐标。
根据我们讨论过的【向量与坐标的等价性】，问题再一次被转换成求解矩阵A的极大线性无关组，使用初等行变换即可。
矩阵A具有的一些空间性质（维度，极大无关组，线性相关性等）都可以自然地延伸到R(f)这个待求空间上。
- 【核子空间】基与维数的计算
（1）定理描述
（2）定理理解
因为核子空间是基于一个约束式子f(δ) = θ进行定义的，其自身的理解并不是很直观。所以我们要先把核子空间的一般形式求解出来，找到该空间的直观表示方式后，再求解该空间的基与维数。
按照上图中给出的线性映射的矩阵表示，在V中的任意一个向量η，其坐标为X，经过映射后，其坐标为AX。
如果，η这个向量同时也在f的核子空间中，那么就有f(η) = AX = θ，也就是映射后的向量在基β1，β2，…βn的坐标表示是θ向量。
那么，对核子空间的求解，转化成对于齐次方程组AX = θ进行求解；
求解核子空间的极大无关组，也转化成求解方程组的基础解系。
（3）维数定理——核子空间和值域空间
在前一篇文章中我们是通过例题计算验证了这一结论，这里我们通过数理逻辑对这一结论进行了证明。
【推论】对于一个可逆的变换（双射），证明单射和满射是互为等价的
证明思路如下，以下步骤均为等价变换
若f是一个单射，根据性质，核子空间K(f)为零空间，则K(f)空间的维度即为0，代入维数定理中可以得到，值域空间R(f)的维度和集合V的维度相等，则有R(f) = V，按照定义，就说明f是满射。
【例】求解f的值域空间和核子空间 - 1
<求解值域空间>
对A进行初等行变换，可以从中求得值域空间的维数性质。
注意！！在求基的时候，要代回到没有进行初等行变换的矩阵。
因为按照线性变换f的矩阵表示，满足的是f(α1)，f(α2)，f(α3)，…，f(αs) = （α1，α2，…，αs）A，也就是A的第i列为f(αi)相应的坐标表示。
所以最后求解出来的基是ε1+ε3,2ε1-ε2+ε3；而不是ε1，ε2.
<求解核子空间>
对于齐次方程组AX = θ求解基础解系，同样是对A进行初等行变换，可以得到解空间的基础解系为[-2,1,1]T。
找到基础解系后，核子空间和值域空间略有不同，它是一个抽象的线性空间，而非从列向量中进行选择。
确定了基之后，就能把核子空间的基完整表达出来，同时也确定了空间的维度。
【例】求解f的值域空间和核子空间 - 2
由题需求，给出的某一个线性变换的值域空间R(f)与核子空间K(f)的基和维数。
根据前面的定义，只需要找到线性变换集合F2x2中的一组基，以及在这一组基下变换f的矩阵即可。
之后R(f)空间和K(f)空间就可以借助矩阵来进行求解。
<求解线性变换的矩阵A>
通常要求解线性变换对应的矩阵，按照线性变换矩阵表示的定义，打好框架即可。
选取的F2x2的基就是最自然的那一组E11，E12,E21,E22
代入到线性变换的定义式中，即可以求解出矩阵A。
<值域空间的求解>
对求解出来的矩阵A进行初等行变换，值域空间和矩阵A的列空间具有相同的性质。
同样要注意我们在第一个例题中讲过的，最后找基的时候，要借助原来的A矩阵的各个列向量来看。（不能使用经过行变换后的矩阵）
<核子空间的求解>
求解出了值域空间的维数之后，根据维数定理马上就能得到核子空间的维数为1.
同样需要对A进行初等行变换，转换成最简形矩阵，解得以矩阵A作为系数矩阵的齐次线性方程组AX = θ的基础解系。
在上图中，基础解系中含有的向量就是[-1,1,-1,1]T
要注意的是，求出来的基础解系并不是最终我们需要的核子空间的基，我们求出来的只是基在选定的E11,E12,E21，E22这组基的下的坐标。
因此最终我们需要的解是-E11+E12-E21+E22 = [[-1,1],[-1,1]]这个矩阵。
二. 不变子空间
【前言】
我们前面花了很多篇幅讨论了线性映射的矩阵表示，以及通过矩阵来进行相关性质的求解。
其核心就是，对于一个从V到V的映射f，我们在找到V的一组基α1，α2，α3，…，αs之后，可以把线性映射表示成基于这组基的一个矩阵A。
而我们引出“不变子空间”这个概念，就是希望我们可以尽可能地使矩阵A的表示简单一点。
- 不变子空间的定义
也就是对原来从V到V的一个映射，我们能在V中找到一个子集W，使得映射f在w上的部分，也是从w到w变换的，不会出现从w映射到(V-W)的部分。
- 讨论“不变子空间”的重要性
根据上图，若将线性变换的原始集合V分解成两个不变子空间的直和，那么根据我们在《【矩阵论】线性空间与线性变换（3）（4）》中所讨论的直和的定义与性质
不变子空间V1和不变子空间V2分别都可以找到一组基，而两个不变子空间的基的和就是最终的空间V的基。
此时，若我们想要对线性映射f进行矩阵表示，按照打好的框架就有
(f(a1)…f(ar),f(ar+1)…f(an)) = (a1 a2…ar,ar+1,…,an)A的形式
其中，f(a1)…f(ar)只在V1不变子空间中出现，可以只表示成a1 a2…ar的线性组合的形式；
同理，f(ar+1)…f(an)可以只表示成ar+1,…,an的线性组合的形式。
那么，线性变换的表示矩阵A就可以写作一个分块对角阵，其形式和运算得到很大简化。
【例】利用不变子空间的定义对线性映射进行相关求解
根据题意，要证明线性映射f在任意基下的矩阵均相似于[[I,O],[O,O]]；实际上就是要找到存在一组基，使得线性变换f在这组基下的矩阵表示就是[[I,O],[O,O]]。
因为在《【矩阵论】线性空间与线性变换（5）》这一节中的第四部分中，我们进行过证明，“不同基表示下的线性变换的矩阵都是相似的”。
那么问题就转换成如何找到满足条件的那一组基。因为给出的矩阵的形式是分块对角阵，因此想到利用前面讨论过的有关不变子控件的定义和定理，把线性映射的集合V展开成两个不变子空间的直和。
由上图，构造出V1和V2两个子空间，现需要证明V就是这两个子空间的直和。
在《【矩阵论】线性空间与线性变换（3）（4）》中我们讨论过有关直和的定义和性质，以下进行简短回顾，如果想详细了解，可见上文。
要证明V是V1和V2的直和，只需要证明两点即可。
其一：V1和V2的交集为零空间
也就是从V1∩V2中任取一个向量，要能推出该向量为零向量。
根据V1和V2的定义，η∈V1∩V2，则有η∈V1和η∈V2，那么即f(η) = η = θ，则η = θ。
其二：V = V1+V2
要证明两个集合相等，按照老套路，只需要证明两个集合相互包含即可。
显然可证V包含V1+V2，不再论述。因为V的定义能对V1和V2的定义同时满足。
以下只对V1+V2包含V进行证明，也就是任取一个元素η属于V，要证明该元素η也属于V1+V2
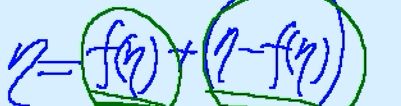
将任意一个元素η拆解成上述形式，可以证明f(η)是在V1空间内的，η-f(η)是在V2空间内的，故就证明了任意一个V中的元素都可以表示成V1中的元素和V2中的元素之和的形式。
通过上面的论述证明了V是V1和V2的直和，现在需要对这个线性变换f进行矩阵表示。
对于空间V1找到一组基ε1，ε2，…,εr
对于空间V2找到一组基εr+1,εr+2,…,εn
那么根据直和的性质，空间V的基就是ε1，ε2，…,εr,εr+1,εr+2,…,εn
按照上图的右边部分打好求解矩阵的框架，那么第一列就是要求解f(ε1)在基ε1，ε2，…,εr,εr+1,εr+2,…,εn下的坐标。
又因为f(ε1)是在V1子空间中，根据V1子空间的定义，知道f(ε1) = ε1，所以第一列的坐标可以写作是1,0,0,…0.
同理，就可以得到最后的表示矩阵形如[[I,O],[O,O]]
以上，需要对线性变换所对应的矩阵进行一个简单的表示，实质上对集合进行恰当的直和分解。