第五章 阻抗匹配与调谐 Smith圆图
这里写目录标题
- 5.1 Smith圆图
-
- 归一化电阻
- 归一化电抗
- 归一化阻抗rx
- 等驻波比圆
- 导纳gb
- 对比
- 5.2 分立元件匹配网络
-
- L形匹配网络
- 最佳功率传输
- 例题8.1 教材274页 PDF290页 ★
- 例题8.2 教材276页 PDF292页 ★
- 8.1.2 匹配禁区 教材280页 PDF296页
- 5.3 LC串并联谐振回路
-
- (1)串并联支路阻抗变换
- L型阻抗匹配网络计算分析
-
- 例题
- 8.1.3 T形匹配网络和π形匹配网络
-
- T形匹配网络 教材285页 PDF301页 例8.5
- π形匹配网络 教材286页 PDF302页 例8.6
- 5.4 微带线匹配网络
-
- 5.4.1 从分立元件到微带线
- 教材288页 PDF304页 例8.7
- 8.2.2
-
- 实部匹配
-
- 实部匹配方法一
- 实部匹配方法二
- 虚部匹配
- 短截线长度
- 例匹配网络的拓扑结构如图
- 单节短截线图解法
- 作业
5.1 Smith圆图
Γ = Γ r + j Γ i = ∣ Γ ∣ e j θ L = ∣ Γ ∣ ∠ θ L \Gamma = {\Gamma _r} + j{\Gamma _i} = \left| \Gamma \right|{e^{j{\theta _L}}} = \left| \Gamma \right|\angle {\theta _L} Γ=Γr+jΓi=∣Γ∣ejθL=∣Γ∣∠θL★
0 ≤ ∣ Γ ∣ ≤ 1 0 \le \left| \Gamma \right| \le 1 0≤∣Γ∣≤1
无耗传输线
Γ ( d ) = Γ 0 e − j 2 β d = Γ 0 e j 2 β z \Gamma \left( d \right) = {\Gamma _0}{e^{ - j2\beta d}} = {\Gamma _0}{e^{j2\beta z}} Γ(d)=Γ0e−j2βd=Γ0ej2βz
归一化电阻
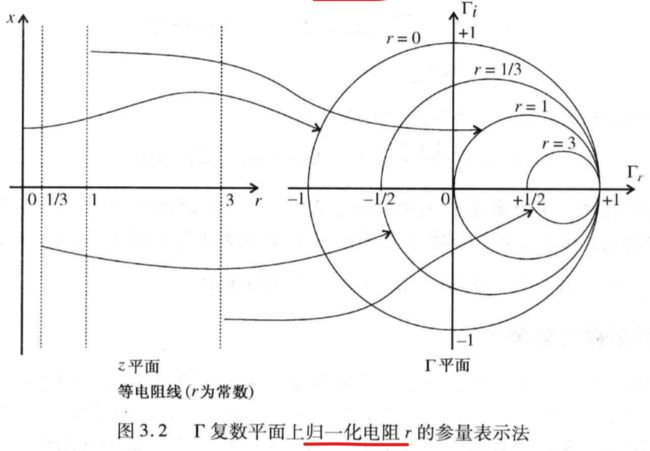
圆心 ( r 1 + r , 0 ) \left( {\frac{r}{{1 + r}},0} \right) (1+rr,0)
半径 ( 1 1 + r ) \left( {\frac{1}{{1 + r}}} \right) (1+r1)
半径越小,电阻r越大
单位圆内, − 1 < 1 1 + r < 1 -1<{\frac{1}{{1 + r}}}<1 −1<1+r1<1,电阻 0 ≤ r < ∞ 0≤r<∞ 0≤r<∞
归一化电抗
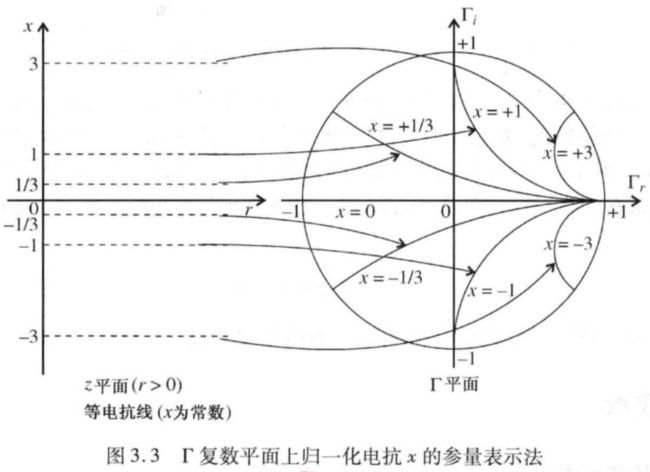
圆心 ( 1 , 1 x ) \left( {1,\frac{1}{x}} \right) (1,x1)
半径 ( 1 x ) \left( {\frac{1}{x}} \right) (x1)
半径越小,电抗x越大
归一化阻抗rx
等驻波比圆
S W R = 1 + ∣ Γ ∣ 1 − ∣ Γ ∣ ⇒ ∣ Γ ∣ = S W R − 1 S W R + 1 SWR = \frac{{1 + \left| \Gamma \right|}}{{1 - \left| \Gamma \right|}}{\rm{ }} \Rightarrow \left| \Gamma \right| = \frac{{SWR - 1}}{{SWR + 1}} SWR=1−∣Γ∣1+∣Γ∣⇒∣Γ∣=SWR+1SWR−1★
圆心原点,代表匹配点:
终端匹配 Z L = Z 0 ⇒ Γ 0 = 0 {Z_L} = {Z_0} \Rightarrow {\Gamma _0} = 0 ZL=Z0⇒Γ0=0
半径 ∣ Γ ∣ \left| \Gamma \right| ∣Γ∣
圆与实轴的交点处的对应归一化阻抗的r值=SWR值
导纳gb
y = 1 z = Z 0 Z = 1 / 1 Z Z 1 / 1 Z 0 Z 0 = Y Y 0 = y r + j y i = 1 − Γ 1 + Γ = 1 + e j π Γ 1 − e j π Γ y = \frac{1}{z} = \frac{{{Z_0}}}{Z} = \frac{{{1 \mathord{\left/ {\vphantom {1 Z}} \right.} Z}}}{{{1 \mathord{\left/ {\vphantom {1 {{Z_0}}}} \right.} {{Z_0}}}}} = \frac{Y}{{{Y_0}}} = {y_r} + j{y_i} = \frac{{1 - \Gamma }}{{1 + \Gamma }} = \frac{{1 + {e^{j\pi }}\Gamma }}{{1 - {e^{j\pi }}\Gamma }} y=z1=ZZ0=1/1Z0Z01/1ZZ=Y0Y=yr+jyi=1+Γ1−Γ=1−ejπΓ1+ejπΓ★
e j π = − 1 {e^{j\pi }} = - 1 ejπ=−1
可以看出,这相当于将 Γ \Gamma Γ旋转180度
将z对应的点旋转180度,再读出的z值就是导纳值
将坐标系旋转180度读出的值就是对应的导纳值
对比
| ★★★ | 阻抗圆图 | 导纳圆图 | |
|---|---|---|---|
| 圆心在上半平面1/x>0 | 电感性 | 电抗x>0 | 电纳b<0 |
| 圆心在下半平面1/x<0 | 电容性 | 电抗x<0 | 电纳b>0 |
| 最左边 | 短路点 | 阻抗 z = 0 z=0 z=0 | 导纳 y → ∞ y→∞ y→∞ |
| 最右边 | 开路点 | 阻抗 z → ∞ z→∞ z→∞ | 导纳 y = 0 y=0 y=0 |
5.2 分立元件匹配网络
内阻为ZS的电压源连接阻抗为ZL的负载,要使负载上要获得大的实功功率,需满足 Z S = Z L ∗ {Z_S} = Z_L^ * ZS=ZL∗
实际电路中,这种条件往往得不到满足
要得到最大的功率传输需要在电源和负载之间插入一个网络
插入网络不能消耗能量,因此只能是LC网络
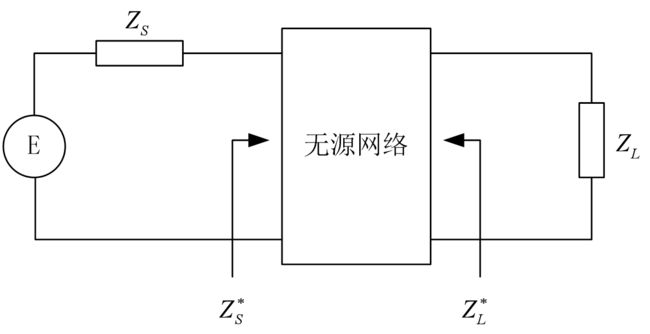
常用的匹配网络有L ( Γ ) \left( \Gamma \right) (Γ)形,T形和π形网络。
设计方法有解析法、Smith圆图法等
解析法计算结果准确,但不够直观
Smith圆图则较为直观,容易
实际上Smith圆图也以解析式为基础,利用计算机辅助设计,也可以方便、精确的做到阻抗匹配。
Smith圆图做阻抗匹配的基本思想是用特定的线段代表加入的匹配元件,当源阻抗点通过特定的线段与目标阻抗点连接时,就完成了阻抗匹配
假设有一个负载,阻抗为ZL ,在Smith圆图上表示为一个点。即归一化阻抗点
由于Smith圆图是阻抗图和导纳图合为一体的,因此同一个点可以表示为阻抗形式或导纳形式
z = Z L Z 0 = r + j x y = Y L Y 0 = g + j b {z = \frac{{{Z_L}}}{{{Z_0}}}{\rm{ = }}r + jx}\\ {y = \frac{{{Y_L}}}{{{Y_0}}} = g + jb} z=Z0ZL=r+jxy=Y0YL=g+jb
Y L = 1 Z L Y 0 = 1 Z 0 {{Y_L} = \frac{1}{{{Z_L}}}}\\ {{Y_0} = \frac{1}{{{Z_0}}}} YL=ZL1Y0=Z01
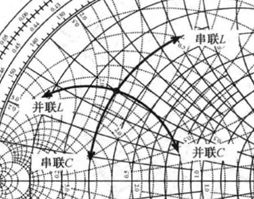
| ★★★ | 源阻抗 | |
|---|---|---|
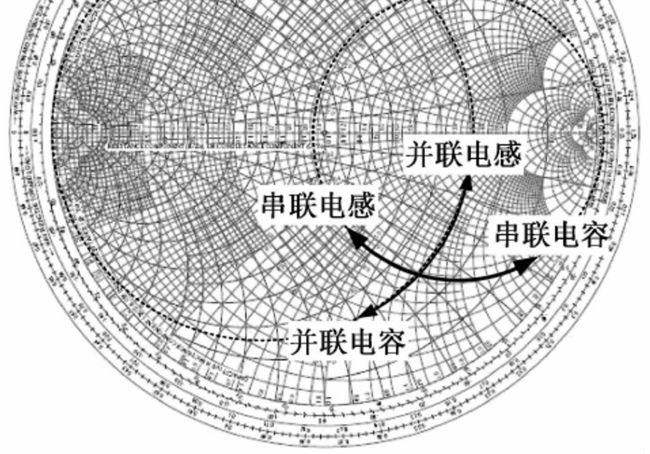
| 串联电感 | 沿着等电阻圆(单位圆内,圆心靠右的) | 向顺时针移动 |
| 串联电容 | 沿着等电阻圆(单位圆内,圆心靠右的) | 向逆时针移动 |
| 并联电感 | 沿着等电导圆(单位圆内,圆心靠左的) | 向逆时针移动 |
| 并联电容 | 沿着等电导圆(单位圆内,圆心靠左的) | 向顺时针移动 |
L形匹配网络
最佳功率传输
实现最佳功率传输的常规设计程序一般包括以下几个步骤
1、求出归一化源阻抗和目标阻抗(负载共轭)
在Smith圆图中标记两个阻抗点
2、在Smith圆图中分别过这两个点画出等电阻圆或等电导圆
3、找出第1步和第2步所画出圆的交点
交点的个数=可能存在的L形匹配网络的数目
4、先沿着相应的圆将源阻抗点移动到上述交点,然后再沿相应的圆移动到目标阻抗点,根据这两次移动过程就可以求出电感和电容的归一化值
5、根据给定的工作频率确定电感和电容的实际值
1、在上述步骤中,并不是一定要必需从源阻抗点向负载的共轭复数点移动
也可以将负载阻抗点变换到源阻抗的共轭复数点。
2、由于插入网络总是串并联相间,因此过一个点画等电阻(电导)圆,过另一个点就画等电导(电阻)圆
一般说来
电阻较大的点画等电导圆
电阻较小的点画等电阻圆
例题8.1 教材274页 PDF290页 ★
已知发射机在2GHz频率点的输出阻抗是 Z T = ( 150 + j 75 ) Ω Z_{T}=(150+\mathrm{j} 75) \Omega ZT=(150+j75)Ω
设计一个图8.2所示的L形匹配网络,使输入阻抗为 Z A = ( 75 + j 15 ) Ω Z_{A}=(75+j 15) \Omega ZA=(75+j15)Ω的天线能够得到最大的信号功率

信号源与负载之间实现最大功率传输的条件是信号源阻抗与负载阻抗共轭相等
在这个问题中,即匹配网络的输出阻抗 Z M Z_{M} ZM必须 = 输入阻抗 Z A = ( 75 + j 15 ) Ω Z_{A}=(75+j 15) \Omega ZA=(75+j15)Ω的复数共轭 Z M = Z A ∗ Z_{M}=Z_{A}^{*} ZM=ZA∗★
阻抗 Z M Z_{M} ZM的值 = Z T Z_{T} ZT与电容C并联后再与电感L串联
Z M = 1 Z T − 1 + j B C + j X L = Z A ∗ = ( 75 − j 15 ) Ω Z_{M}=\frac{1}{Z_{T}^{-1}+j B_{C}}+j X_{L}=Z_{A}^{*}=(75-\mathrm{j} 15) \Omega ZM=ZT−1+jBC1+jXL=ZA∗=(75−j15)Ω★
电容C的电纳 B C = ω C B_{C}=\omega C BC=ωC★
电感L的电抗 X L = ω L X_{L}=\omega L XL=ωL★
发射机在2GHz频率点的输出阻抗 Z T = R T + j X T Z_{T}=R_{T}+\mathrm{j} X_{T} ZT=RT+jXT
天线的输入阻抗 Z A = R A + j X A Z_{A}=R_{A}+\mathrm{j} X_{A} ZA=RA+jXA
将发射机阻抗和天线阻抗展开成实部和虚部的形式
R T + j X T 1 + j B C ( R T + j X T ) + j X L = R A − j X A \frac{R_{T}+\mathrm{j} X_{T}}{1+\mathrm{j} B_{C}\left(R_{T}+\mathrm{j} X_{T}\right)}+\mathrm{j} X_{L}=R_{A}-\mathrm{j} X_{A} 1+jBC(RT+jXT)RT+jXT+jXL=RA−jXA
分离上式的实部和虚部,分别写成一个方程,可得
发射极输出阻抗的实部即电阻
R T = R A ( 1 − B C X T ) + ( X A + X L ) B C R T R_{T}=R_{A}\left(1-B_{C} X_{T}\right)+\left(X_{A}+X_{L}\right) B_{C} R_{T} RT=RA(1−BCXT)+(XA+XL)BCRT
发射极输出阻抗的虚部即电抗
X T = R T R A B C − ( 1 − B C X T ) ( X A + X L ) X_{T}=R_{T} R_{A} B_{C}-\left(1-B_{C} X_{T}\right)\left(X_{A}+X_{L}\right) XT=RTRABC−(1−BCXT)(XA+XL)
解出电容C的电纳 B C = ω C B_{C}=\omega C BC=ωC
B C = X T ± R T R A ( R T 2 + X T 2 ) − R T 2 R T 2 + X T 2 B_{C}=\frac{X_{T} \pm \sqrt{\frac{R_{T}}{R_{A}}\left(R_{T}^{2}+X_{T}^{2}\right)-R_{T}^{2}}}{R_{T}^{2}+X_{T}^{2}} BC=RT2+XT2XT±RART(RT2+XT2)−RT2★
由于 R T > R A R_{T}>R_{A} RT>RA,所以根号内的值为正值而且 > X T 2 >X_{T}^{2} >XT2
为了确保电容C的电纳 B C > 0 B_{C}>0 BC>0,必须选取式(8.4)中的“正”号
B C = X T + R T R A ( R T 2 + X T 2 ) − R T 2 R T 2 + X T 2 B_{C}=\frac{X_{T} + \sqrt{\frac{R_{T}}{R_{A}}\left(R_{T}^{2}+X_{T}^{2}\right)-R_{T}^{2}}}{R_{T}^{2}+X_{T}^{2}} BC=RT2+XT2XT+RART(RT2+XT2)−RT2
将式(8.4)代入式(8.3a)可得电感L的电抗 X L = ω L X_{L}=\omega L XL=ωL
X L = 1 B C − R A ( 1 − B C X T ) B C R T − X A X_{L}=\frac{1}{B_{C}}-\frac{R_{A}\left(1-B_{C} X_{T}\right)}{B_{C} R_{T}}-X_{A} XL=BC1−BCRTRA(1−BCXT)−XA★
代入已知数据,可求得
电容C的电纳 B C = 9.2 m S ⇒ C = B C / ω = 0.73 p F B_{C}=9.2 \mathrm{mS} \Rightarrow C=B_{C} / \omega=0.73 \mathrm{pF} BC=9.2mS⇒C=BC/ω=0.73pF
电感L的电抗 X L = 76.9 Ω ⇒ L = X L / ω = 6.1 n H X_{L}=76.9 \Omega \Rightarrow L=X_{L} / \omega=6.1 \mathrm{nH} XL=76.9Ω⇒L=XL/ω=6.1nH
例题8.2 教材276页 PDF292页 ★
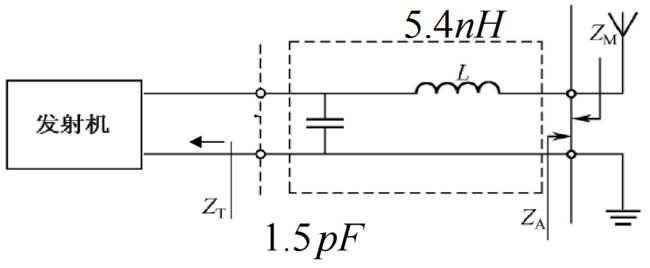
已知晶体管在1.5GHz频率点的输出阻抗是 Z T = ( 100 + j 50 ) Ω {Z_{\rm{T}}} = (100 + {\rm{j}}50)\Omega ZT=(100+j50)Ω
请设计一个如图所示的L形匹配网络,使输入阻抗为 Z A = ( 50 + j 10 ) Ω {Z_{\rm{A}}} = (50 + {\rm{j}}10)\Omega ZA=(50+j10)Ω的天线能够得到最大功率
解:首先计算归一化阻抗,假设特征阻抗=50欧姆
特征阻抗可以任意设定,计算方便就行
Z 0 = 50 Ω {Z_0} = 50\Omega Z0=50Ω, Y 0 = 0.02 Ω − 1 {Y_0} = 0.02{\Omega ^{ - 1}} Y0=0.02Ω−1
归一化输出阻抗 z T = Z T / Z 0 = ( 100 + j 50 ) / 50 = 2 + j {z_{\rm{T}}} = {Z_{\rm{T}}}/{Z_0} =(100 + {\rm{j}}50)/50 = 2 + {\rm{j}} zT=ZT/Z0=(100+j50)/50=2+j
归一化输出导纳 y T = 1 / z T = 0.4 − j 0.2 {y_T} = 1/{z_{\rm{T}}}=0.4 - j0.2 yT=1/zT=0.4−j0.2
归一化输入阻抗的共轭 z M = z A ∗ = Z A ∗ / Z 0 = ( 50 − j 10 ) / 50 = 1 − j 0.2 {z_{\rm{M}}} = z_{\rm{A}}^ * ={{Z_A^ * }}/{{{Z_0}}} = (50 - {\rm{j}}10)/50 = 1 - {\rm{j}}0.2 zM=zA∗=ZA∗/Z0=(50−j10)/50=1−j0.2
归一化输入导纳的共轭 y M = 1 / z M = 0.92 + j 0.19 {y_M} = 1/{z_{\rm{M}}} = 0.92 + j0.19 yM=1/zM=0.92+j0.19
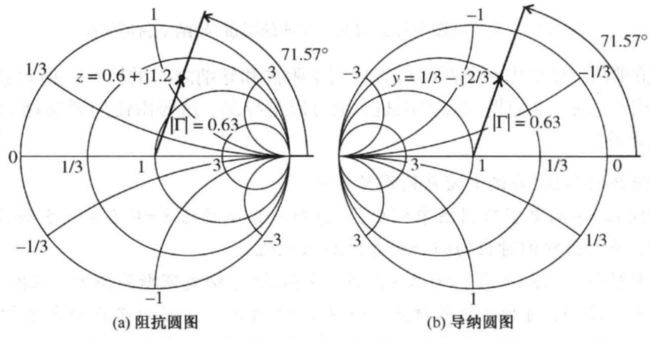
归一化交点阻抗 z T C = 1 − j 1.22 {z_{{\rm{TC}}}} = 1 - {\rm{j}}1.22 zTC=1−j1.22
和归一化输入阻抗的共轭 z M {z_{\rm{M}}} zM等电阻
归一化交点导纳 y T C = 0.4 + j 0.49 {y_{{\rm{TC}}}} = 0.4 + {\rm{j}}0.49 yTC=0.4+j0.49
和归一化输出阻抗 z T {z_{\rm{T}}} zT等电导
由图可知,归一化输出阻抗 z T = 2 + j {z_T} = 2 + j zT=2+j→
归一化交点阻抗 z T C = 1 − j 1.22 {z_{{\rm{TC}}}} = 1 - {\rm{j}}1.22 zTC=1−j1.22→
归一化输入阻抗的共轭 z M = 1 − j 0.2 {z_M} = 1 - j0.2 zM=1−j0.2
先沿着等电导圆向顺时针移动,所以先并联电容
再沿着等电阻圆向顺时针移动,所以再串联电感
归一化电容→归一化交点导纳 - 归一化输出导纳 末-初
归一化电容 j b C = y T C − y T = j 0.69 = j ω C / Y 0 {\rm{j}}{b_{\rm{C}}} = {y_{{\rm{TC}}}} - {y_{\rm{T}}} = {\rm{j}}0.69= {{j\omega C}}/{{{Y_0}}} jbC=yTC−yT=j0.69=jωC/Y0★
归一化电感→归一化输入阻抗的共轭 - 归一化交点阻抗 末-初
归一化电感 j x L = z A − z T C = j 1.02 = j ω L / Z 0 {\rm{j}}{x_{\rm{L}}} = {z_{\rm{A}}} - {z_{{\rm{TC}}}} = {\rm{j}}1.02= {{j\omega L}}/{{{Z_0}}} jxL=zA−zTC=j1.02=jωL/Z0★
实际电容 C = Y 0 b C ω = 0.02 × 0.69 2 π × 1.5 × 10 9 = 1.5 × 1 0 − 12 = 1.5 p F C = \frac{{{Y_0}{b_{\rm{C}}}}}{\omega } = \frac{{0.02 \times 0.69}}{{2\pi \times 1.5 \times {{10}^9}}} = 1.5 \times {10^{ - 12}} = 1.5pF C=ωY0bC=2π×1.5×1090.02×0.69=1.5×10−12=1.5pF
实际电感 L = Z 0 x L ω = 50 × 1.02 2 π × 1.5 × 10 9 = 5.4 × 1 0 − 9 = 5.4 n H L = \frac{{{Z_0}{x_{\rm{L}}}}}{\omega } = \frac{{50 \times 1.02}}{{2\pi \times 1.5 \times {{10}^9}}} = 5.4 \times {10^{ - 9}} = 5.4nH L=ωZ0xL=2π×1.5×10950×1.02=5.4×10−9=5.4nH
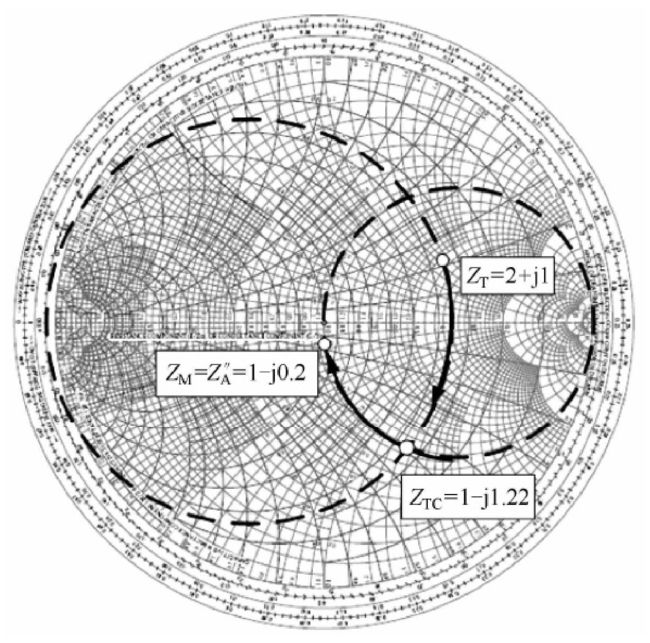
从Smith图上可以看到,两圆之间还有一个交点
通过这个交点也可以进行阻抗匹配
具体选用哪种网络,可根据其它条件而定
如高低通特性,元件值的合理性等等
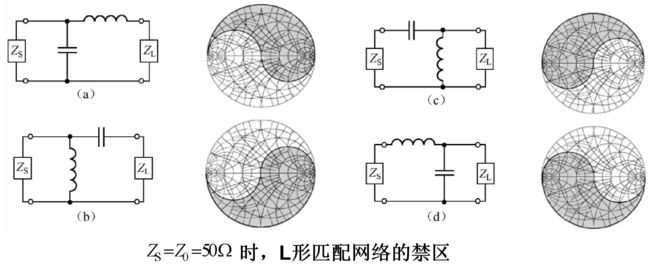
8.1.2 匹配禁区 教材280页 PDF296页
Smith圆图的匹配禁区:网络拓扑无法在任何负载阻抗和源阻抗之间实现预期的匹配。
由于 Z S = 50 Z_S=50 ZS=50,匹配从圆图的中心点开始,到达 Z L ∗ Z_L^* ZL∗
可以看出,如果 Z L Z_L ZL在阴影区中,那么 Z L ∗ Z_L^* ZL∗和 Z L Z_L ZL关于 Γ \Gamma Γ平面的实轴对称,从从圆图的中心点开始,无法到达 Z L ∗ Z_L^* ZL∗,该匹配网络不能匹配该负载★★
| ★★★ | 源阻抗 | |
|---|---|---|
| 串联电感 | 沿着等电阻圆(单位圆内,圆心靠右的) | 向顺时针移动 |
| 串联电容 | 沿着等电阻圆(单位圆内,圆心靠右的) | 向逆时针移动 |
| 并联电感 | 沿着等电导圆(单位圆内,圆心靠左的) | 向逆时针移动 |
| 并联电容 | 沿着等电导圆(单位圆内,圆心靠左的) | 向顺时针移动 |
5.3 LC串并联谐振回路
(1)串并联支路阻抗变换

1 R P + 1 j X P = 1 r S + j X S = r S − j X S r S 2 + X S 2 \frac{1}{{{R_P}}} + \frac{1}{{j{X_P}}} = \frac{1}{{{r_S} + j{X_S}}} = \frac{{{r_S} - j{X_S}}}{{r_S^2 + X_S^2}} RP1+jXP1=rS+jXS1=rS2+XS2rS−jXS
实部相等:
R P = r s 2 + x s 2 r s = r s ( 1 + ( x s r s ) 2 ) = r s ( 1 + Q 2 ) {R_P} = \frac{{r_s^2 + x_s^2}}{{{r_s}}} = {r_s}(1 + {(\frac{{{x_s}}}{{{r_s}}})^2}) = {r_s}(1 + {Q^2}) RP=rsrs2+xs2=rs(1+(rsxs)2)=rs(1+Q2)
串联支路
Q = x s r s Q = \frac{{{x_s}}}{{{r_s}}} Q=rsxs
虚部相等:
X P = r s 2 + x s 2 x s = x s ( 1 + ( r s x s ) 2 ) = x s ( 1 + 1 Q 2 ) {X_P} = \frac{{r_s^2 + x_s^2}}{{{x_s}}} = {x_s}(1 + {(\frac{{{r_s}}}{{{x_s}}})^2}) = {x_s}(1 + \frac{1}{{{Q^2}}}) XP=xsrs2+xs2=xs(1+(xsrs)2)=xs(1+Q21)
并联支路
Q = R P X P Q = \frac{{{R_P}}}{{{X_P}}} Q=XPRP
两者相等
Q = x s r s = R P X P Q = \frac{{{x_s}}}{{{r_s}}} = \frac{{{R_P}}}{{{X_P}}} Q=rsxs=XPRP
L型阻抗匹配网络计算分析
特征:① 两电抗元件组成:结构形式同 L
② 窄带网络:两电抗元件不同性质,有选频滤波性能
讨论问题:1. 已知工作频率 ω 0 {\omega _0} ω0,欲将 R L {R_L} RL变换为 R S {R_S} RS
求:电路结构和 X S {X_S} XS、 X P {X_P} XP
2. L 网络的带宽
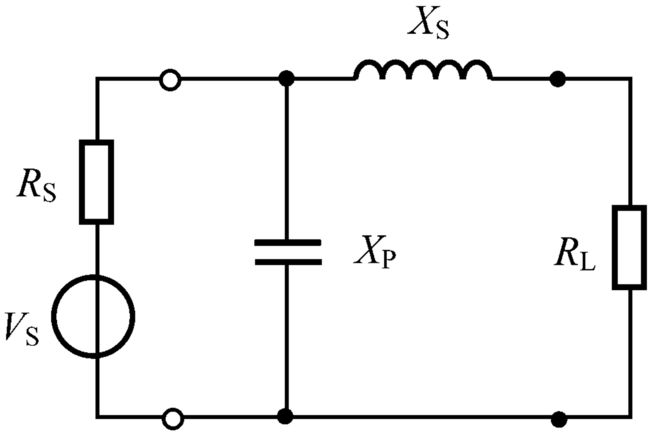
当 R S > R L {R_S}>{R_L} RS>RL时, Q = R S / R L − 1 Q = \sqrt {{R_S}/{R_L} - 1} Q=RS/RL−1★
L网络串联支路电抗 X S = Q R L {X_S} = Q{R_L} XS=QRL★
L网络并联支路电抗 X P = R S / Q {X_P} = {R_S}/{Q} XP=RS/Q★
串联支路电抗 X S {X_S} XS = 附近的 R S {R_S} RS或 R L {R_L} RL × \times ×Q ★
并联支路电抗 X P {X_P} XP = 附近的 R S {R_S} RS或 R L {R_L} RL / Q ★
已知工作频率 ω 0 {\omega _0} ω0
可得电感L、电容C
Q = R ( 大 值 ) / R ( 小 值 ) − 1 Q = \sqrt {{R_{(大值)}}/{R_{(小值)}} - 1} Q=R(大值)/R(小值)−1★
L 网络缺点: 当两个要阻抗变换的源和负载电阻值确定后,L网络的 Q 值也确定了,是不能选择的,因此该窄带网络的滤波性能不能选择
例题
已知信号源内阻 R S {R_S} RS=12 ,并串有寄生电感L = 1.2
负载电阻 R L {R_L} RL=58 并带有并联的寄生电容 = 1.8PF,工作频率为f
设计 L 匹配网络,使信号源与负载达匹配
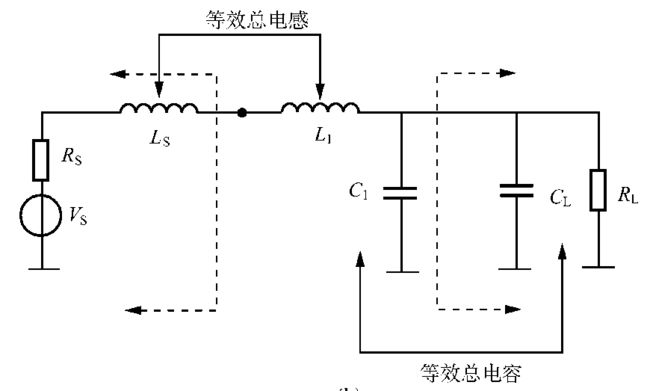
先将信号源端的寄生电感和负载端的寄生电容归并到 L 网络中
当 R L > R S {R_L}>{R_S} RL>RS时, Q = R L / R S − 1 Q = \sqrt {{R_L}/{R_S} - 1} Q=RL/RS−1★
L网络串联支路电抗 X S = Q R S = 1.96 × 12 = 23.5 Ω {X_S} = Q{R_S} = 1.96 \times 12 = 23.5\Omega XS=QRS=1.96×12=23.5Ω★
L S ′ = L S + L 1 {L'_S} = {L_S} + {L_1} LS′=LS+L1★
L网络并联支路电抗 X P = R L / Q = 58 1.96 = 29.6 Ω {X_P} = {R_L}/{Q} = \frac{{58}}{{1.96}} = 29.6\Omega XP=RL/Q=1.9658=29.6Ω★
C P = C 1 + C L {C_P} = {C_1} + {C_L} CP=C1+CL★
8.1.3 T形匹配网络和π形匹配网络
L形匹配网络元件较少,很难同时满足匹配和Q值得要求,需要更多的器件,以提供更多的选择方案
一般匹配网络的器件扩展原则是串并交替
因此从L形进行一元件扩展得到T形或Π形匹配网络。
T形匹配网络 教材285页 PDF301页 例8.5
设计一个T形匹配网络,要求该网络将 Z L = ( 60 − j 30 ) Ω {Z_{\rm{L}}} = (60 - {\rm{j}}30)\Omega ZL=(60−j30)Ω的负载 阻抗变换成 的输入阻抗,且最大节点品质因数等于3
假设工作频率 ,计算匹配网络的元件值。
π形匹配网络 教材286页 PDF302页 例8.6
5.4 微带线匹配网络
工作频率的提高导致工作波长的减小,分立元件的寄生参数效应变得明显,分布参数元件就代替了分立元件得到广泛应用
5.4.1 从分立元件到微带线
在中间过渡频段(例如几吉赫兹到几十吉赫兹),可以采用分立元件和分布参数元件混合使用的方法。
从拓扑结构上讲,这种匹配方案用微带传输线代替电感以解决高频实现的问题
从图形概念上讲,是用驻波比圆代替等电阻圆作图
教材288页 PDF304页 例8.7
首先归一化阻抗,在Smith圆图上标出两阻抗点
分别通过ZL和Zin画两个驻波比圆
选择与两圆都相交的等电导线作为过渡,确定A、B两点
ZL与A两点的夹角计算传输线长度l1
注意:内圈和外圈刻度最左边是起点,递增的方向相反,一圈=0.5
传输线的电长度l = 两点之间顺时针转过的圆弧对应的刻度 × λ \times \lambda ×λ
A、B两点导纳增量计算电容量
B与Zin之间的夹角计算传输线长度l2
8.2.2
传输线(微带线)加上电容的匹配方案几乎可以匹配任何网络
但电容器件必须是标准容值的电容,可变性不好
根据短路或开路传输线的输入阻抗有电感或电容的特性:
Z i n = Z 0 Z L + j Z 0 t g β d Z 0 + j Z L t g β d { Z L = 0 ; Z i n = j Z 0 t g β d Z L → ∞ ; Z i n = − j Z 0 c t g β d {Z_{in}} = {Z_0}\frac{{{Z_L} + j{Z_0}tg\beta d}}{{{Z_0} + j{Z_L}tg\beta d}}{\rm{ }}\left\{ \begin{array}{l} {Z_L} = 0;{\rm{ }}{Z_{in}} = j{Z_0}tg\beta d\\ {Z_L} \to \infty ;{\rm{ }}{Z_{in}} = {\rm{ - }}j{Z_0}ctg\beta d \end{array} \right. Zin=Z0Z0+jZLtgβdZL+jZ0tgβd{ZL=0;Zin=jZ0tgβdZL→∞;Zin=−jZ0ctgβd
如果用它们代替电感或电容,便构成短截线匹配网络
电感电容值由传输线传输常数和线长度所确定,从而解决调谐问题
短截线匹配的思想:
以网络输入端为参考,匹配可以分两个部分来考虑。
1、实部匹配,传输线完成
2、虚部匹配,串并联短截线完成
3、计算方法:
并联短截线,用导纳计算
串联短截线,用阻抗计算
工作原理
实部匹配
t = t g β d t = tg\beta d t=tgβd
Z L = R L + j X L {Z_L} = {R_L} + j{X_L} ZL=RL+jXL
Y L = G L + j B L {Y_L} = {G_L} + j{B_L} YL=GL+jBL
Z i n = Z 0 Z L + j Z 0 t g β d Z 0 + j Z L t g β d {Z_{in}} = {Z_0}\frac{{{Z_L} + j{Z_0}tg\beta d}}{{{Z_0} + j{Z_L}tg\beta d}} Zin=Z0Z0+jZLtgβdZL+jZ0tgβd
Y i n = Y 0 Y L + j Y 0 t g β d Y 0 + j Y L t g β d {Y_{in}} = {Y_0}\frac{{{Y_L} + j{Y_0}tg\beta d}}{{{Y_0} + j{Y_L}tg\beta d}} Yin=Y0Y0+jYLtgβdYL+jY0tgβd
以并联短截线为例
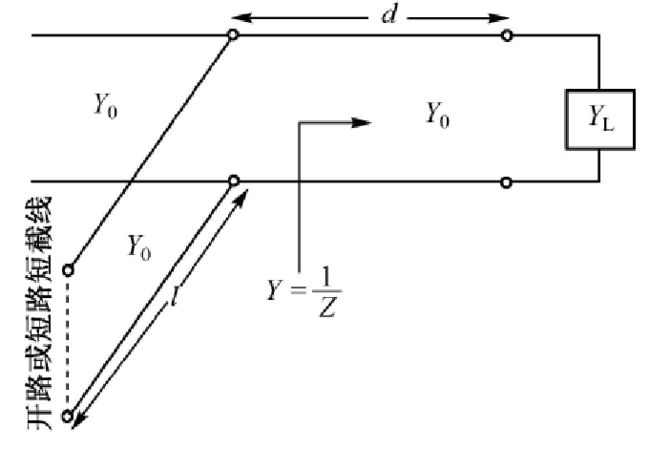
Z i n = Z 0 Z L + j Z 0 t g β d Z 0 + j Z L t g β d = Z 0 R L + j ( Z 0 t + X L ) ( Z 0 − X L t ) + j R L t {Z_{in}} = {Z_0}\frac{{{Z_L} + j{Z_0}tg\beta d}}{{{Z_0} + j{Z_L}tg\beta d}} = {Z_0}\frac{{{R_L} + j\left( {{Z_0}t + {X_L}} \right)}}{{\left( {{Z_0} - {X_L}t} \right) + j{R_L}t}} Zin=Z0Z0+jZLtgβdZL+jZ0tgβd=Z0(Z0−XLt)+jRLtRL+j(Z0t+XL)
Y i n = 1 Z 0 × ( Z 0 − X L t ) + j R L t R L + j ( Z 0 t + X L ) {Y_{in}} = \frac{1}{{{Z_0}}} \times \frac{{\left( {{Z_0} - {X_L}t} \right) + j{R_L}t}}{{{R_L} + j\left( {{Z_0}t + {X_L}} \right)}} Yin=Z01×RL+j(Z0t+XL)(Z0−XLt)+jRLt
G i n = R e ( Y i n ) = R L ( 1 + t 2 ) R L 2 + ( Z 0 t + X L ) 2 {G_{in}}{\rm{ = }}{\mathop{\rm Re}\nolimits} \left( {{Y_{in}}} \right) = \frac{{{R_L}\left( {1 + {t^2}} \right)}}{{R_L^2 + {{\left( {{Z_0}t + {X_L}} \right)}^2}}} Gin=Re(Yin)=RL2+(Z0t+XL)2RL(1+t2)
B i n = I m ( Y i n ) = R L 2 t + ( Z 0 t + X L ) ( X L t − Z 0 ) Z 0 [ R L 2 + ( Z 0 t + X L ) 2 ] {B_{in}}{\rm{ = }}{\mathop{\rm Im}\nolimits} \left( {{Y_{in}}} \right) = \frac{{R_L^2t + \left( {{Z_0}t + {X_L}} \right)\left( {{X_L}t - {Z_0}} \right)}}{{{Z_0}\left[ {R_L^2 + {{\left( {{Z_0}t + {X_L}} \right)}^2}} \right]}} Bin=Im(Yin)=Z0[RL2+(Z0t+XL)2]RL2t+(Z0t+XL)(XLt−Z0)
实部匹配方法一
取适当的 t 值,使其达到
R e ( Y S ) = R e ( Y i n ) = R L ( 1 + t 2 ) R L 2 + ( Z 0 t + X L ) 2 {\mathop{\rm Re}\nolimits} ({Y_S}) = {\mathop{\rm Re}\nolimits} \left( {{Y_{in}}} \right) = \frac{{{R_L}\left( {1 + {t^2}} \right)}}{{R_L^2 + {{\left( {{Z_0}t + {X_L}} \right)}^2}}} Re(YS)=Re(Yin)=RL2+(Z0t+XL)2RL(1+t2)
Y S = R L ( 1 + t 2 ) R L 2 + ( Z 0 t + X L ) 2 {Y_S} = \frac{{{R_L}\left( {1 + {t^2}} \right)}}{{R_L^2 + {{\left( {{Z_0}t + {X_L}} \right)}^2}}} YS=RL2+(Z0t+XL)2RL(1+t2)
得到t
d λ = 1 2 π t g − 1 t , t > 0 \frac{d}{\lambda } = \frac{1}{{2\pi }}t{g^{ - 1}}t,{\rm{ t > 0}} λd=2π1tg−1t,t>0
d λ = 1 2 π ( π + t g − 1 t ) , t < 0 \frac{d}{\lambda } = \frac{1}{{2\pi }}\left( {\pi + t{g^{ - 1}}t} \right),{\rm{ t < 0}} λd=2π1(π+tg−1t),t<0
实部匹配方法二
令 t → ∞ t \to \infty t→∞于是 d = λ / λ 4 4 d = {\lambda \mathord{\left/ {\vphantom {\lambda 4}} \right.} 4} d=λ/λ44
令传输线阻抗为 Z 0 L Z_{0L} Z0L
R e ( Y i n ) = lim t → ∞ R L ( 1 + t 2 ) R L 2 + ( Z 0 L t + X L ) 2 = R L Z 0 L 2 {\mathop{\rm Re}\nolimits} \left( {{Y_{in}}} \right) = \mathop {\lim }\limits_{t \to \infty } \frac{{{R_L}\left( {1 + {t^2}} \right)}}{{R_L^2 + {{\left( {{Z_{0L}}t + {X_L}} \right)}^2}}} = \frac{{{R_L}}}{{Z_{0L}^2}} Re(Yin)=t→∞limRL2+(Z0Lt+XL)2RL(1+t2)=Z0L2RL
I m ( Y i n ) = lim t → ∞ R L 2 t + ( Z 0 L t + X L ) ( X L t − Z 0 L ) Z 0 L [ R L 2 + ( Z 0 L t + X L ) 2 ] = X L Z 0 L 2 {\mathop{\rm Im}\nolimits} \left( {{Y_{in}}} \right) = \mathop {\lim }\limits_{t \to \infty } \frac{{R_L^2t + \left( {{Z_{0L}}t + {X_L}} \right)\left( {{X_L}t - {Z_{0L}}} \right)}}{{{Z_{0L}}\left[ {R_L^2 + {{\left( {{Z_{0L}}t + {X_L}} \right)}^2}} \right]}} = \frac{{{X_L}}}{{Z_{0L}^2}} Im(Yin)=t→∞limZ0L[RL2+(Z0Lt+XL)2]RL2t+(Z0Lt+XL)(XLt−Z0L)=Z0L2XL
改变参数Z0,使 Y S = R L Z 0 L 2 {Y_S} = \frac{{{R_L}}}{{Z_{0L}^2}} YS=Z0L2RL
虚部匹配
确定实部匹配后,虚部为一固定值,并联或串联短截线后使
− B S = I m ( Y i n ) + B - {B_S} = {\mathop{\rm Im}\nolimits} \left( {{Y_{in}}} \right) + B −BS=Im(Yin)+B
B为并联短截线电纳
B = − [ I m ( Y i n ) + B S ] B = - \left[ {{\mathop{\rm Im}\nolimits} \left( {{Y_{in}}} \right) + {B_S}} \right] B=−[Im(Yin)+BS]
短截线长度
开路线
l λ = { 1 2 π t g − 1 B Y 0 , B > 0 1 2 π [ π − t g − 1 B Y 0 ] , B < 0 \frac{l}{\lambda } = \left\{ \begin{array}{l} \frac{1}{{2\pi }}t{g^{ - 1}}\frac{B}{{{Y_0}}},B > 0\\ \frac{1}{{2\pi }}\left[ {\pi - t{g^{ - 1}}\frac{B}{{{Y_0}}}} \right],B < 0 \end{array} \right. λl={2π1tg−1Y0B,B>02π1[π−tg−1Y0B],B<0
短路线
l λ = { 1 2 π c t g − 1 B Y 0 , B < 0 1 2 π [ π − c t g − 1 B Y 0 ] , B > 0 \frac{l}{\lambda } = \left\{ \begin{array}{l} \frac{1}{{2\pi }}ct{g^{ - 1}}\frac{B}{{{Y_0}}},B < 0\\ \frac{1}{{2\pi }}\left[ {\pi - ct{g^{ - 1}}\frac{B}{{{Y_0}}}} \right],B > 0 \end{array} \right. λl={2π1ctg−1Y0B,B<02π1[π−ctg−1Y0B],B>0
串联短截线
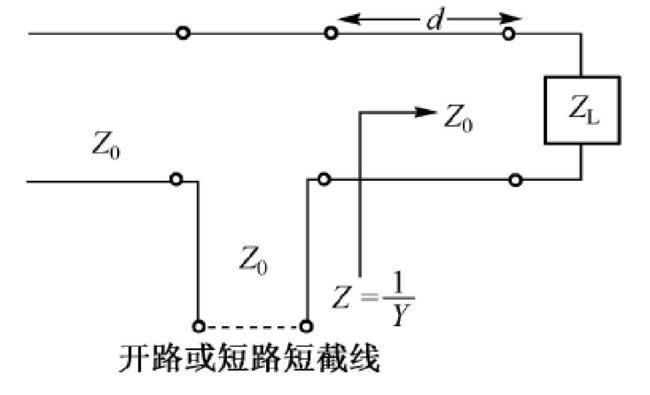
注意:
如果用解析法求解,传输线与短截线的特征阻抗可以任意选择
可以相同,也可以不同。
但是,如果用Smith圆图求解,所有归一化变量所用的特征阻抗必须相同。
例匹配网络的拓扑结构如图

假设负载ZL=100-j20,源端输出阻抗为ZS=32-j24。确定匹配电路参数。
向左看阻抗为ZS=32-j24,要达到阻抗匹配,需连接阻抗为Zin=32+j24,即导纳为Yin=0.02-j0.015
右端传输线长为
短截线导纳为
用短路连接线,特征阻抗Z0k可选
单节短截线图解法
假设源端的阻抗为Z0,则只需将负载匹配到Z0即可
并联短截线采用导纳图求解
串联短截线采用阻抗图求解
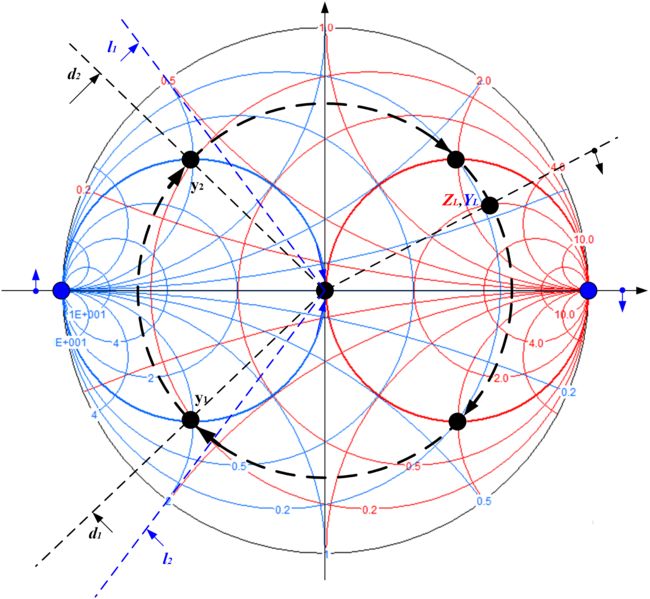
例:给定负载阻抗为ZL=100+j132,匹配到特征阻抗=50欧姆
1)首先归一化阻抗 ,在Smith圆图上标出该点
Z L / Z 0 = 2 + j 2.64 {{{Z_L}}}/{{{Z_0}}} = 2 + j2.64 ZL/Z0=2+j2.64
Γ Z L = 0.707 ∠ 25. 9 ∘ {\Gamma _{{Z_L}}} = 0.707\angle {25.9^ \circ } ΓZL=0.707∠25.9∘
2)过该点在Smith圆图画出对应的SWR圆
3)找到SWR圆与1电导圆(1电阻圆)的交点(两个)
Γ y 1 = 0.707 ∠ − 13 5 ∘ {\Gamma _{y1}} = 0.707\angle - {135^ \circ } Γy1=0.707∠−135∘
Γ y 2 = 0.707 ∠ + 13 5 ∘ {\Gamma _{y2}} = 0.707\angle + {135^ \circ } Γy2=0.707∠+135∘
4)求出电纳(电抗)值
5)由负载向源方向求出传输线长
d 1 = 0.223 λ {d_1} = 0.223\lambda d1=0.223λ、 d 2 = 0.348 λ {d_2} = 0.348\lambda d2=0.348λ
6)确定短截线形式(开、短路)
7)从负载到源方向读出短截线长
采用短路短截线
l 1 = 0.074 λ {l_1} = 0.074\lambda l1=0.074λ、 l 2 = 0.426 λ {l_2} = 0.426\lambda l2=0.426λ
采用开路短截线
l 1 = 0.324 λ {l_1} = 0.324\lambda l1=0.324λ、 l 2 = 0.176 λ {l_2} = 0.176\lambda l2=0.176λ
作业
《射频电路设计——理论与应用》
第三章中习题:3.1,3.8,3.11,3.20, 3.27,3.30
第八章中习题 :8.3,8.5,8.10,8.15,8.17