pytorch深度学习（5）反向传播
目录
1. 简单神经网络中的梯度：
2. 复杂的神经网络
3.反向传播（Backpropagation）
3.1（具体例子）
3.2 The composition of functions and Chain Rule（链式法则）
练习
4.tensor in pytorch
代码实现：
练习
1. 简单神经网络中的梯度：
简单模型，我们可以通过简单的解析式去完成，但对于一些复杂的模型，我们该如何处理呢？
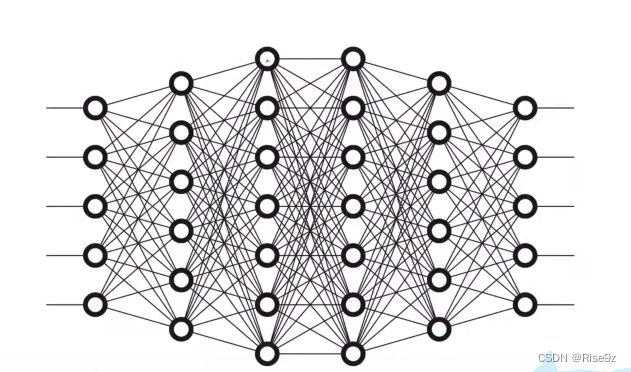
2. 复杂的神经网络
图中每一个圈内都存在一个权重 w
我们假设每一列都代表一层神经网络，可知第一层是5维的向量，第二层是6维的向量，所以要将第一层输出到第二层，我们就需要一个6行5列（6*5）的权重 w（30） h [6*1] = w [6*5] * x [5*1]
以此类推，第二层到第三层就需要一个7行6列（7*6）的权重 w （42个）
如果要像前面那样写解析式的话，要写上百个，基本是不太可能了。
我们要引入一种新的算法：反向传播算法
3.反向传播（Backpropagation）
我们先来了解一下反向传播的定义：是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。
3.1（具体例子）
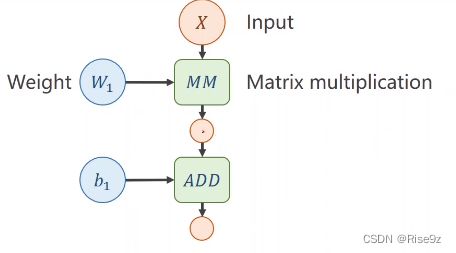
3.1.1一个两层的神经网络：
全连接神经网络中的一个层（第一层）
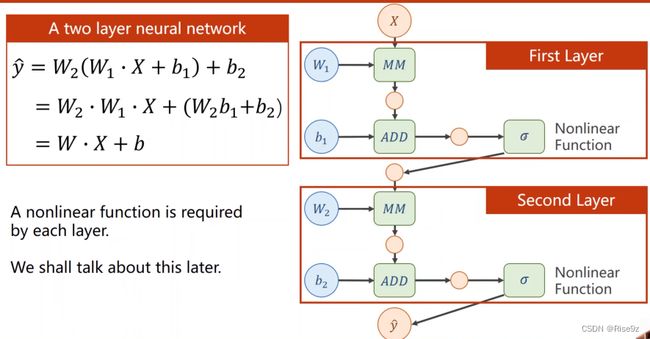
（第二层）
当然，上面的式子可以被进行化简（如下），但这样做使得层数多和层数少变得没有区别，失去它原本分层的意义。
3.2.2那如何解决这个问题呢？(提高模型的复杂程度)
我们对每一层最终的输出，加一个非线性的变化函数，使得第一层无法展开，而去与第二层融合。
3.2 The composition of functions and Chain Rule（链式法则）
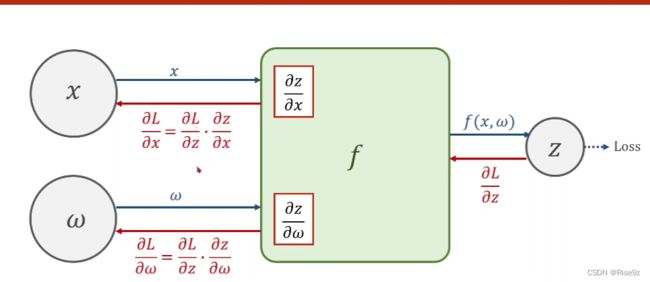
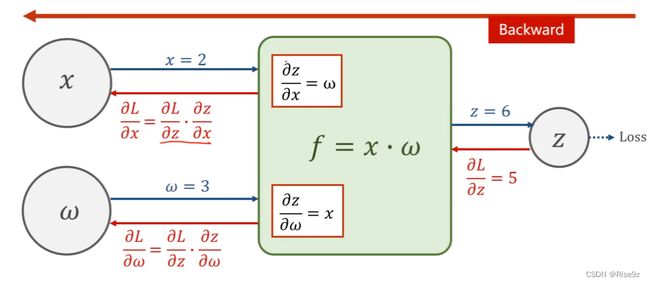
把网络看成一个图，在图上传播梯度，然后根据链式法则把梯度求出来。反向传播算法权重可以是权重矩阵，偏置通常定义成向量形式。
3.2.1具体过程：
首先，我们通过前馈传播,沿着上图蓝色的箭头去计算loss（损失函数的值）
接着，我们再往回进行反向传播，我们拿到了Loss对z的偏导，
再然后，我们通过链式法则，继续向前求得对w（对x）的导数。
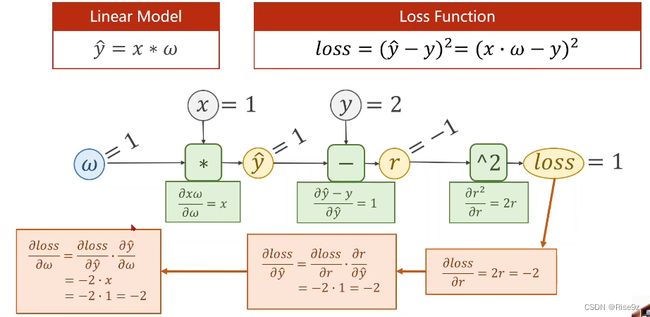
3.2.2例子
前馈传播：
反向传播：
Linear Model（完整计算过程）
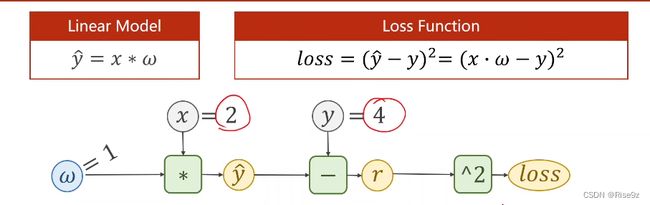
练习
（1） 改变一下x，y ，尝试求解Loss对w的偏导
（2）加一个b，尝试求解Loss对w的偏导以及Loss对b的偏导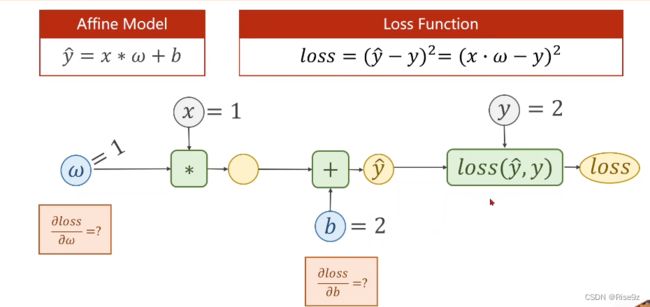
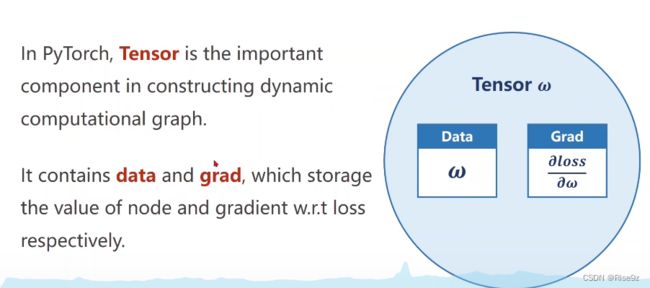
4.tensor in pytorch
代码实现：
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0])
w.requires_grad = True # 默认不计算，只有当需要梯度的时候才会计算
# 定义模型
def forward(x):
return x * w # x会转换成tensor
# 定义损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2 # 实际上是构建计算图的过程
print("predict (before training)", 4, forward(4).item())
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x, y) # 前向传播，计算损失
l.backward() # 向后传播，计算梯度
print('\tgrad:', x, y, w.grad.item()) # 使用item变成标量，不会产生计算图
w.data = w.data - 0.01 * w.grad.data # 进行权重更新的时候不能使用tensor,取data是不会产生计算图
w.grad.data.zero_() # .backward()计算的梯度会累加，注意把梯度清零
print("progress:", epoch, l.item())
print("predict (after training)", 4, forward(4).item())
效果图如下：
练习
尝试一下求二次的模型