多标签分类评价指标HL，RL，OE， Cov的计算及Python实现

AP的计算见本人另一篇博客
HL，RL， OE， Cov是多标签分类的评价指标，通常越小表明模型越好。

一，HL计算
公式：

大意是，有N个样本的数据集，对每个样本的标签集部分，计算真实标签与预测标签部分有多少个不同的部分，
举个栗子：
样本1，y_true = [1, 0, 1, 0, 0]，y_pred = [0, 1, 1, 0, 0]，可以看到它有2个预测出错的部分，记样本1汉明损失为2/5 = 0.4
样本2，y_true = [1, 0, 1, 0, 1]，y_pred = [1, 1, 0, 0, 0]，可以看到它有3个预测出错的部分，记样本1汉明损失为3/5 = 0.6
对于总的样本集，汉明损失为（0.4+0.6）/ 2 = 0.5
程序：

import numpy as np
from sklearn import metrics
label = np.array([[1, 0, 1, 0, 0], [1, 0, 1, 0, 1]])
pred = np.array([[0, 1, 1, 0, 0], [1, 1, 0, 0, 0]])
print(metrics.hamming_loss(label, pred))

结果：

二，RL计算
公式：

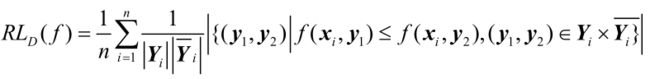
这一大坨我估计很多人第一眼看到就不想看第二眼，

翻译成人话，就是计算标签集中的排序损失。假设数据集有N个样本，对每个样本计算它的标签集中为1的标签的概率小于标签集中为0的概率的标签个数除以标签为1的标签个数乘以标签为0的标签个数。
举个栗子：
样本1，真实标签集y_true = [1, 0, 1, 0, 0]，标签预测概率值y_score = [0.3, 0.4, 0.5, 0.1, 0.15]，样本1有2个预测为1的标签，即概率为0.3和概率为0.5的标签，一个个来看，对概率为0.3的标签，在整个标签集中，标签为0的标签中，有概率为0.4的标签概率比它大，记为1；对概率为0.5的标签，在整个标签集中，标签为0的标签中，没有标签的概率值比它大，记为0。则样本1的所有标签的排序损失标签为1个，标签为1的标签有2个，标签为0的标签有3个，则基数对有2*3=6个，样本的排序损失为1/6=0.1666667

样本2，真实标签集y_true = [1, 0, 1, 0, 1]，标签预测概率值y_score = [0.4, 0.5, 0.7, 0.2, 0.6]，样本1有3个预测为1的标签，即概率为0.4、概率为0.7和概率为0.7的标签，一个个来看，对概率为0.4的标签，在整个标签集中，标签为0的标签中，有概率为0.5的标签概率比它大，记为1；对概率为0.7的标签，没有标签的概率值比它大，记为0；对概率为0.6的标签，没有标签的概率值比它大，记为0。则样本1的所有标签的排序损失标签为1个，标签为1的标签有2个，标签为0的标签有3个，则基数对有2*3=6个，样本的排序损失为1/6=0.1666667

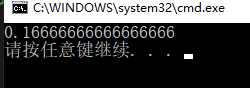
数据集总的排序损失为：（0.16667+0.16667）/ 2 = 0.16667
程序：

label = np.array([[1, 0, 1, 0, 0], [1, 0, 1, 0, 1]])
logit = np.array([[0.3, 0.4, 0.5, 0.1, 0.15], [0.4, 0.5, 0.7, 0.2, 0.6]])
print(metrics.label_ranking_loss(label, logit))

结果：

三，OE计算
公式：

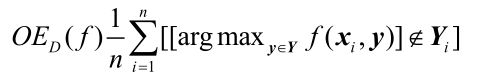
这个就是计算每个样本标签集中概率最大的那个标签在不在标签为1的部分里面，在，记为0，不在，则记为1。就是说最大的那个标签预测的对不对。
举个栗子：
样本1，真实标签集y_true = [1, 0, 1, 0, 0]，标签预测概率值y_score = [0.3, 0.4, 0.5, 0.1, 0.15]，概率最大的标签对应的真实标签为1，记为0。
样本2，真实标签集y_true = [1, 0, 1, 0, 1]，标签预测概率值y_score = [0.4, 0.5, 0.7, 0.2, 0.6]，概率最大的标签对应的真实标签为1，记为0。
总的错误率就等于 （0+0）/ 2 = 0

程序：

def One_error(label, logit):
    N = len(label)
    for i in range(N):
        if max(label[i]) == 0:
            print("该条数据哪一类都不是")
    label_index = []
    for i in range(N):
        index = np.where(label[i] == 1)[0]
        label_index.append(index)
    OneError = 0
    for i in range(N):
        if np.argmax(logit[i]) not in label_index[i]:
            OneError += 1
    OneError = OneError * 1.0 / N
    return OneError

label = np.array([[1, 0, 1, 0, 0], [1, 0, 1, 0, 1]])
logit = np.array([[0.3, 0.4, 0.5, 0.1, 0.15], [0.4, 0.5, 0.7, 0.2, 0.6]])
print(One_error(label, logit))

结果：

四，Cov计算
公式：

这个就是计算每个样本的标签集中，按照概率从大到小排列，到排多少的时候能把标签为1的标签覆盖完毕。为啥要减1，是因为排序是从1开始的。
举个栗子：
样本1，真实标签集y_true = [1, 0, 1, 0, 0]，标签预测概率值y_score = [0.3, 0.4, 0.5, 0.1, 0.15]，标签从大到小排序，0.5-》0.4-》0.3，排到第三个，把标签为1的全部覆盖了，则样本1的覆盖率为（3-1） = 2
样本2，真实标签集y_true = [1, 0, 1, 0, 1]，标签预测概率值y_score = [0.4, 0.5, 0.7, 0.2, 0.6]，标签从大到小排序，0.7-》0.6-》0.5-》0.4，排到第四个，把标签为1的全部覆盖了，则样本1的覆盖率为（4-1） = 3
总的覆盖率为 （2+3）/ 2 = 2.5
程序：

def Coverage(label, logit):
    D = len(label[0])
    N = len(label)
    label_index = []
    for i in range(N):
        index = np.where(label[i] == 1)[0]
        label_index.append(index)
    cover = 0
    for i in range(N):
        # 从大到小排序
        index = np.argsort(-logit[i]).tolist()
        tmp = 0
        for item in label_index[i]:
            tmp = max(tmp, index.index(item)) 
        cover += tmp
    coverage = cover * 1.0 / N
    return coverage
label = np.array([[1, 0, 1, 0, 0], [1, 0, 1, 0, 1]])
logit = np.array([[0.3, 0.4, 0.5, 0.1, 0.15], [0.4, 0.5, 0.7, 0.2, 0.6]])
print(Coverage(label, logit))

结果：

这里注意下，sklearn库里自带了一个方法，

label = np.array([[1, 0, 1, 0, 0], [1, 0, 1, 0, 1]])
logit = np.array([[0.3, 0.4, 0.5, 0.1, 0.15], [0.4, 0.5, 0.7, 0.2, 0.6]])
print(metrics.coverage_error(label, logit))
print(Coverage(label, logit))

这个coverage方法没有在每个样本排序的时候减去1，导致最终结果如下：

本文的程序代码来自多标签评价指标python代码

如有错误，烦请指正。