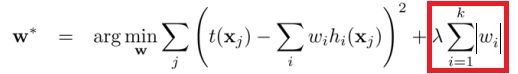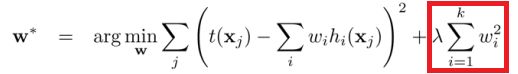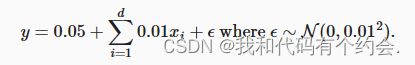Pytorch 权重衰减

目录

1、权重衰减

2、L2正则化和L1正则化

3、高维线性回归演示权重衰减

---

1、权重衰减

一般来说，我们总是可以通过去收集更多的训练数据来缓解过拟合。 但这可能成本很高，耗时颇多，或者完全超出我们的控制，因而在短期内不可能做到。所以我们需要将重点放在正则化技术上，权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为L2正则化

2、L2正则化和L1正则化

L2正则化线性模型构成经典的岭回归（ridge regression）算法， L1正则化线性回归是统计学中类似的基本模型， 通常被称为套索回归（lasso regression）。 使用L2范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中，这可能使它们对单个变量中的观测误差更为稳定。 相比之下，L1惩罚会导致模型将权重集中在一小部分特征上， 而将其他权重清除为零。 这称为特征选择（feature selection），这可能是其他场景下需要的。

L1正则化

L2正则化

3、高维线性回归演示权重衰减

导入所需库

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

定义拟合公式

为了使过拟合效果更加明显，将问题的维数增加到d=200，并只使用包含20个小样本的训练集训练

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

初始化模型参数

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

定义L2范数

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

定义训练代码

def train(lambd):
    w, b = init_params() # 初始化权重
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss #定义Lambda函数
    num_epochs, lr = 100, 0.003 #定义训练论述和学习率
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test']) #定义动画
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
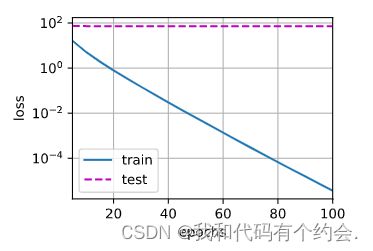
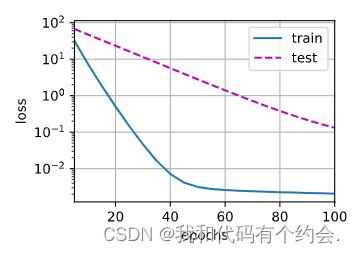
    print('w的L2范数是：', torch.norm(w).item())

设置lambd=0进行训练，显然发生过拟合（测试损失不变，训练损失下降）

train(lambd=0)

 使用权重衰减，即设置lambd=3，训练误差增大了，但测试误差减小，正则化起到效果。

train(lambd=3)