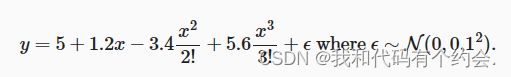Pytorch 多项式拟合
目录
1、训练误差和泛化误差
2、独立同分布假设
3、欠拟合和过拟合
4、多项式回归
1、训练误差和泛化误差
训练误差(training error)是指, 模型在训练数据集上计算得到的误差。 泛化误差(generalization error)是指, 模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望。
一般来说泛化误差无法进行准确计算,实际上我们只能通过将模型应用于一个独立测试集来估计泛化误差,该测试集由随机选取的、未曾在训练集中出现的数据样本构成。
2、独立同分布假设
在深度学习应用过程中,我们假设训练数据和测试数据都是从相同的分布中独立提取的。这通常被称为独立同分布假设,这意味着对数据采样过程中没有进行记忆,也就是说,抽取第2个样本和第3个样本的相关性,并不比抽取第2个样本和第200万个样本的相关性强。
3、欠拟合和过拟合
训练误差和验证误差都很严重, 但它们之间仅有一点差距。 如果模型不能降低训练误差,这可能意味着模型过于简单(即表达能力不足), 无法捕获试图学习的模式。 此外,由于我们的训练和验证误差之间的泛化误差很小, 我们有理由相信可以用一个更复杂的模型降低训练误差。 这种现象被称为欠拟合(underfitting)。
当我们的训练误差明显低于验证误差时要小心, 这表明严重的过拟合(overfitting)
值得注意的是,过拟合并不总是一件坏事。特别是在深度学习领域,最好的预测模型在训练数据上的表现往往比在验证数据上好得多。最终我们更关心验证误差,而不是训练误差和验证误差之间的差距。
4、多项式回归
我们使用多项式回归来验证上述概念
导入所需的库
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l使用下述三阶多项式来生成训练和测试数据的标签:
噪声项∈服从均值为0且标准差为0.1的正态分布。 在优化的过程中,我们通常希望避免非常大的梯度值或损失值。 我们将为训练集和测试集各生成100个样本。
max_degree = 20 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练和测试数据集大小
true_w = np.zeros(max_degree) # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6]) #多项式的前几项
features = np.random.normal(size=(n_train + n_test, 1)) # x (200,1)
np.random.shuffle(features)# 打乱x
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1)) #分别求x的0-19次方
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1) # gamma(n)=(n-1)! 伽玛函数
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w) # 进行乘法,每一行都是一个数据
labels += np.random.normal(scale=0.1, size=labels.shape) #加上噪声项将ndarray转换为tensor
# NumPy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=torch.float32) for x in [true_w, features, poly_features, labels]]
features[:2], poly_features[:2, :], labels[:2]自定义函数评估模型在给定数据集上的损失
def evaluate_loss(net, data_iter, loss): #@save
"""评估给定数据集上模型的损失"""
metric = d2l.Accumulator(2) # 损失的总和,样本数量
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]定义模型训练函数
def train(train_features, test_features, train_labels, test_labels,num_epochs=400):
loss = nn.MSELoss() # 均方误差损失函数
input_shape = train_features.shape[-1]
# 不设置偏置,因为我们已经在多项式中实现了它 第一项 5
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False)) #一个线性层
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
xlim=[1, num_epochs], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
evaluate_loss(net, test_iter, loss)))
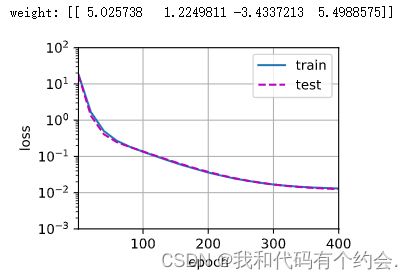
print('weight:', net[0].weight.data.numpy())①正常情况
使用四个参数去拟合三阶多项式, 结果表明,该模型能有效降低训练损失和测试损失。 学习到的模型参数也接近真实值w=[5,1.2,−3.4,5.6]。
# 从多项式特征中选择前4个维度,即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],labels[:n_train], labels[n_train:])②欠拟合
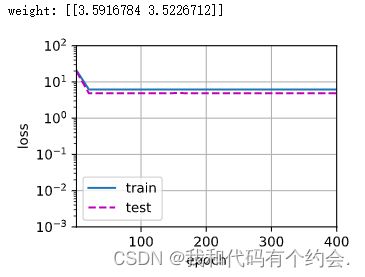
使用两个参数去拟合三阶多项式
# 从多项式特征中选择前2个维度,即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],labels[:n_train], labels[n_train:])经历过多轮迭代损失函数仍然很高,且结果并不好,模型欠拟合。
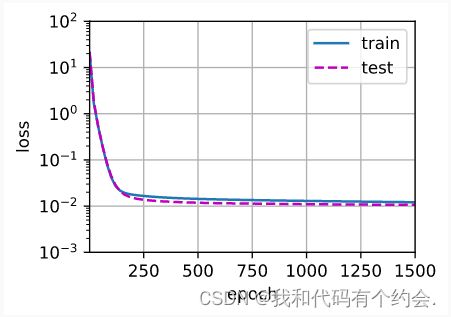
③过拟合
使用全部参数去拟合三阶多项式,虽然训练损失可以有效地降低,但测试损失仍然很高。 结果表明,复杂模型对数据造成了过拟合。
# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:], num_epochs=3000)