理论推导
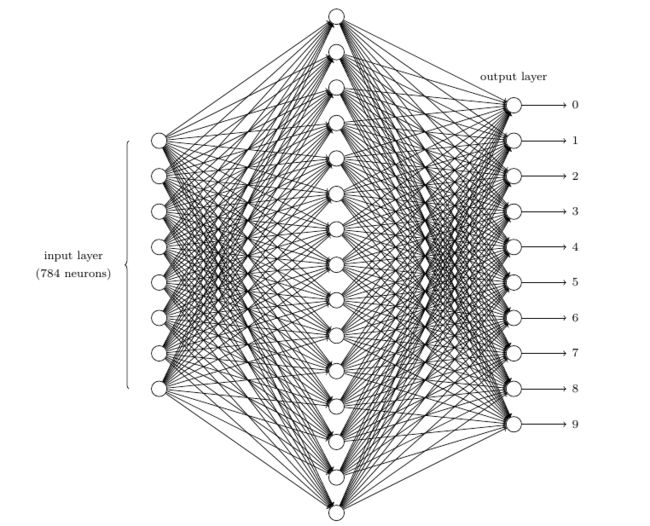
神经网络通常第一层称为输入层,最后一层 \(L\) 被称为输出层,其他层 \(l\) 称为隐含层 \((1
设输入向量为:
\(x = (x_1,x_2,...,x_i,...,x_m),\quad i = 1,2,...,m\)
输出向量为:
\(y = (y_1, y_2,...,y_k,...,y_n),\quad k = 1,2,...,n\)
第\(l\)隐含层的输出为:
\(h^{(l)} = (h^{(l)}_1,h^{(l)}_2,...,h^{(l)}_i,...,h^{(l)}_{s_l}), \quad i = 1,2,...,s_l\)
其中:$ s_l $ 为第 \(l\) 层神经元的个数。
设$ W_{ij}^{(l)} $为第 \(l\) 层的神经元 \(i\) 与第 \(l-1\) 层神经元 \(j\) 的连接权值;$ b_i^{(l)} $为第 \(l\) 层神经元 \(i\) 的偏置,有:
\(h_i^{(l)} = f(net_i^{(l)})\)
\(net_i^{(l)} = \sum_{j=1}^{s_l - 1} W_{ij}^{(l)}h_j^{(l-1)} + b_i^{(l)}\)
其中,$ net_i^{(l)} $是第 \(l\) 层的第 \(i\) 个神经元的输入,\(f(x)\) 为神经元的激活函数:
\(f(x) = \frac{1}{1+e^{-x}} \quad f'(x) = f(x)(1-f(x))\)
算法推导-法一
设 \(m\) 个训练样本:\(\{(x(1),y(1)), (x(2),y(2)), (x(3), y(3)), ... ,(x(m), y(m))\}\) 期望
输出:\(d(i)\)
误差函数:
\[ E=\frac{1}{m}\sum_{i=1}^{m}E(i) \]
$ E(i) $是一个样本的训练误差:
\[ E(i) = \frac{1}{2}\sum^n_{k=1}(d_k(i) - y_k(i))^2\\ y_k(i) = h^{(L)}_k(i) \]
代入有:
\[ E(i) = \frac{1}{2m}\sum_{i=1}^{m}\sum^n_{k=1}(d_k(i) - y_k(i))^2 \]
权值更新:
\[ W_{ij}^{(l)} = W_{ij}^{(l)} - \alpha \frac{\partial E}{\partial W_{ij}^{(l)}} \]
偏置更新:
\[ b_{i}^{(l)} = b_{i}^{(l)} - \alpha \frac{\partial E}{\partial b_{i}^{(l)}} \]
其中:$ \alpha $ 是学习率。
对于单个样本,输出层的权值偏导为:
\[ \frac{\partial E(i)}{\partial W_{kj}^{(L)} } = \frac{\partial}{\partial W_{kj}^{(L)}}(\frac{1}{2}\sum^n_{k=1}(d_k(i) - y_k(i))^2)\\ = \frac{\partial}{\partial W_{kj}^{(L)}}(\frac{1}{2}(d_k(i) - y_k(i))^2)\\ = -(d_k(i) - y_k(i))\frac{\partial y_k(i)}{\partial W_{kj}^{(L)}}\\ = -(d_k(i) - y_k(i))\frac{\partial y_k(i)}{\partial net_k^{(L)}}\frac{\partial net_k^{(L)}}{\partial W_{kj}^{(L)}}\\ = -(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}}\frac{\partial net_k^{(L)}}{\partial W_{kj}^{(L)}}\\ = -(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}}h_j^{(L-1)}\\ \]
则:
\[ \frac{\partial E(i)}{\partial W_{kj}^{(L)} } =-(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}}h_j^{(L-1)} \]
同理有:
\[ \frac{\partial E(i)}{\partial b_k^{(L)} } =-(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}} \]
令:
\[ \delta_k^{(L)} = \frac{\partial E(i)}{\partial b_k^{(L)} } \]
则有:
\[ \frac{\partial E(i)}{\partial W_{kj}^{(L)} } = \delta_k^{(L)}h_j^{(L-1)} \]
对于隐含层 \(L-1\):
\[ \frac{\partial E(i)}{\partial W_{ji}^{(L-1)}} = \frac{\partial}{\partial W_{ji}^{(L-1)}}(\frac{1}{2}\sum_{k=1}^{n} (d_k(i) - y_k(i) )^2 )\\ = \frac{\partial}{\partial W_{ji}^{(L-1)}}(\frac{1}{2}\sum_{k=1}^{n} (d_k(i) - f(\sum_{j=1}^{s_{L-1} } W_{kj}^{(L)} h_j^{(L-1)} + b_k^{(L)} ))^2 )\\ = \frac{\partial}{\partial W_{ji}^{(L-1)}}(\frac{1}{2}\sum_{k=1}^{n} (d_k(i) - f(\sum_{j=1}^{s_{L-1} } W_{kj}^{(L)} f(\sum_{i=1}^{s_{L-2} } W_{ji}^{(L-1)} h_i^{(L-2)} + b_j^{(L-1)}) + b_k^{(L)} ))^2 )\\ = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}}\frac{\partial net_k^{(L)}}{\partial W_{ji}^{(L-1)} }\\ \]
其中:
\[ net_k^{(L)} = \sum_{j=1}^{s_{L-1}} W_{kj}^{(L)}h_j^{(L-1)} + b_k^{(L)}\\ = \sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} f(net_j^{(L-1)}) + b_k^{(L)}\\ = \sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} f(\sum^{s_{L-2}}_{i=1} W_{ji}^{(L-1)} h_i^{(L-2)} + b_j^{(L-1)} )+ b_k^{(L)}\\ \]
代入有:
\[ \frac{\partial E(i)}{\partial W_{ji}^{(L-1)}} = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}}\frac{\partial net_k^{(L)}}{\partial W_{ji}^{(L-1)} }\\ = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}} \frac{\partial net_k^{(L)} }{\partial f(net_j^{(L-1)})} \frac{\partial f(net_j^{(L-1)})}{\partial net_j^{(L-1)}} \frac{\partial net_j^{(L-1)}}{\partial W_{ji}^{L-1} }\\ = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}} W_{kj}^{(L)} f'(x)|_{x=net_j^{(L-1)}} h_i^{(L-2)} \\ \]
同理可得:
\[ \frac{\partial E(i)}{\partial b_j^{(L-1)}} = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}} W_{kj}^{(L)} f'(x)|_{x=net_j^{(L-1)}} \\ \]
令:
\[ \delta_j^{(L-1)} = \frac{\partial E(i)}{\partial b_j^{(L-1)}} \]
有:
\[ \delta_j^{(L-1)} = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}} W_{kj}^{(L)} f'(x)|_{x=net_j^{(L-1)}} \\ = \sum^n_{k=1}\delta_k^{(L)} W_{kj}^{(L)} f'(x)|_{x=net_j^{(L-1)}}\\ \]
\[ \frac{\partial E(i)}{\partial W_{ji}^{(L-1)}} = \delta_j^{(L-1)}h_i^{(L-2)} \]
由此可得,第 \(l(1
\[ \frac{\partial E(i)}{\partial W_{ji}^{(l)}} = \delta_j^{(l)}h_i^{(l-1)}\\ \frac{\partial E(i)}{\partial b_j^{(l)}} = \delta_j^{(l)} \\ \delta_j^{(l)} = \sum_{k=1}^{s_{l+1}} \delta_k^{(l+1)} W_{kj}^{(l+1)}f'(x)|_{x=net_j^{(l)}}\\ \]
算法推导-法二
\[ \frac{\partial E(i)}{\partial W_{kj}^{(L)} } = \frac{\partial E(i)}{\partial h_k^{(L)}} \frac{\partial h_k^{(L)}}{\partial net_k^{(L)}} \frac{\partial net_k^{(L)}}{\partial W_{kj}^{(L)}}\\ = -(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}}h_j^{(L-1)}\\ \]
则:
\[ \frac{\partial E(i)}{\partial W_{kj}^{(L)} } =-(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}}h_j^{(L-1)} \]
对偏置向量求偏导:
\[ \frac{\partial E(i)}{\partial b_k^{(L)} } = \frac{\partial E(i)}{\partial h_k^{(L)}} \frac{\partial h_k^{(L)}}{\partial net_k^{(L)}} \frac{\partial net_k^{(L)}}{\partial b_k^{(L)}}\\ = -(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}}\\ \]
则:
\[ \frac{\partial E(i)}{\partial b_k^{(L)} } =-(d_k(i) - y_k(i))f'(x)|_{x=net_k^{(L)}} \]
令:
\[ \delta_k^{(L)} = \frac{\partial E(i)}{\partial b_k^{(L)} } \]
则有:
\[ \frac{\partial E(i)}{\partial W_{kj}^{(L)} } = \delta_k^{(L)}h_j^{(L-1)} \]
隐含层:
对权值矩阵求偏导:
\[ \frac{\partial E(i)}{\partial W_{ji}^{(L-1)} } = \frac{\partial E(i)}{\partial h_k^{(L)}} \frac{\partial h_k^{(L)}}{\partial net_k^{(L)}} \frac{\partial net_k^{(L)}}{\partial h_j^{(L-1)}} \frac{\partial h_j^{(L-1)}}{\partial net_j^{(L-1)}} \frac{\partial net_j^{(L-1)}}{\partial W_{ji}^{(L-1)}}\\ = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}} W_{kj}^{(L)} f'(x)|_{x=net_j^{(L-1)}} h_i^{(L-2)} \\ \]
对偏置向量求偏导:
\[ \frac{\partial E(i)}{\partial b_j^{(L-1)} } = \frac{\partial E(i)}{\partial h_k^{(L)}} \frac{\partial h_k^{(L)}}{\partial net_k^{(L)}} \frac{\partial net_k^{(L)}}{\partial h_j^{(L-1)}} \frac{\partial h_j^{(L-1)}}{\partial net_j^{(L-1)}} \frac{\partial net_j^{(L-1)}}{\partial b_j^{(L-1)}}\\ = -\sum^n_{k=1}(d_k(i)-y_k(i))f(x)'|_{x=net_k^{(L)}} W_{kj}^{(L)} f'(x)|_{x=net_j^{(L-1)}} \\ \]
推导心得
- 反向传播形象上是从后向前传播,利用后边的信息更新前面的参数。
- 从数学上讲是链式法则,就像链表一样,推导时根据变量的关系,相距较远的参数需要通过中间参数来传递关系。
- 通过将中间关系明确出来,有利于进行数学推导和代码的实现。
- 对带有求和符号求偏导时,关注变量的角标变化,如 $\frac{\partial net_j^{(L)}}{\partial W_{ji}^{L} } $ 中的 $ W_{ji}^{L} $ 的 $ ji $ 是变化的,则求导时就不能对其进行赋值,否则求导就是错误的。
算法实现
BP神经网络的每层结构:
import java.util.Random;
public class Layer {
int inputNodeNum;// 输入维度
int outputNodeNum;// 输出维度
double[] output;// 输出向量
double[][] weights;// 权值矩阵
double[] bias;// 偏置
double[] biasError;// 偏置误差
Layer(int inputNum, int outputNum, double rate){
this.inputNodeNum = inputNum;
this.outputNodeNum = outputNum;
this.rate = rate;
// 初始化向量和矩阵
output = new double[outputNodeNum];
weights = new double[outputNodeNum][inputNodeNum];
bias = new double[outputNodeNum];
biasError = new double[outputNodeNum];
Random r = new Random(2);//固定高斯分布
// 权值和偏置初始化
for (int i = 0; i < outputNodeNum; i++) {
for (int j = 0; j < inputNodeNum; j++) {
weights[i][j] = Math.sqrt(0.09) * r.nextGaussian() - 0.25;
}
bias[i] = 0.0d;
output[i] = 0d;
biasError[i] = 0.0d;
}
}
}正向传播:
// 激活函数
public double actFun(double x){
return 1/(Math.exp(-x)+1);
}
// 隐含层输出
public void hideLayerOutput(Layer h, double[] preLayerOutput){
for (int i = 0; i < h.outputNodeNum; i++) {
double tmp = 0.0d;
for (int j = 0; j < h.inputNodeNum; j++) {
tmp = tmp + h.weights[i][j] * preLayerOutput[j];
}
tmp -= h.bias[i];
h.output[i] = actFun(tmp);//隐含层输出
}
}反向传播:
// 输出层偏置误差
public void outputLayerBiasError(Layer y, double[] target){
if(y.outputNodeNum != target.length){
System.out.println("输出层偏置误差计算维度错误!");
return;
}
for (int i = 0; i < y.outputNodeNum; i++) {
y.biasError[i] = (target[i]-y.output[i])*y.output[i]*(1-y.output[i]);
}
}
// 隐含层偏置误差
public void hideLayerBiasError(Layer h, Layer y){
for (int i = 0; i < h.outputNodeNum; i++) {
double tmp = 0.0d;
for (int j = 0; j < y.outputNodeNum; j++) {
tmp = tmp + y.weights[j][i] * y.biasError[j];
}
h.biasError[i] = tmp * h.output[i]*(1-h.output[i]);
}
}
// 更新输出层的权值和偏置
public void updateOutputWeightBias(Layer h, Layer y){
for (int i = 0; i < y.outputNodeNum; i++) {
for (int j = 0; j < y.inputNodeNum; j++) {
y.weights[i][j] = y.weights[i][j] + y.rate * y.biasError[i] * h.output[j];
}
y.bias[i] += (y.rate * y.biasError[i]);
}
}
// 更新隐含层的权值和偏置
public void updateHideWeightBias(Layer h, double[] inputValue){
if(inputValue.length != h.inputNodeNum){
System.out.println("输入数据与隐含层的输入维度不一致,错误!");
return;
}
for (int i = 0; i < h.outputNodeNum; i++) {
for (int j = 0; j < h.inputNodeNum; j++) {
h.weights[i][j] = h.weights[i][j] + h.rate * h.biasError[i] * inputValue[i];
}
h.bias[i] = h.bias[i] + h.rate * h.biasError[i];
}
}读数据:
// 读数据,将文件数据读入到二维数组中
public void readData(double[][]trainData, double[][] labelData, String pathData, String pathLabel){
File data = new File(pathData);
File label = new File(pathLabel);
BufferedReader da = null;
BufferedReader la = null;
try {
da = new BufferedReader(new FileReader(data));
la = new BufferedReader(new FileReader(label));
}
catch (FileNotFoundException e) {
e.printStackTrace();
}
String line = "";
String labelValue = "";
int count = 0;
try {
while ((line = da.readLine()) != null && (labelValue=la.readLine())!= null) {
// 读取数据并赋值给labelValue
String[] str = line.split("[\\,]+");
for (int i = 0; i < 784; i++) {
trainData[count][i] = Double.parseDouble(str[i])/255;//归一化
//System.out.println(inputValue[count][i]*255); //读数据没问题
}
int inx = Integer.parseInt(labelValue);// 标签值赋值
for (int i = 0; i < 10; i++) {
if(inx != i){
labelData[count][i] = 0;
}
else {
labelData[count][i] = 1;
}
}// 读数据没问题
++count;
}
}
catch (IOException e) {
e.printStackTrace();
}
}单个样本误差计算:
// 计算样本误差值
public double sampleError(double[]target, double[] output){
double tmp = 0.0d;
for (int i = 0; i < target.length; i++) {
tmp = tmp + (target[i]-output[i])*(target[i]-output[i]);
}
return tmp / 2.0;
}将数据导入网络训练:
// 将数据导入网络并进行训练
public void dataToNet(double[]inputValue, Layer h,Layer y,
double[][]trainData, double[][] labelData,
double[] target){
Random rad = new Random();
for (int m = 0; m < 3; m++) {
for(int i=30001,count=0; count++<28000;
i=rad.nextInt(30000)%(30000+1)+ 30000){// 随机读取20000条数据训练
for (int j=0, r=0; j < trainData[i].length; j++) {
inputValue[j] = trainData[i][j];// 输入向量赋值
}
for (int k = 0; k < labelData[i].length; k++) {
target[k] = labelData[i][k];// 标签赋值
}
// 训练,此处发现每增加一次,准确就增加一点
for (int j = 0; j < 3; j++) {//每个样本训练100次
train(h,y,inputValue,target);
double er = sampleError(target, y.output);//输出样本误差大小
System.out.println(er);
}
}
}
}检查是否预测正确:
// 预测单个样本的正确与否
public int predictSingleSample(Layer s, double[] target){
double rightRate = 0;// 正确率
double max = -1.0d,index = -1;
for (int i = 0; i < s.output.length; i++) {
if(s.output[i] > max) {// 找到softmax输出的最大概率,视为预测值
max = s.output[i];
index = i;
}
}
for (int i = 0; i < target.length; i++) {
// 预测值和实际值比对
if(target[i] > 0) {
if (i == index)
return 1;// 预测正确
}
}
return 0;// 预测错误
}读取10000个数据进行预测:
//导入测试集数据并预测所有样本的正确率,测试集大小10000
publicvoidpredict(double[][]predictData,double[][]predictLabel,
Layerh,Layery,double[]inputValue,double[]target){
doublerightRate=0.0d;
Randomrad=newRandom();
intcount=0;
for(inti=0;count++<10000;
i=rad.nextInt(30000)%(30000+1)){
for(intj=0;j