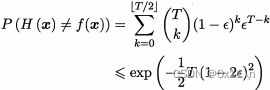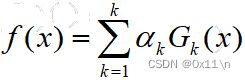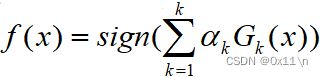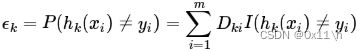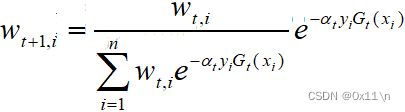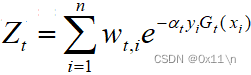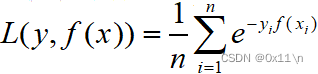集成学习 adaBoost

adaBoost

1.集成学习

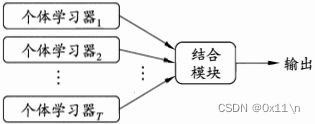
集成多个个体学习器结合起来产生一个组合模型，通常称为“组件学习器”

多学习器组合相对于单一的学习器有显著优越的泛化能力，通常经验来说把好坏的东西掺到一起(即弱学习器和强学习器组合)，得到的结果会介于最好的和最坏的之间。如果集成多个学习器如何能获得比最好的单一学习器更好的性能呢？我们以多数服从少数来计算最终结果：

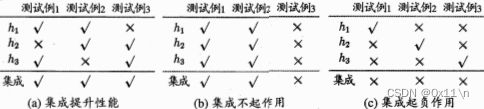
可以看到，要获得好的集成。个体学习器应该“好而不同”，即个体学习器需要有一定的准确性不能太坏且学习器之间要有多样性。

考虑二分类器y∈{-1,+1}和函数f，假设基本分类器的错误率为ε，f(x)为真实结果，h(x)为分类结果，则错误率为

基分类器h(x)有一定分类准确性，如果误差相互独立，即分类器有完全的多样性，那么超过半数分类正确则集成分类正确，集成分类器为

那么集成错误率会随着基分类器的个数增大而指数级降低，最终趋于零

但是一般的个体学习器之前不可能有完全多样性，因为大家都是为解决同一个问题而训练的显然其误差肯定存在某种相关性而不可能相互独立。

根据个体学习器的生成方式可以分为两大类，第一种个体学习器之间存在强依赖关系，必须串行生成的方法(boosting为代表)，第二种是个体学习器之间不存在强依赖关系可并行同时生成的方法(随机森林为代表)。

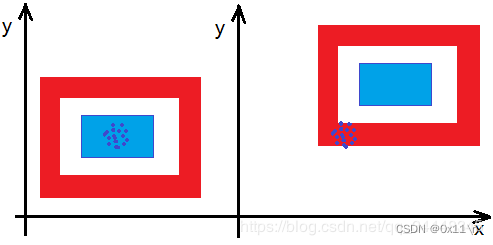
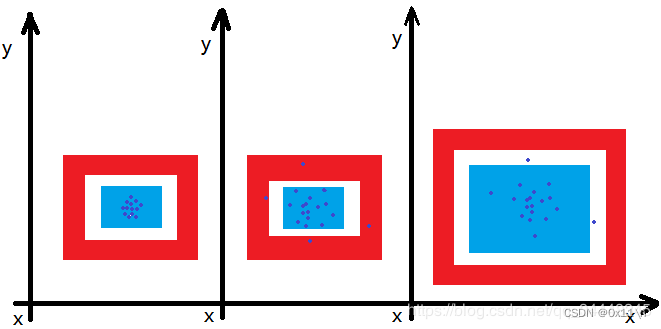
通常泛化误差含两个部分，以下图蓝点颜色预测为例

偏差：度量模型预测值和期望值的偏离程度，偏差越大即预测值越偏离真实值，刻画了模型本身的拟合能力。低偏差，可能因为对目标函数提出更少的假设。高偏差，可能因为对目标函数提出更多的假设。

方差：度量训练数据的变化造成学习到的模型变化程度，刻画了数据扰动对模型性能造成的影响。低方差，随着训练数据集的变化，对目标函数估计值的变化非常小。高方差，随着训练数据集的变化，对目标函数估计值的变化非常大。

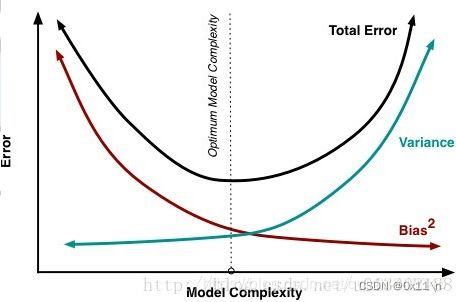
模型复杂度和误差的关系变化

通常我们想要找到交点(即方差和偏差均很小)时的模型，通常

如果模型高偏差：

可以增加特征种类、增加多项式次数、降低正则化项系数

如果模型高方差：

可以增加数据集、去掉一部分特征、增加正则化项系数

而集成学习boosting中是降低偏差为主，而bagging是降低方差为主。

2.boosting

这一类算法是可将弱学习器提升为强学习器的算法，工作机制为：先从初始训练集D1训练出一个基学习器，再根据基学习器的表现对训练样本的分布进行调整得到D2，使得先前得到的基学习器错误率增大(使那些被错误分类的样本得到更多的关注)。再根据D2得到下一个学习器，如此重复。直到基学习器的个数达到指定T个，将这T个基学习器加权结合得到一个组合学习器。

3.adaboost

工作流程是，拿出前一个分类器分类错误的那些样本，让这些被分类错误的样本在样本整体中的权值增加，得到修改后的样本整体再去训练下一个分类器，这是一次完整的迭代。每次迭代都得到新的样本整体和新的基分类器，直到迭代达到指定次数或者当前基分类器的错误率达到指定标准。

以二分类为例做推导：

设样本为T，二分类结果为y∈{-1,+1}，如下

初始样本权重D(1)，每个样本占相同的比重如下

使用带权值的样本(T*D)进行训练得到分类器G。迭代到第k次的分类器如下

得到最终的集成分类器是前面k个分类器的组合，如下

对于二分类问题，用sign函数将线性转为二值，如下

其中分类器系数为α，代表的是每个分类器的权重，显然要让分类误差小的基分类器在集成分类器中比重更大。而按照迭代过程，被错误分类的样本的权重D之和越小则分类误差越小，则分类误差如下

首先如果一半以上样本都判错的基分类器不符合基分类器的“一定准确性”条件。所以需要找到α和ε的一组关系，存在当ε<1/2时，α>0且随着ε减小而增大。则分类器系数可以取

最后只剩下具体的样本权重更新式就可以整个过程串联。通过D(t)计算D(t+1)公式如下

其中分母部分Z叫做规范化因子，作用是将D(t+1)变成一个概率分布，如下

所以adaboost串行计算生成最后的基分类器的影响传递为

4.指数损失函数

样本权重更新式的推导来自于损失函数最小化，类似于逻辑回归相关的对数损失函数、平方损失函数(最小二乘)等等，adaboost使用指数损失函数，对于n个样本如果有真实值y和预测值f(x)，则函数f的指数损失如下