MATLAB递推最小二乘法（三输入一输出ARX模型、所有样本数据权重为1）

假设：读者已经掌握了矩阵的基本运算、ARX模型结构、最基本的最小二乘法、MATLAB 编程语言

一、主要参考书籍

二、主要参考公式

三、ARX模型结构、以及最小二乘法回顾

四、MATLAB代码

%% 递推最小二乘法，是广义预测控制的基础之一

%% 程序版本迭代记录
%%%% 2022.10.2 最普通的RLS A_RLS.m
%%%% 2022.10.5 最普通的RLS,初始的三个矩阵通过小批量的历史数据利用一次性最小二乘法先得到 A_RLS_2.m

%% 清除
clc;clear;close all;

%% 导入数据
% all_data = readmatrix('F:\E\data_needed.xlsx','Sheet',4,'Range','B1000:H17001'); % 这是原始状态值
% all_data = readmatrix('F:\E\data_needed.xlsx','Sheet',4,'Range','I1000:O17001'); % 这是剔除异常值后状态值
all_data = readmatrix('F:\E\data_needed.xlsx','Sheet',4,'Range','P1000:V42001'); % 这是滤波后状态值
% all_data = readmatrix('F:\E\data_needed.xlsx','Sheet',4,'Range','W10000:AC42001'); % 这是增量值

%% 利用采样周期调整步长
sample_cycle = 30; % 采样周期 30s
sample_cycle_number = 2; % 2个采样周期为一个步长
predict_cycle = sample_cycle_number * sample_cycle; % 预测周期是sample_cycle_number个30s 

%% 估计时延
delay_feed = sample_cycle * 20; % 600s
delay_coal = sample_cycle * 20; % 600s
delay_fan = sample_cycle * 12; % 360s

delay_feed = delay_feed / predict_cycle; % 换算为步长
delay_coal = delay_coal / predict_cycle; % 换算为步长
delay_fan = delay_fan / predict_cycle; % 换算为步长

%% 各变量观测值数据的起点、终点
data_start = 2000; 
data_end = data_start + 10000; 

%% 按照变量分割数据（预测周期变了）
u_feed=all_data(data_start : sample_cycle_number : data_end, 1);
u_coal=all_data(data_start : sample_cycle_number : data_end, 2);
u_fan=all_data(data_start : sample_cycle_number : data_end, 3);
y_temp=all_data(data_start : sample_cycle_number : data_end, 7);

%% 数据样本数
N = size(y_temp, 1);

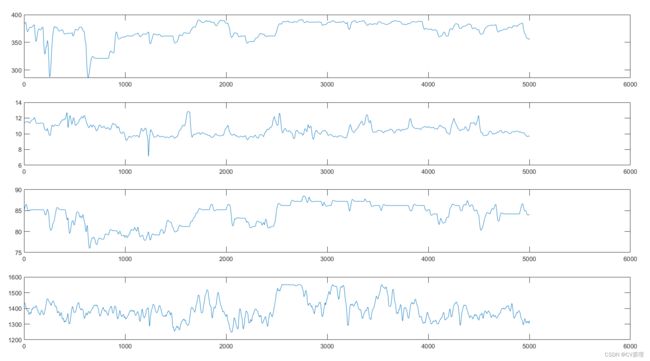
%% 数据可视化
figure('Name','数据可视化','NumberTitle','off');
subplot(411);
plot(u_feed);
subplot(412);
plot(u_coal);
subplot(413);
plot(u_fan);
subplot(414);
plot(y_temp);

%% 给输出添加测量噪声
noise_intensuty = 0.05;
rng('default');
y_temp = y_temp+noise_intensuty * normrnd(0,1,N,1); % N行1列的随机数矩阵

%% 递推最小二乘法，部分参数值需要初始化（其实应该先用少量实际的样本数据，利用一次性最小二乘法，求得ps_old、P_old）
n = 1000; % 用1000个样本辨识ARX模型参数矩阵的初始值
Y = y_temp(100 : 100 + n, :); % 构造Y矩阵
H = [y_temp(100 - 1 : 100 + n - 1, :) ...
     y_temp(100 - 2 : 100 + n - 2, :) ... 
     u_feed(100 - delay_feed - 1 : 100 + n - delay_feed - 1, :) ...
     u_feed(100 - delay_feed - 2 : 100 + n - delay_feed - 2, :) ...
     u_coal(100 - delay_coal - 1 : 100 + n - delay_coal - 1, :) ...
     u_coal(100 - delay_coal - 2 : 100 + n - delay_coal - 2, :) ...
     u_fan(100 - delay_fan - 1 : 100 + n - delay_fan - 1, :) ...
     u_fan(100 - delay_fan - 2 : 100 + n - delay_fan - 2, :)]; % 构造H矩阵

P_old = inv(H' * H); % P矩阵初始值
ps_old = P_old * H' * Y; % ARX模型参数矩阵初始值
MRE_target = 0.000000000001; % 辨识所得参数的相对误差的目标值
ps_history = [ps_old]; % 方便后面记录ARX模型参数的每一轮递推更新后的值

%% 正式开始执行递推最小二乘辨识算法
for k = 1000 : 1 : N
    %%%% 构造一行新的h矩阵
    h_new = [y_temp(k-1, :) y_temp(k-2, :) ...
             u_feed(k - delay_feed - 1, :) u_feed(k - delay_feed - 2, :) ...
             u_coal(k - delay_coal - 1, :) u_coal(k - delay_coal - 2, :) ...
             u_fan(k - delay_fan - 1, :) u_fan(k - delay_fan - 2, :)];
    %%%% 计算新的增益矩阵K
    K_new = P_old * h_new' * inv(1 + h_new * P_old * h_new');
    %%%% 计算新的模型参数矩阵
    ps_new = ps_old + K_new * ( y_temp(k, :) - h_new *  ps_old );
    %%%% 计算新的矩阵逆P
    P_new = P_old - P_old * h_new' * inv( 1 + h_new * P_old * h_new') * h_new * P_old;
    
    MRE = max(abs((ps_new - ps_old) ./ ps_old )); % 计算新的模型参数矩阵里各参数相对误差里最大的那个
    
    if MRE <= MRE_target 
        break; % 若参数收敛满足要求，终止辨识
    end
    %%%% 把新的P、ps作为下一轮循环的初始值
    P_old = P_new;
    ps_old = ps_new;
    
    %%%% 记录历史的ARX模型参数值
    ps_history = [ps_history ps_old];
end

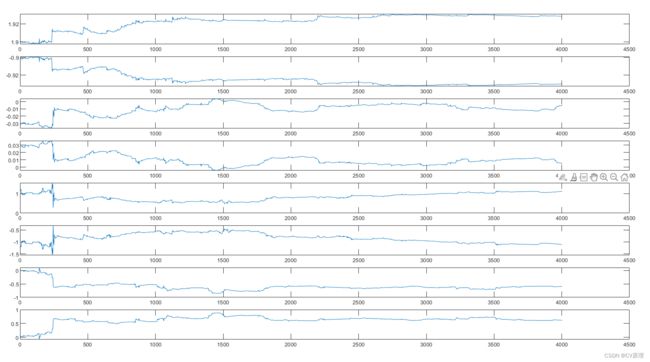
%% ARX模型参数值递推变化
figure('Name','ARX模型参数值递推变化','NumberTitle','off');
subplot(811)
plot(ps_history(1, :));
subplot(812)
plot(ps_history(2, :));
subplot(813)
plot(ps_history(3, :));
subplot(814)
plot(ps_history(4, :));
subplot(815)
plot(ps_history(5, :));
subplot(816)
plot(ps_history(6, :));
subplot(817)
plot(ps_history(7, :));
subplot(818)
plot(ps_history(8, :));

%% 命令窗口调试
N
k
ps_new

五、MATLAB代码运行结果

数据曲线图

ARX模型各个参数每一轮更新后的值

六、注意事项

1.数据不做分享，请理解；
2.MATLAB代码需要读者朋友根据自身需要做出相应的修改，切忌生搬硬套；
3.本文作者水平有限，本文如有错误，请您私信联系。