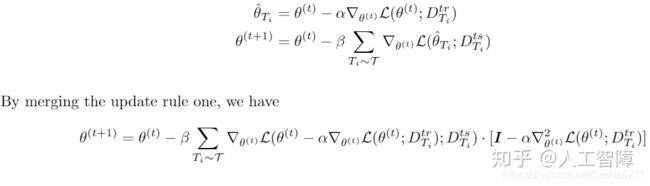MAML代码及理论的深度学习 PyTorch二阶导数计算

PyTorch二阶导数

torch.autograd.grad 函数

x=torch.tensor([2.0],requires_grad=True)
y=x**2

#首先是求一阶导数，显然为2x=4

grad=torch.autograd.grad(y,x,create_graph=True,retain_graph=True) #保存计算图
#y对x求导，x为参数，设置create_graph=True,retain_graph=True保存计算图

print(grad[0]) # 4

f=x-grad[0]  #此处参数为f=x-2*x=-x

print(f)   # -2

y=f*20    #y=20*(-x)

grad2=torch.autograd.grad(y,f) 
#此时y对f求导数，显然为20

grad3=torch.autograd.grad(y,x)
#此时y对x求导数，由于保存了一阶导数的计算图，所以此处为g=-1*20=-20
#如果没有保存一阶导数的计算图，所以此处为g=1*20=20

torch.nn.Conv2和nn.functional.conv2重要区别

在MAML的代码里发现用的是自己定义的权重w和偏置b，然后使用了 F.conv2d(x, w, b, stride=1, padding=0)这种写法，我还奇怪为什么不能用nn.Conv2d，如果是复杂的代码这不是更简单的吗？

然后发现nn.Conv2d这个卷积类它不！能！改！参！数！即使手动改了，后面梯度下降的时候它也会自己把自己改回去，所以就只能一个一个参数的写了？？？好大的工程量呀，偷懒失败！

MAML原理的深度理解

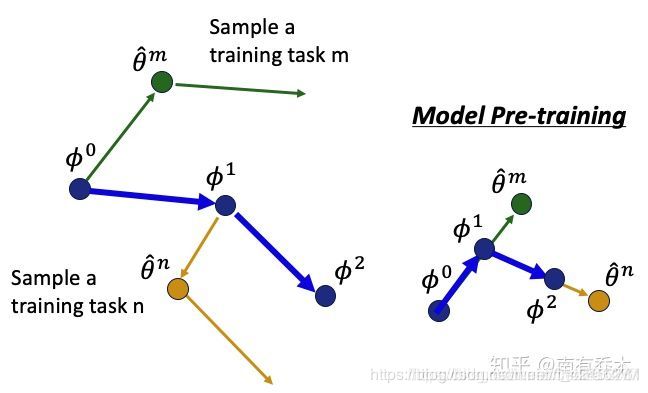
一直都不能理解MAML的原理，看了知乎大神们的分析，终于有一点了解了。MAML算法，model-agnostic metalearnings

MAML学习的就是初始化参数的规则。这个初始化的参数θ在参数空间中具有对每个任务最优参数解θ1,2,…n的高度敏感(其实就是梯度方向垂直)，使其能够在一步Gradient Descent中沿着梯度方向快速达到最优点。

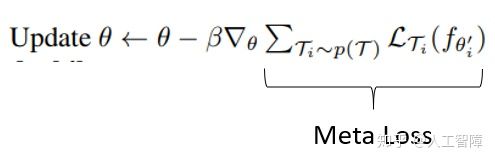
θ’是θ在support set上梯度下降的一步之后的结果，我们用这个θ‘在query set上计算损失，但是是对θ求导，而不是对θ’求导，就等与在这个过程中引入了θ的二阶导数信息。

可以看到整个过程梯度的下降有后面的一个二阶导数的小尾巴。

但是呢，MAML对这个二阶导的计算做了近似，因为不近似的话二阶导要保存计算图，存储空降和计算速度都会受到影响，很是复杂。


这个近似就是把二阶导数置为0了（？？？）这么粗暴的吗？这样在第二步梯度下降中，看似好像是L(θ‘)对θ在求导，但其实呢，L(θ‘)还是在对θ‘在求导

所以这个时候的MAML代码就是没有保存计算图的版本。

for i in range(task_num):

    # 1. run the i-th task and compute loss for k=0
    logits = self.net(x_spt[i], vars=None, bn_training=True)
    loss = F.cross_entropy(logits, y_spt[i])
    #可以看到下面的这个grad的计算图没有保存
 	grad = torch.autograd.grad(loss, self.net.parameters())
 	fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, self.net.parameters())))
 	for k in range(1, self.update_step): #第二步更新了
 		logits = self.net(x_spt[i], fast_weights, bn_training=True)
 		loss = F.cross_entropy(logits, y_spt[i])
 		grad = torch.autograd.grad(loss, fast_weights) 
 		#这里就不用对net的参数求导，近似为对fastw求导
 		fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, fast_weights)))
 		logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
        # loss_q will be overwritten and just keep the loss_q on last update step.
        loss_q = F.cross_entropy(logits_q, y_qry[i])
        losses_q[k + 1] += loss_q
    self.meta_optim.zero_grad()
    loss_q.backward()
    self.meta_optim.step()
    #这里的loss是对net的参数求导，虽然里面有fastw，但由于没有保存计算图，所以其对net的导数为1

如果需要引入二阶导（实验证明这样会有很大的提升），可以把第一步的计算图保存。

grad = torch.autograd.grad(loss, self.net.parameters(),create_graph=True,retain_graph=True)

但是只需要保存第一步梯度下降就可以啦。我还傻乎乎的把第二次的梯度下降的fastw改为net的参数又保存了一次计算图，这样就是求了三阶导数？

实践证明这样的效果应该是最好的。

总而言之，最终的效果大概就是这样。

这个问题的本质就是不断在参数空间中寻找一个位置（这个位置不对应任何任务的最优解）最终收敛，但是这个位置却神奇地对应着很多任务最优解的最近处。用这个位置给模型进行初始化以后，具备朝任何一个给定的task最优参数的位置快速前进(只优化一步)的能力（来自知乎）。

这个图我很喜欢

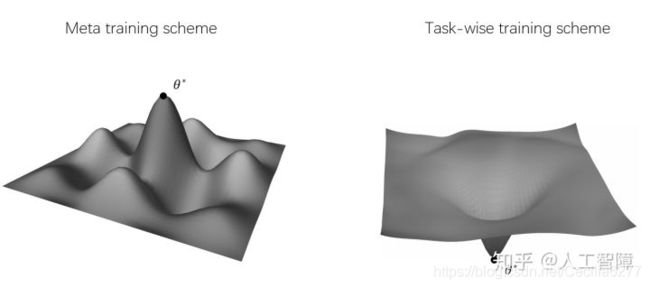
方案1 更可能分布在一个peak上，被每个task最优解围绕，容易收敛到最优解。 方案2 更像右图，试图找到一个单一解对所有task的泛化性能最好。

那么问题来了，该怎么把MAML应用到目标检测上去呢？