关于梯度下降与Momentum通俗易懂的解释

sgd与momentum都是常见的梯度优化方法。本文想从代码方面对这两种方法进行总结。

关于理论。建议参考:
https://www.cnblogs.com/jungel24/p/5682612.html
这篇博文写的很好。很形象。本文也是建立在它的基础上写的，同时代码参考：
https://github.com/hsmyy/zhihuzhuanlan
?。交代完毕，开始学习之旅。
之前在学习无论是ML，DL的时候，总是理论优先，很多都是知道是那么回事，但是从没想过如何用代码实现。随着学习的深入，越来越觉得越是基础的东西，越要注意。所以这篇博客就是我的一个学习方法的改进，本文会在上面代码的基础上代码总结。

我写的和原链接不同。手法方面没有那么好看，但是更容易理解，特别是momentum部分，很不一样，很适合初学者，因为没有太多的包装。也是因为我没有养成好的coding习惯导致的。。。但是正确性是可以保证的，我都亲自运行过。

1.gd

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-5,7,500)
y = (x-1)**2
#g(x)为导数
def g(x):
    return 2*x-2
plt.plot(x,y)

def gradient_descent(x0,step,epoch):
    x = x0
    for i in range(epoch):
        print('epoch:{},x= {},gradient={}'.format(i,x,g(x)))
        x-=step*g(x)
        if abs(g(x))<=1e-6:#注意这里别忘了取绝对值了，我一开始就忘了。
            return x
    return x

主体构建完毕。接下来：

gradient_descent(4,0.1,20)

初始点选为4，学习率为。0.1，迭代20次:

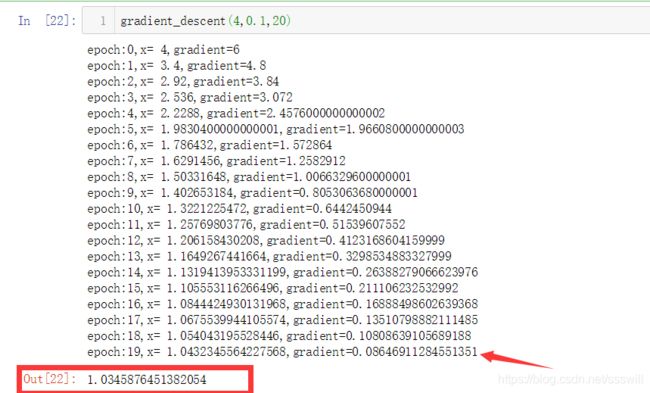
可以看到，最后已经十分接近于解析解1了，同时梯度也很接近于0.很棒。
倘若我们把学习率加大呢？

gradient_descent(4,5,20)

可以看到是越来越偏的。

2.momentum

为了更好的看出来sgd的问题所在，与momentum的强大之处：我们这次采用二元函数：
z=x**2 + 50*y**2。我们现在就可以假设loss function为上面的函数，x,y则为自变量，想用梯度下降法找到最优解。显然这个函数在（0，0）处有最优解，那么来看看梯度下降如何处理：
先来看看图象长什么样:

import numpy as np
import pylab as plt

f(x)就是上面的函数，

def f(x):
    x = np.array(x)
    return x[0]**2+50*x[1]**2
def g(x):
    x = np.array(x)
    tidu = np.array([2*x[0],100*x[1]])
    return tidu
x_plot = np.linspace(-200,200,1000)
y_plot = np.linspace(-100,100,1000)
X,Y = np.meshgrid(x_plot,y_plot)

Z = X**2+50*Y**2
plt.contour(X,Y,Z)
plt.plot(0,0,marker='*')

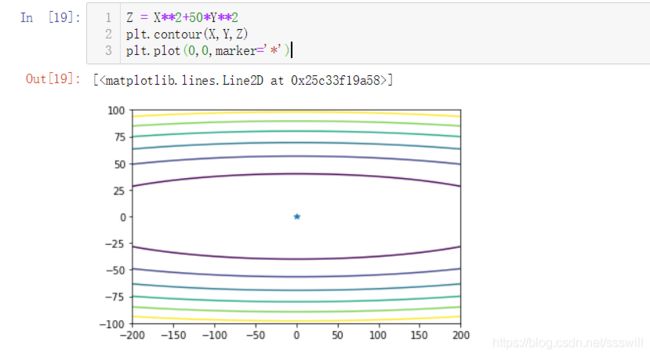
暂停下，上面的知识点:X,Y = np.meshgrid(x_plot,y_plot)
以及plt.contour(X,Y,Z)。
首先说下第二个：contour函数是画等高线图的。第一个meshgrid函数：
https://zhuanlan.zhihu.com/p/29663486
下面截图来自上面这个链接。
Meshgrid函数的一些应用场景
Meshgrid函数常用的场景有等高线绘制及机器学习中SVC超平面的绘制（二维场景下）。
Meshgrid函数的基本用法
在Numpy的官方文章里，meshgrid函数的英文描述也显得文绉绉的，理解起来有些难度。

可以这么理解，meshgrid函数用两个坐标轴上的点在平面上画网格。

用法：

[X,Y]=meshgrid(x,y)

[X,Y]=meshgrid(x)与[X,Y]=meshgrid(x,x)是等同的

[X,Y,Z]=meshgrid(x,y,z)生成三维数组，可用来计算三变量的函数和绘制三维立体图

def gd(x0,step,epoch):
    x = np.array(x0,dtype='float64')
    x_list=[]
    for i in range(epoch):
        x_list.append(x.copy())
        print('epoch:{},x = {},gradient={}'.format(i,x,g(x)))
        x-=step*g(x)
        if abs(sum(g(x)))<=1e-6:
            return x
    return x,x_list

1.x_list.append(x.copy())中的.copy是必须要加的。不加的话x_list都是同一个值。

为了不使得本文太长，关于这个的解释我放到了：
https://blog.csdn.net/ssswill/article/details/86695607

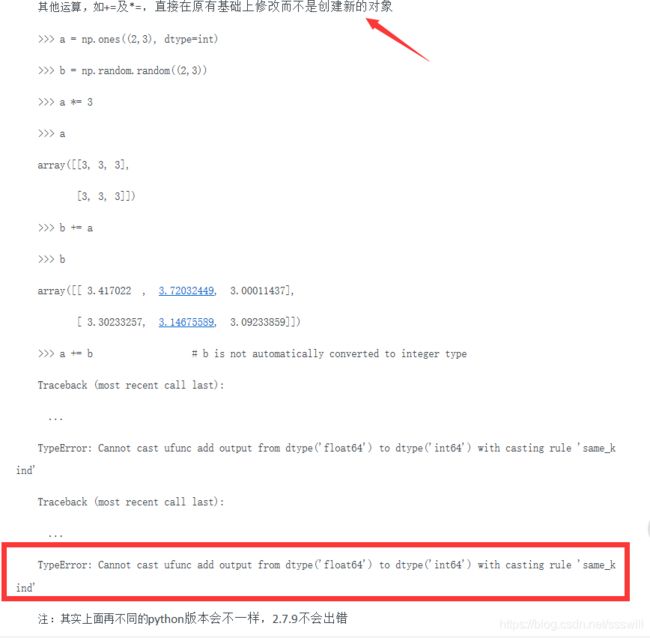
2. x = np.array(x0,dtype=‘float64’)中的floate64是必须加的。（取决于你选的初始点），当然还是建议加的。如不加：

因为原来初始点选的是整数点，为int32类型。之后x-=step*g(x)相当于你还要用int32来存储floate64的结果，显然放不下，报错就是这个意思。
关于这点:http://blog.51cto.com/youerning/1714455

3.关于abs(sum(g(x)))

因为g(x)导数是2个元素组成的向量，所以这里用了求和

4.关于x_list。它存储了每次梯度变化的位置坐标，用来画图的。

go on.

x,x_list = gd([100,75],0.019,50)
plt.figure(figsize=(15,7))
plt.contour(X,Y,Z)
plt.plot(0,0,marker='*')
for i in range(len(x_list)):
    plt.plot([x_list[i][0],x_list[i+1][0]],[x_list[i][1],x_list[i+1][1]])
    if i==48:
        break

我这里选择的初始点是（100，75），学习率为0.019，来看看效果：

可以看到50次之后呢，还是到不了最优点，而且x=14.多，差得远。原因很简单，x方向梯度太小了。如果增大学习率呢？这样不就行了嘛?
我这里把学习率从0.019增加到0.2.来看看:

x,x_list = gd([100,75],0.02,50)
plt.figure(figsize=(15,7))
plt.contour(X,Y,Z)
plt.plot(0,0,marker='*')
for i in range(len(x_list)):
    plt.plot([x_list[i][0],x_list[i+1][0]],[x_list[i][1],x_list[i+1][1]])
    if i==48:
        break

吃惊。变成了这个鬼样子，甚至y方向都不收敛了，而且x也只到了13.多，还是不行。而且看来学习率不能再增大了，0.019是刚好的。那咋办?我就想让它在50次内收敛，难道没办法了嘛?

momentum来了！这是重点，我自己的一些理解:我们呢再来仔细看这个问题，gd不能使用的原因就是x方向梯度太小了，每次在x方向更新速度十分缓慢。反而y方向梯度很大，不到几个回合就到0附近了，甚至还会超过去。我们能不能牺牲一下y的梯度来增强x方向的梯度呢?或者换句话说，你只要能找到一种方法把x方向的梯度增大了，那这事就成了。这样看来，事就好办了。有很多种方法都可以增大x的梯度，momentum就是其中一种。

其实momentum只在gd基础上加了一句话：

        pre_gd = mu*pre_gd+g(x)
        x-=step*pre_gd

我们每次坐标更新变成了这样。梯度由两部分组成：一部分是我们见过的gd的g(x)，也就是该点的导数了。我们刚不是说它太小嘛。那就给他加一点东西咯。所以在这里就加了mupre_gd。mu是一个折扣系数，0.5，0.7，0.9这个样子，它是超参数，由你设置。这里的mupre_gd意思就是上一次梯度的mu倍。这样x的梯度不就增大了吗。同时y方向的梯度是被消弱了的，因为前一次y的梯度总是与这次相反。（其实这句话不对，但是在本例很多限制条件下是没问题的。）
这就达到了x梯度增大，y梯度减小的目的。
再从物理的角度来探讨：momentum就是冲量，动量的意思。先从动能说起，我们想让x方向速度变大，那么y方向速度应该减小。同时对于动量来说，我们这样做相当于不断增大x的动量，而Y方向动量是不断抵消的，大概这个意思吧。

说了那么多，来看看效果吧。

def momentum(x0,step,mu,epoch):
    x = np.array(x0,dtype='float64')
    x_list=[]
    pre_gd = np.array([0,0])
    for i in range(epoch):
        x_list.append(x.copy())
        print('epoch:{},x = {},gradient={}'.format(i,x,g(x)))
        pre_gd = mu*pre_gd+g(x)
        x-=step*pre_gd
        if abs(sum(g(x)))<=1e-6:
            return x
    return x,x_list

x,x_list = momentum([100,75],0.01,0.7,50)
plt.figure(figsize=(15,7))
plt.contour(X,Y,Z)
plt.plot(0,0,marker='*')
for i in range(len(x_list)):
    plt.plot([x_list[i][0],x_list[i+1][0]],[x_list[i][1],x_list[i+1][1]])
    if i==48:
        break

我这里只用了0.01的学习率。

很完美的。这时候为了更清楚看清momentum，我再用0.025的学习率看看如何，代码不贴出来了，和上面一样，只是改了个参数。

我箭头指的地方。是不是就是x的动量很大，y很小的例子。他因为这时候y方向不受力或受力很小，x方向受力较大，所以是这样子。

最后:你如果自己调这些代码时，你可以清楚地发现学习率与mu的重要性，稍微改变一点，图象就会大变。这还仅仅是一个简单的二元函数。在真实应用中，那么多参数，那么复杂的网络，调参可没那么简单。