并查集详解（C/C++）

并查集基础

并查集是什么？

并查集是用来管理元素分组的算法。

并查集的作用是什么？

并查集可以高效的对元素进行分组（合并在一起），并且能快速的查询两个元素是否属于同一组。

并查集的结构

合并

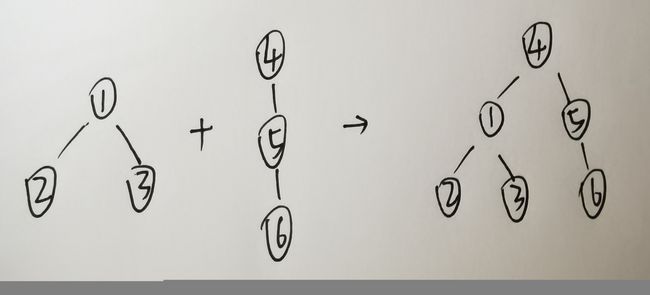
并查集是一种树状结构。比如元素1和2属于同一组、元素1和3也属于同一组，那么元素2和3能通过元素1合并为同一组，即元素1为元素2和3的老大，那么元素1就是元素2和元素3在树状结构中的根。

当许多组元素需要合并在一起时，只需将各组元素的老大合并在一起即可，也就是让其中一个根指向另一个根，就使得两棵树合并成了一棵树，也就把两个组合并为了一个组。

查询

当我们要查询两个元素是否属于同一个组时，我们需要沿着各个节点往上向树的根进行查询，如果最终发现两个元素的根相同，那么他们就属于同一个组。反之，则不属于同一个组。

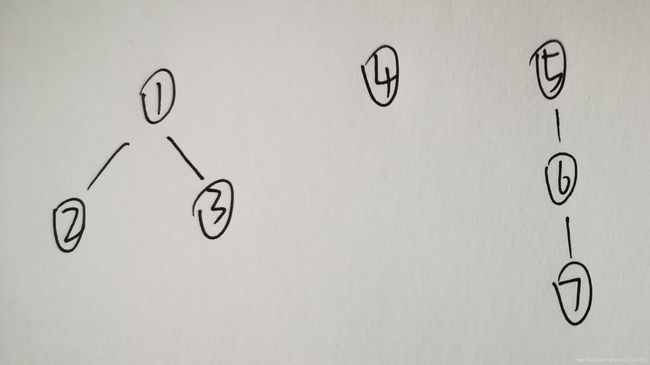
如图中：元素2和3的根都为元素1，故他们属于同一个组；元素2和7，他们的根分别为元素1和5，不同，故他们不属于同一个组。

代码实现

int f[maxn]; //全名为 father，父节点的意思

//初始化 n个元素 
void Init() {
	//使每个元素的根节点是其本身
	//即初始时每个元素都是单独的 
	for(int i=1; i<=n; i++) f[i]=i;  
}

//查询树的根
//非递归实现
int Find(int i) {
	while(f[i] != i) {  //直到元素的父节点是它本身，表示已经查询到了树的根
		i = f[i];
	return i; 			//返回根节点对应的元素 
}

//递归实现
int Find(int i) {
	if(f[i]==i)      //若元素的根节点为其本身，那么此元素就是树的根 
		return f[i];    //直接返回元素本身即可
	else
		return Find(f[i]); //否则继续查询，知道查询到树的根位置 
}

//简化版
int Find(int i) {
	return f[i]==i ? f[i] : Find(f[i]);
} 

//合并
void merge(int a, int b) {
	//先找到两个元素对应的根对应的元素 
	int fa = Find(a); 
	int fb = Find(b);
	if(fa==fb) return;
	else f[fa]=fb;  //否则令元素 a的根指向元素 b的根 
} 

//简化版
void merge(int a, int b) {
	f[Find(a)] = Find(b);
} 

优化1：避免退化（按秩合并）

因为并查集的结构是树状结构，所以需注意退化问题。避免退化发生的方法如下：
首先，我们合并时，可记录这棵树的高度（记为rank）。接下来当我们需合并两棵树时，我们先对两棵树的高度进行判断，如不同，则让高度小的树的根指向高度大的根。如下图：

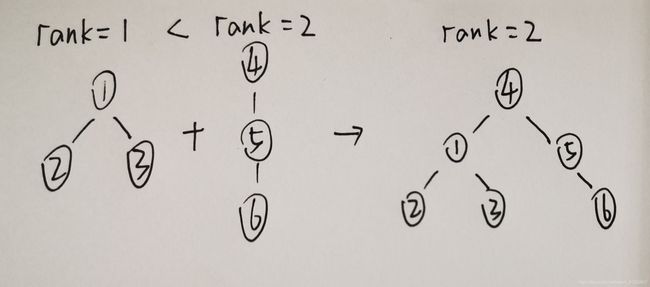
代码优化

对初始化(Init)函数和合并(merge)函数进行优化

//初始化优化
int f[maxn];
int h[maxn]; //全名为 height

void Init() {
	for(int i=1; i<=n; i++) {
		f[i] = i;
		h[i] = 0;  //令每棵树的高度初始值都为 0 
	}
} 

//合并优化
void merge(int a, int b) {
	int fa = Find(a);
	int fb = Find(b);
	if(fa==fb) return; 
	
	if(h[fa] < h[fb]) {  //如果元素 a对应的树的高度比 b小 
		f[fa] = fb;  //使元素 a的根指向元素 b的根 
	} else {
		f[fb] = fa;  //否则让元素 b的根指向元素 a的根 
		if(h[fa] == h[fb]) h[fa]++;
		// 如果两者对应的树的高度相同，则使新生成的树高度 +1 
	}
}

PTA L2-024 部落 (25 分)
在这题中，若不对merge进行优化就会运行超时

优化2：路径压缩

由于查询时我们需沿着元素所在的树从下往上查询，最终找到这棵树的根，表明这个元素与其根对应元素属于同一组。因为在此查询过程中我们会经过许多节点，而如果我们能将这个元素直接指向根节点，那么就能节省许多查询的时间。同时，在查询过程中，每次经过的节点，我们都可以同时将他们一起直接指向根节点。这样做的话，我们再查询这些节点时，就能很快知道他们的根是谁了。

代码优化

对查询(Find)函数进行优化

//查询优化
int Find(int i) {
	return f[i]==i ? f[i] : f[i] = Find(f[i]);
	//使元素直接指向树的根 
} 

最终代码实现

void Init() {
	for(int i=0; i<=n; i++) {
		f[i] = i;
		h[i] = 0;
	}
}
int Find(int i) {
	return f[i]==i ? f[i] : f[i]=Find(f[i]);
}
void merge(int a, int b) {
	int fa = Find(a);
	int fb = Find(b);
	if(fa != fb) {
		if(h[fa] < h[fb]) {
			f[fa] = fb;
		} else {
			f[fb] = fa;
			if(h[fa] == h[fb]) h[fa]++;
		}
	}
}

复杂度分析

经过两个优化后，并查集的效率变得非常高。对n个元素的并查集进行一次操作的均摊复杂度是O(a(n)) （a(n)是阿克曼函数的反函数），比优化前的O(log(n))还要快。

经典例题

并查集入门

Wireless_Network

并查集进阶1：带权并查集

带权并查集是什么？

带权是指一个元素具有额外的信息。比如元素1对应着数值6，元素2对应着数值4。这些带有信息的元素组成的并查集即为带权并查集。

带权并查集的作用是什么？

带权并查集能计算各个小组中元素的个数、能计算n个元素中还有几个元素没有加入小组中；计算分数、距离等等

注释：带权并查集需要在路径优化的基础下进行。

经典例题

The_Suspects

并查集进阶2：种类并查集

种类并查集是什么？

种类并查集是能把并查集分为几个部分，每个部分的种类不同。

种类并查集的作用是什么？

种类并查集能将两个阵容分开。比如把好人和坏人分为两个阵营。

经典例题

食物链

关押罪犯

参考资料：
《挑战程序设计竞赛》
路径压缩_并查集