Pytorch的grad、backward()、zero_grad()

grad 梯度

什么样的tensor有grad？

• pytorch中只有torch.float和复杂类型才能有grad。

x = torch.tensor([1, 2, 3, 4], requires_grad=True)

这里没有指定x的dtype=torch.float，那么是会报错的。
RuntimeError: Only Tensors of floating point and complex dtype can require gradients

• 正确的写法是：

x = torch.tensor(data=[1, 2, 3, 4], dtype=torch.float)

grad 的特点

• 如果x中的数据类型(dtype)是torch.tensor，那么requires_grad默认是True。
• 同时，默认grad=None，因为单单一个张量讲梯度是没有意义的。

backward() 反向传播

对于一个张量进行反向传播，会将所有与它关联的张量的梯度求解出来。
举个例子：
$$Y=W\times X$$
其中，W是一个1x4的矩阵，X是一个4x1的矩阵，那么Y就是一个1x1的矩阵。

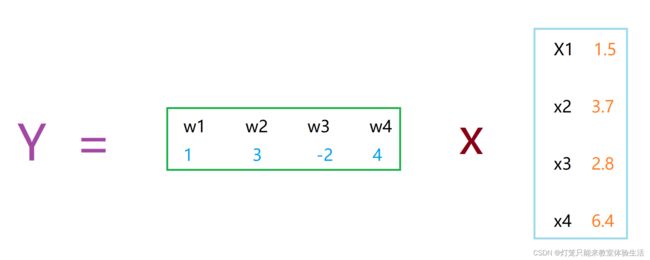
体现到代码中则是：

X = torch.tensor([[1.5],[3.7],[2.8],[6.4]], requires_grad=True, dtype=torch.float)
W = torch.tensor(data=[[1, 3, -2, 4]], requires_grad=True, dtype=torch.float)
Y = W.matmul(X)

>>>W
tensor([[ 1.,  3., -2.,  4.]], requires_grad=True)
>>>X
tensor([[1.5000],
        [3.7000],
        [2.8000],
        [6.4000]], requires_grad=True)
>>>Y
tensor([[32.6000]], grad_fn=\<MmBackward0>)

那么这个时候，梯度就是可以求的，对Y进行.backward()，会求出W与X的梯度。
$$Y=w_1\times x_1+w_2\times x_2+w_3\times x_3+w_4\times x_4$$
那么Y对x1求偏导，得到的就是w1，同理Y对xi求偏导得到wi；Y对wi求偏导得到xi。

• Y对xi求导时：其余的变量都固定，或者说其余的变量视为常量。
  $$\frac{\partial Y}{\partial x_i}=w_i$$

Y.backward()
>>>X.grad
tensor([[ 1.],
        [ 3.],
        [-2.],
        [ 4.]])
>>>W.grad
tensor([[1.5000, 3.7000, 2.8000, 6.4000]])

zero_grad() 清空梯度

为什么要清空梯度呢？

仍然拿上一个例子距离，我们再次执行Y.backward()，同时保证Y = W × X没有变化。

""""
必须设置为True，否则报错

RuntimeError: Trying to backward through the graph a second time 
(or directly access saved tensors after they have already been freed). 
Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). 
Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.

RuntimeError: 试图第二次向后遍历图（或者在它们已经被释放后直接访问保存的张量）。 
当您调用 .backward() 或 autograd.grad() 时，已保存的图形中间值被释放。 
如果您需要第二次向后遍历图形，或者如果您需要在向后调用后访问保存的张量，请指定 retain_graph=True。
"""
Y.backward(retain_graph=False)

>>>X = torch.tensor([[1.5],[3.7],[2.8],[6.4]], requires_grad=True, dtype=torch.float)
>>>W = torch.tensor(data=[[1, 3, -2, 4]], requires_grad=True, dtype=torch.float)
>>>Y = W.matmul(X)
>>>Y.backward(retain_graph=True)  # 保持计算图
>>>X.grad
tensor([[ 1.],
        [ 3.],
        [-2.],
        [ 4.]])
>>>Y.backward(retain_graph=True)
>>>X.grad
tensor([[ 2.],
        [ 6.],
        [-4.],
        [ 8.]])
>>>Y.backward(retain_graph=True)
>>>X.grad
tensor([[ 3.],
        [ 9.],
        [-6.],
        [12.]])

可以看到，每次反向传播求梯度时，都会加上上一次的梯度，但是没有改变W和X，梯度也不应该变化

手动清空梯度

torch.tensor.grad.zero_()

import torch

X = torch.tensor([[1.5],[3.7],[2.8],[6.4]], requires_grad=True, dtype=torch.float)
W = torch.tensor(data=[[1, 3, -2, 4]], requires_grad=True, dtype=torch.float)
Y = W.matmul(X)

Y.backward(retain_graph=True)
print(X.grad)
"""
tensor([[ 1.],
        [ 3.],
        [-2.],
        [ 4.]])
"""

Y.backward(retain_graph=True)
print(X.grad)
"""
tensor([[ 2.],
        [ 6.],
        [-4.],
        [ 8.]])
"""


Y.backward(retain_graph=True)
print(X.grad)
"""
tensor([[ 3.],
        [ 9.],
        [-6.],
        [12.]])
"""

X.grad.zero_()
print(X.grad)
"""
tensor([[0.],
        [0.],
        [0.],
        [0.]])
"""


Y.backward()
print(X.grad)
"""
tensor([[ 1.],
        [ 3.],
        [-2.],
        [ 4.]])
"""