强化学习笔记

深度强化学习要点摘要

扩展资料

交叉熵：

https://blog.csdn.net/qq_38846606/article/details/111929038

https://zhuanlan.zhihu.com/p/149186719

强化学习：

https://datawhalechina.github.io/easy-rl/

https://www.bilibili.com/video/BV1UE411G78S

机器学习中梯度的意义 偏导$\frac{\partial f}{\partial \theta }$代表了通过调整函数$f$的参数$\theta$向梯度上升或者下降的方向移动，从而达到$f$的极值。被偏导的函数是被优化的对象。

Overview

强化学习的整个过程由几个部分构成：

• Agent：是用来代替人的自动化的决策系统。
• Environment：Agent的交互对象，比如，围棋游戏。
• Action：Agent对Environment的操作，比如，在围棋中落子。
• State（Observation）：Agent的输入之一，代表了Agent对当前Environment的观察（是Environment的建模），Agent一般根据State来决定下一步的Action。
• Reward：Environment的输出，代表在根据特定State执行特定Action之后，是不是达成了需要的目标，比如，在围棋中落完子之后整盘棋是不是赢得了胜利（或失败）。

episode Agent与Environment互动过程的结束，比如，一盘围棋的结束。强化学习的过程就是要学习如何最大化在每次episode的时候的预期累计reward。

reward delay 强化学习的难点之一。reward delay有两种情况。1）对于有些场景，当Agent做出Action之后，并不是总是可以立刻得到Reward。比如围棋，在episode之前是无法知道棋局的胜负的，Environment在次期间给出的Reward都是0。也就是说在最终的结果出来之前，Agent需要在没有Reward的情况下给出Action。2）有时立刻给出Reward会使得Agent决策时目光短浅，所以刻意增加reward delay可以使Agent在做出Action时有更长远的考虑。

exploration 强化学习的难点之一。有时Agent的行为会影响到它之后从Environment看到的情况，所以Agent要有意地尝试不同的行为来对Environment进行充分的探索。

randomness in the environment 有时环境的变化和Action的作用没有关系，那么我们可以认为这是来自于环境中的随机性。

policy-based与value-based 两种强化学习的分支，前者训练一个做事的Actor，后者训练一个Critic。Critic不做任何事情，它对Actor行为进行批评。这两种方式可以结合。

policy-based approach

Actor policy-based approach的训练对象，是在Agent中的一个模型，用$\pi$表示。其以对于环境的Observation为输入，得到Action，内部的参数为$\theta$。最终可以表达为${\pi }_{\theta }(Observation)=Action$。在深度强化学习中，Actor中的模型是一个神经网络。Observation会将Environment建模为一个矩阵或者一个向量，输出是某个Action被采用的可能性。

Total Reward 设在第t轮决策中，Actor根据Observation $s_t$做出Action $a_t$，Environment根据$a_t$给出对应的$r_t$。那么假设到episode一共经历了$T$轮，那么Total Reward$R_{\theta }={\sum }_{t=0}^T{r}_t$（$\theta$是Actor中模型的参数）。而因为Environment中的随机性，所以整个流程会执行多次来获得Total Reward的期望$\overline{R_{\theta }}$。Actor的训练过程就是通过调整$\theta$来最大化$\overline{R_{\theta }}$。

$\overline{R_{\theta }}$的表达：

梯度上升的过程，需要对神经网络参数$\theta$求偏导：

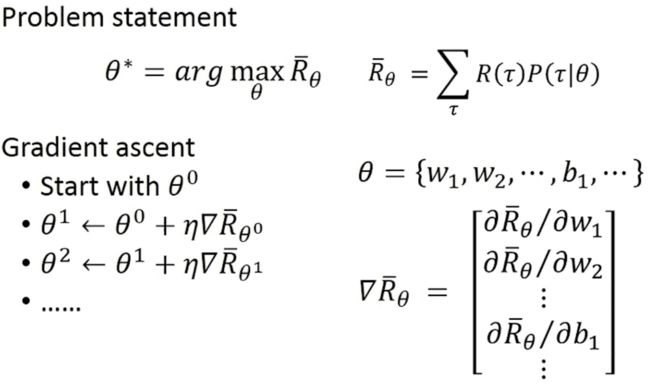
偏导的前一项是和参数$\theta$无关，只有概率$P$内部存在，通过在分子分母乘上同一个$P$，然后根据函数的微分规则导出log项，然后用多出来的$P$离散化为具体的多次episode的平均：

根据条件概率性质，将$P$拆开，具体为一系列小事件的概率相乘，其中$p(r_1,s_2|s_1,a_1)$，代表在Agent给出Action $a_1$之后，环境由$s_1$变为$s_2$，并且给出Reward $r_1$的概率。其中$p(a_1|s_1,\theta )$，代表在Agent在参数$\theta$的模型中根据$s_1$给出$a_1$的概率。前者完全Environment决定，是个未知的黑盒（这是符合实际的），后者是Actor的模型控制的：

按照前面求偏导的要求，最等式左边求log（右边少了一个括号），最终得到偏导项的计算方法，而这一偏导项用以更新$\theta$：

可以用交叉熵来解释式子的后半程，$\nabla logp(a_t^n|s_t^n,\theta )$，其本质代表在序列的$t$时刻Actor在参数$\theta$下的可能决策的概率与实际决策的交叉熵的梯度。交叉熵的原始定义是$-{\sum }_{a\in allaction,s\in allstate}q(a|s)logp(a|s,\theta )$。其中$q$是模型实际的决策（也就是选择概率最高的$a|s$）所对应的各个$a|s$事件的概率，在这个例子中$q$仅有$q(a_t|s_t)$是1，其他都是0，是个one-hot。所以$\sum$符号可以消除掉，简化为$-q(a_t|s_t)logp(a_t|s_t,\theta )$，并最终简化为$-logp(a_t|s_t,\theta )$。在这里，交叉熵是一个loss函数，代表了一个决策$a|s$在模型中产生的概率和模型实际决策的概率的距离（相似度），而做梯度下降的方向就是$-\nabla logp(a_t|s_t,\theta )$，代表如果让模型更倾向于做出$a_t|s_t$的决策，参数$\theta$要做出的变化。

$-{\sum }_{t=1}^T\nabla logp(a_t|s_t,\theta )$代表了在一个序列中（一次episode之前）每一个时间点的决策的概率与它们实际做出决策所对应的概率的总交叉熵下降的方向。而它们又于当前序列的Reward $R(\tau )$相乘，可以解释为如果当前决策Reward是负的，说明当前决策所代表的不是真理，方向是错误，那么就要远离这个方向，反之也一样。$R(\tau )$这个参数的作用就是根据环境给出的总奖励来调整参数，让决策$a|s$更靠近或者远离其尝试的方向。

$-{\sum }_{t=1}^T\nabla logp(a_t|s_t,\theta )$前面有一个负号，但是上面推导的结果没有是因为负负得正。

Baseline 当所有Action的Reward都是正的，所以只要这个Action被尝试过，不管效果好不好，模型肯定会往这个方向梯度上升，这会导致在学习过程中被尝试或者大量尝试的action会有更大的可能性被选中，不利于选出效果好的Action。所以可以要给奖励一个减一个baseline，给被尝试得比较少的Action一些被选择的机会，并且减少Reward不高的Action被选择的概率。

Implementation 在实际的实现中，几乎可以把一个离散的Policy-based的训练问题当成一个输出为Softmax形式的分类问题的训练，输入是State $s$，而输出是一个类别，也是一个Action $a$。而分类的损失函数（最终其实就是信息熵）计算，是在Actor实际执行的Action $a$作为分类训练的label与模型实际输出的向量（每种选择的概率）之间进行。只是说要对损失函数进行一点点修改，加一个$R({\tau }^n)$来为分类器的梯度下降额外加一个权重。

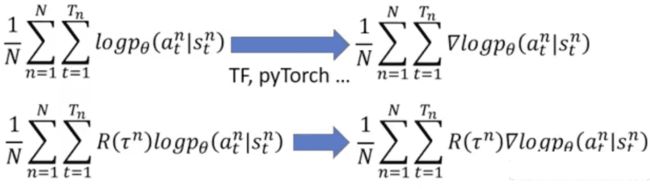
Advantage function 使用Total Reward来作为某一个Action是不是好的Action的权重有时候并不总是最正确的。这里权重的表达是可以泛化到”当前的Action相比其他的Action要好多少“这一问题上的，用$A^{\theta }(s_t,a_t)$表示。$A^{\theta }(s_t,a_t)=R({\tau }^n)$可能会让滥竽充数的Action也获得不错的Reward，这就不客观了。所以有一些改进的方法，比如$A^{\theta }={\sum }_{t^{\prime }=t}^{T_n}{r}_{t^{\prime }}^n$，仅仅将这个Action执行之后的所有Reward作为这个Action的权重，比如$A^{\theta }={\sum }_{t^{\prime }=t}^{T_n}{r}_{t^{\prime }}^n{\gamma }^{t^{\prime }-t}(\gamma <1)$，在前面一种执行方法的基础上降低更远的Reward的影响，因为在一个Action对他之后更远Reward贡献更少。

Critic

Critic并不实际做出任何决定，而是用一个模型来判断Actor做得好不好，可以大概表达为$V^{\pi }(s)$，是当前Actor在State $s$下最终可以获得的total reward。

Monte-Carlo based approach 这类Critic会观察Actor的行为，并且在序列中，拟合每一个State $s$和序列最终获得的Total Reward之间的关系。

Temporal-difference approach 有时候，整个序列很长，会降低Critic的训练效率，所以Critic不使用Total Reward来训练，而是将某次$r_t$作为两个相邻State在特定Actor所分别对应的Total Reward的差值来进行训练。即让Critic的$V^{\pi }(s_{t+1})-V^{\pi }(s_t)$与$r_t$拟合在一起。

Q function 拟合Actor $\pi$在State $s$下做出Action $a$的Total Reward预期。也可以表达为拟合$Q^{\pi }(s,a)$与Total Reward之间的关系。这个Critic在$a$是离散的时候意义很大，可以指导Actor的工作。我们可以再特定的$s$下选出$Q^{\pi }(s,a)$最大的$a$，作为Actor的决策。

Q-learning 在Action是离散的时候的一种改进。初始存在一个Actor $\pi$通过Monte-Carlo或者Temporal-difference的方法训练出它对应的Q function $Q^{\pi }(s,a)$，通过找到$Q^{\pi }(s,a)$中每一个$s$对应的最佳$a$来构造更优的Actor ${\pi }^{\prime }$。这个过程可以简洁地表达为${\pi }^{\prime }(s)=argma{x}_a{Q}^{\pi }(s,a)$。而通过Q-learning产生的Actor没有参数，它仅仅包含了Q function并且枚举Action。“https://arxiv.org/pdf/1710.02298.pdf”有更多的细节。

Actor-Critic

一般的Actor使用Total Reward来做修改$\theta$，使得Total Reward可以尽可能大。在Policy-based的方法中，Total Reward是一个参数来调整$\theta$，使得Actor更接近或者更远离其既定的决策方向（Reward大就更接近已有的决策，Reward小就远离已有的决策）。但是，$R(\tau )$的随机性是很高的，直接基于Actor的互动过程去学可能效果不好，所以有一种方法是使用Critic预估出来的Reward来计算这里的权重。这里的方法有很多，比如：
$$r_t^n-(V^{\pi }(s_t^n)-V^{\pi }(s_{t+1}^n))$$
这个式子会被嵌到Policy-based approach的$R({\tau }^n)$的位置。这个权重表达的意思很清晰，后面一项是Critic对Actor当前Action的Reward的预测：$V^{\pi }(s_t^n)-V^{\pi }(s_{t+1}^n)$。$r_t^n$是实际的当前reward。产生的效果是，如果实际的reward更大，那就说明Actor对于当前决策的重视程度不够，这个权重是正的，增加Actor执行这一Action的概率。如果这个权重是相等的或者更小，那么不变或者减少对应Action的概率。

asynchronous 异步训练，开多台机器同时并行训练。然后用分别产生的Reward更新同一个模型，总而达成更高效的训练。

Proximal Policy Optimization

on-policy 使用Actor $\pi$来生成Reward并更新$\pi$的参数$\theta$被称为on-policy。这种方式的缺点在于一旦$\theta$在经过一轮更新之后，老版本的Actor与Environment的记录没有办法用来改良新的Actor。

off-policy 根据概率分布的定义，可以用不同概率分布的比例来在不同概率分布下的做函数期望的装换，这种技术叫做importance sampling：

在这里$x$本来在概率分布$p$中做采样并且来求$f(x)$的期望。但是通过在积分中做出变换，我们可以让$x$在$q$中采样，通过求$f(x)\frac{p(x)}{q(x)}$来“迂回”求出在$p$分布中$f(x)$的期望。如果在这里将$f(x)$换成强化学习Reward或者Advantage Function的梯度，把$p(x)$和$q(x)$视为新的Actor $\pi$和老的Actor ${\pi }^{\prime }$所做出Action的概率分布，那么我们就可以让$\pi ’$与Environment互动的历史数据应用在$\pi$的训练中。最终Reward的定义可以变为：

然后将$\tau$和$p(\tau )$展开到Action和State的粒度。这个式子可以不严格地推导为：

最终达成的效果是，使用老的Actor的Advantage Function的$A^{{\theta }^{\prime }}$乘上新老Actor的策略的概率分布的比例$\frac{p_{\theta }(s_t|a_t)}{p_{{\theta }^{\prime }}(s_t|a_t)}$，和老的Actor的执行历史$(s_t,a_t){\pi }_{{\theta }^{\prime }}$来求新的Actor的梯度，从而更新新的Actor的参数。

off-policy最终产生的好处是，通过on-policy产生的Actor可以用off-policy的方式再进一步优化，从而很好地复用旧Actor的历史数据，增加训练的效率。

这个导函数的原目标函数（是加了权重的Advantage function、被优化的函数，要通过调整$\theta$的取值是的这个目标函数够大）为：

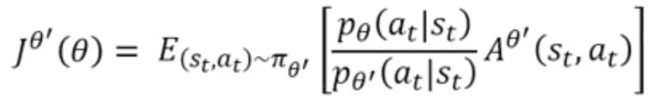
off-policy的局限 importance sampling保证了在新的$x$的分布下$f(x)$期望的新计算方法，但是等式两边的是期望的相等，而不是分布的相等。期望只有在足够多的sampling之后才能通过求平均才能得到，当sampling不够多时，平均值与期望是有偏差的，特别是$p(x)$和$q(x)$差别很大时。所以，为了让来自旧Actor的历史数据能在接下来的也可以使用，需要再增加带权重的Advantage Function的同时也需要降低off-policy中新Actor和老Actor之间的差距，所以$j^{{\theta }^{\prime }}(\theta )$后面还可以加一项表达二者差距的函数。比如KL散度（$\beta$是KL散度的权重）：

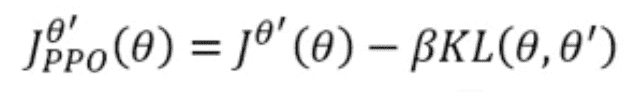
这里的KL散度表达了参数分别为$\theta$和${\theta }^{\prime }$的新旧Actor的做出Action的概率分布的区别大小。这一项是需要往小的方向优化的，所以前面是符号。当然有其他各种方法来表达新旧Actor的区别，比如PPO2中的clip函数。